Phương pháp giải Cách xác định góc tạo bởi một đường thẳng cắt hai đường thẳng (50 bài tập minh họa)

Ngọc Nguyễn Ngày: 15-07-2023 Lớp 7

360

Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Cách xác định góc tạo bởi một đường thẳng cắt hai đường thẳng (50 bài tập minh họa) hay, chi tiết nhất, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về hỗn số, từ đó học tốt môn Toán 7.

Phương pháp giải Cách xác định góc tạo bởi một đường thẳng cắt hai đường thẳng (50 bài tập minh họa)

I. LÝ THUYẾT:

Cho đường thẳng c cắt đường thẳng a và b lần lượt tại điểm A và B (như hình vẽ).

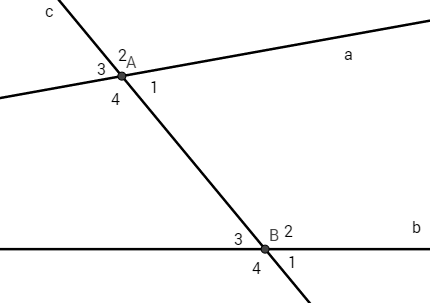
Phương pháp giải Cách xác định góc tạo bởi một đường thẳng cắt hai đường thẳng (50 bài tập minh họa) (ảnh 1)

1. Hai cặp góc so le trong:

$\hat{A_{1}}$ và $\hat{B_{3}};$ $\hat{A_{4}}$ và $\hat{B_{2}} .$

2. Bốn cặp góc đồng vị:

$\hat{A_{1}}$ và $\hat{B_{1}};$ $\hat{A_{2}}$ và $\hat{B_{2}};$

$\hat{A_{3}}$ và $\hat{B_{3}};$ $\hat{A_{4}}$ và $\hat{B_{4} .}$

3. Hai cặp góc trong cùng phía:

$\hat{A_{1}}$ và $\hat{B_{2}};$ $\hat{A_{4}}$ và $\hat{B_{3} .}$

4. Quan hệ giữa các cặp góc:

Nếu hai đường thẳng cắt một đường thẳng thứ ba và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:

- Hai góc so le trong còn lại bằng nhau.

- Hai góc đồng vị bằng nhau.

II. CÁC DẠNG BÀI TẬP CƠ BẢN:

Dạng 3.1: Vẽ hình và tìm cặp góc so le trong, cặp góc đồng vị, cặp góc trong cùng phía.

1. Phương pháp giải: Nhận biết hai góc trong một cặp dựa vào tên của cặp góc căn cứ vào vị trí của góc so với hai đường thẳng và đường thẳng thứ ba.

2. Ví dụ minh họa:

Ví dụ 1: Cho hình vẽ.

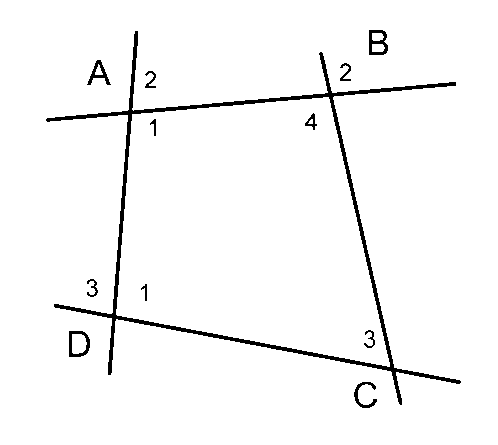
Tài liệu VietJack

a) Kể tên các góc so le trong với ${\hat{A}}_{2} ?$

b) Kể tên các góc trong cùng phía với ${\hat{C}}_{3} ?$

c) Góc kề bù với ${\hat{A}}_{1}$ góc nào?

d) Góc đồng vị với ${\hat{A}}_{2}$ góc nào?

e) Nếu ${\hat{A}}_{2} = {\hat{B}}_{2}$ thì mối quan hệ giữa ${\hat{B}}_{4}$ và ${\hat{A}}_{1}$ là gì?

Giải:

a) Góc so le trong với ${\hat{A}}_{2}$ là ${\hat{B}}_{4} .$

b) Góc trong cùng phía với ${\hat{C}}_{3}$ là ${\hat{D}}_{1}; {\hat{B}}_{4} .$

c) Góc kề bù với ${\hat{A}}_{1}$ là ${\hat{A}}_{2}$ .

d) Góc đồng vị với ${\hat{A}}_{2}$ là ${\hat{D}}_{1}; {\hat{B}}_{2}$ .

e) Vì ${\hat{A}}_{1}$ kề bù với ${\hat{A}}_{2}$ nên ${\hat{A}}_{1} + {\hat{A}}_{2} = 180^{o}$ (1)

Ta có: ${\hat{B}}_{2} = {\hat{B}}_{4}$ (đối đỉnh) (2)

Theo đề bài, ${\hat{A}}_{2} = {\hat{B}}_{2}$ (3)

Từ (1), (2) và (3) ta suy ra ${\hat{A}}_{1} + {\hat{B}}_{4} = 180^{o}$ .

Dạng 3.2: Tính số đo các góc khi biết một trong bốn góc tạo bởi hai đường thẳng.

1. Phương pháp giải:

Áp dụng tính chất của hai góc đối đỉnh, hai góc kề bù, hai góc so le trong, hai góc đồng vị để tính góc.

2. Ví dụ minh họa:

Ví dụ 2: Cho hình vẽ. Giả sử $\hat{y B A} = \hat{B A x'} = 105^{o}$ .

Tính số đo các góc $\hat{z' B y'}; \hat{x A B}$ ?

Tài liệu VietJack

Giải:

Vì $\hat{y B A} = \hat{B A x'} = 105^{o}$ (hai góc này ở vị trí so le trong).

Ta có: $\hat{z' B y'} = \hat{y B A}$ (đối đỉnh)

Mặt khác: $\hat{x A B} + \hat{BAx'} = \hat{xAx'} = 180^{o}$

Vậy $\hat{z' B y'} = 105^{o}; \hat{x A B} = 75^{o} .$

Dạng 3.3: Tìm các cặp góc bằng nhau, các cặp góc bù nhau.

1. Phương pháp giải:

Sử dụng quan hệ giữa các cặp góc so le trong, đồng vị, trong cùng phía.

2. Ví dụ minh họa:

Ví dụ 3: Cho hình bên trong đó

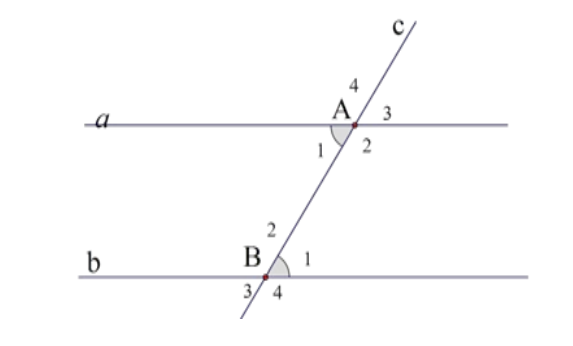
Tài liệu VietJack

Tìm quan hệ giữa:

a) ${\hat{A}}_{3}$ và ${\hat{B}}_{3}$

b) ${\hat{A}}_{4}$ và ${\hat{B}}_{2}$

c) ${\hat{A}}_{3}$ và ${\hat{B}}_{2}$

Giải:

a) Ta có ${\hat{A}}_{1} = {\hat{A}}_{3}$ (đối đỉnh); ${\hat{B}}_{1} = {\hat{B}}_{3}$ (đối đỉnh)

Mà theo đề bài, ${\hat{A}}_{1} = {\hat{B}}_{1} .$

Do đó ${\hat{A}}_{3} = {\hat{B}}_{3} .$

b) ${\hat{A}}_{4}$ và ${\hat{B}}_{2}$

Ta có ${\hat{A}}_{4} + {\hat{A}}_{1} = 180^{o}$ ; ${\hat{B}}_{2} + {\hat{B}}_{1} = 180^{o}$

Mà theo đề bài, ${\hat{A}}_{1} = {\hat{B}}_{1} .$

Do đó ${\hat{A}}_{4} = {\hat{B}}_{2} .$

c) ${\hat{A}}_{3}$ và ${\hat{B}}_{2}$

Ta có ${\hat{A}}_{3} + {\hat{A}}_{4} = 180^{o};$ ${\hat{A}}_{4} = {\hat{B}}_{2}$ (câu b)

Do đó ${\hat{A}}_{3} + {\hat{B}}_{2} = 180^{o} .$

III. BÀI TẬP VẬN DỤNG:

Bài 1: Cho hình vẽ bên dưới, chọn đáp án đúng:

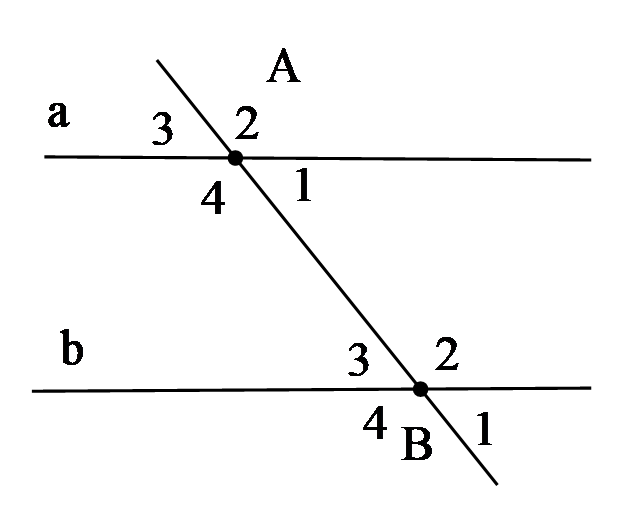
Tài liệu VietJack

A. ${\hat{A}}_{1}$ và ${\hat{B}}_{2}$ là hai góc so le trong.

B. ${\hat{A}}_{2}$ và ${\hat{B}}_{2}$ là hai góc trong cùng phía.

C. ${\hat{A}}_{2}$ và ${\hat{B}}_{3}$ là hai góc đồng vị.

D. ${\hat{A}}_{4}$ và ${\hat{B}}_{3}$ là hai góc trong cùng phía.

Bài 2: Cho hình vẽ sau:

Tài liệu VietJack

Hai góc được đánh dấu trên hình ở vị trí nào:

A. So le trong.

B. Trong cùng phía.

C. Kề bù.

D. Đồng vị.

Bài 3: Cho hình vẽ sau:

Tài liệu VietJack

a. Kể tên 2 cặp góc ở vị trí so le trong.

b. Kể tên 3 cặp góc ở vị trí trong cùng phía.

Bài 4: Ở miền trong của góc tù vẽ các tia OC, OD sao cho . Chứng minh rằng

Bài 5: Cho đường thẳng cắt hai đường thẳng khác như hình vẽ. Xác định các cặp góc so le trong, đồng vị.

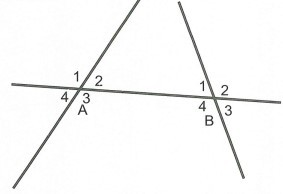
Tài liệu VietJack

Bài 6: Cho hình vẽ:

Tài liệu VietJack

Xác định số đo của các góc còn lại.

Bài 7: Chứng tỏ rằng hai tia phân giác của hai góc kề bù tạo thành một góc vuông.

Bài 8: Vẽ hình theo cách diễn đạt bằng lời sau:

a. Vẽ $\hat{A O B} = 50^{O} .$ Lấy điểm C bất kì nằm trong $\hat{A O B} .$ Qua C vẽ đường thẳng m vuông góc với OB và đường thẳng n song song với OA.

b. Cho $\hat{x O y} = 65^{O} .$ Lấy điểm M bất kì nằm trong $\hat{x O y} .$ Vẽ $M A ⊥ O x$ $(A \in Ox)$ ; $A B ⊥ O y (B \in O y)$ . Vẽ đường thẳng d qua điểm M và song song với Oy.

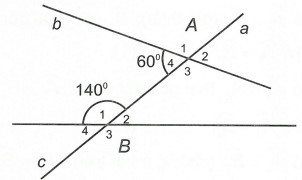
Bài 9: Cho hình vẽ sau:

Tài liệu VietJack

Giả sử ${\hat{A}}_{1} = {\hat{B}}_{3}$ . Tính số đo các góc tại A và B, biết: ${\hat{B}}_{2} = 4 {\hat{A}}_{1}$

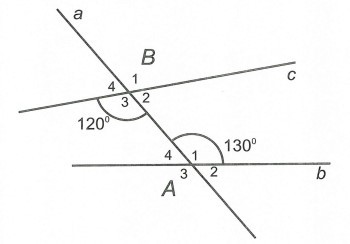
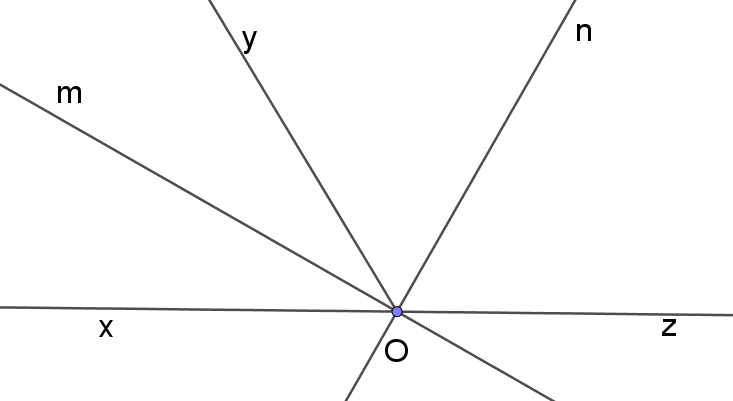
Bài 10: Cho đường thẳng a cắt hai đường thẳng b, c như hình vẽ.

a) Nêu tên những cặp góc so le trong, những cặp góc đồng vị.

b) Biết ${\hat{A}}_{1} = 130^{o}$ và ${\hat{B}}_{3} = 120^{o},$ hãy tính các góc còn lại.

Tài liệu VietJack

Hướng dẫn giải:

Bài 1: Đáp án: D.

Bài 2: Đáp án: D.

Bài 3:

a) $\hat{B D C}$ và $\hat{A B D}$ ; $\hat{A D B}$ và $\hat{D B C}$

b) $\hat{A D C}$ và $\hat{D C B}$ ; $\hat{D C B}$ và $\hat{C B A}$ ; $\hat{B A D}$ và $\hat{A D C}$

Bài 4:

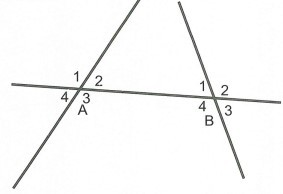
Tài liệu VietJack

$O C ⊥ O A \Rightarrow \hat{A O C} = 90^{0}$ , $O D ⊥ O B \Rightarrow \hat{D O B} = 90^{0}$

$\hat{A O D} = \hat{B O C} = \hat{A O B} - 90^{0} .$

Bài 5:

Tài liệu VietJack

Các cặp góc so le trong là ${\hat{A}}_{3}$ và ${\hat{B}}_{1}$ ; ${\hat{A}}_{2}$ và ${\hat{B}}_{4}$

Các cặp góc đồng vị là ${\hat{A}}_{1}$ và ${\hat{B}}_{1}$ ; ${\hat{A}}_{2}$ và ${\hat{B}}_{2}$ ; ${\hat{A}}_{3}$ và ${\hat{B}}_{3}$ ; ${\hat{A}}_{4}$ và ${\hat{B}}_{4}$ .

Bài 6:

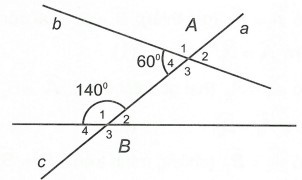
Tài liệu VietJack

Ta có: ${\hat{A}}_{2} = {\hat{A}}_{4} = 60^{o}$ (hai góc đối đỉnh)

$\Rightarrow {\hat{A}}_{1} = {\hat{A}}_{3} = 180^{o} - 60^{o} = 120^{o}$

${\hat{B}}_{1} = {\hat{B}}_{3} = 140^{o}$ (hai góc đối đỉnh)

$\Rightarrow {\hat{B}}_{2} = {\hat{B}}_{4} = 180^{o} - 140^{o} = 40^{o}$

Bài 7:

Tài liệu VietJack

Xét hai góc kề bù $\hat{x O y}$ và $\hat{y O z}$ có:

Om, On lần lượt là tia phân giác của hai góc trên nên.

$\hat{m O n} = \hat{m O y} + \hat{y O n} = \frac{1}{2} (\hat{x O y} + \hat{y O z}) = 90^{o}$ .

Bài 8:

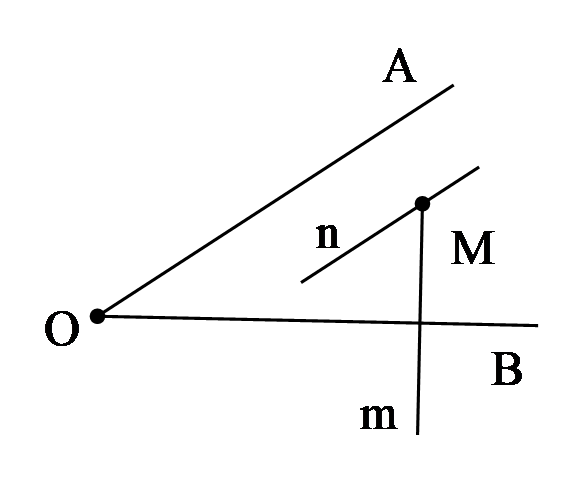
Tài liệu VietJack

Bài 9:

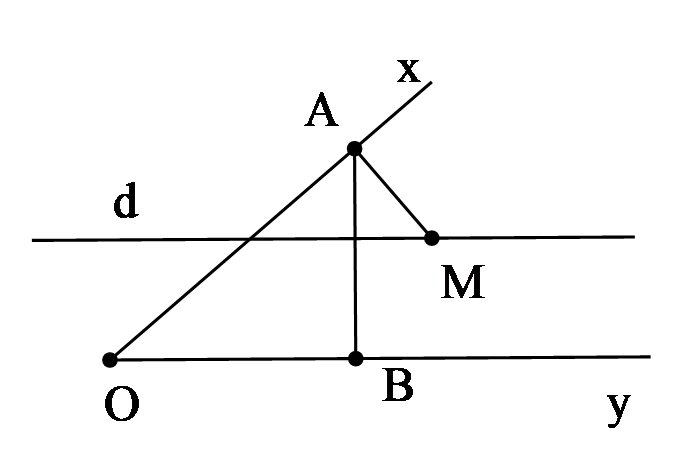
Tài liệu VietJack

Ta có: ${\hat{A}}_{1} = {\hat{B}}_{3} \Rightarrow {\hat{A}}_{1} = {\hat{B}}_{1}; {\hat{A}}_{4} = {\hat{B}}_{2}$

Mặt khác $\hat{4 A_{1}} = \hat{B_{2}} \Rightarrow 4 \hat{B_{3}} = \hat{B_{2}}$ và $\hat{B_{3}} + \hat{B_{2}} = 180^{0}$

Từ đó tính được

${\hat{A}}_{1} = {\hat{A}}_{3} = {\hat{B}}_{1} = {\hat{B}}_{3} = 180^{o} : (4 + 1) = 36^{o}$

${\hat{A}}_{2} = {\hat{A}}_{4} = {\hat{B}}_{2} = {\hat{B}}_{4} = 36^{o} .4 = 144^{o}$

Bài 10:

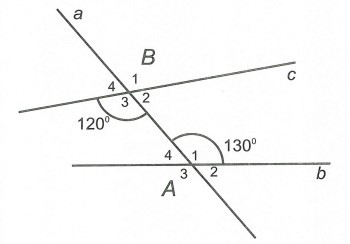
Tài liệu VietJack

a) Các cặp góc so le trong: ${\hat{A}}_{1}$ và ${\hat{B}}_{3};$ ${\hat{A}}_{4}$ và ${\hat{B}}_{2}$ .

Các cặp góc đồng vị là ${\hat{A}}_{1}$ và $\hat{B_{1}}$ ; ${\hat{A}}_{2}$ và ${\hat{B}}_{2}$ ; ${\hat{A}}_{3}$ và ${\hat{B}}_{3}$ ; ${\hat{A}}_{4}$ và ${\hat{B}}_{4} .$