Cho hàm số xác định trên , có đạo hàm trên và có bảng biến thiên như sau
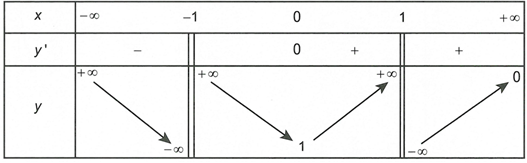
Đồ thị hàm số có bao nhiêu tiệm cận đứng và tiệm cận ngang?
A. 2
B. 3
C. 4
D. 5
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn đáp án C
Cho hàm số (C). Gọi M là điểm bất kỳ trên , d là tổng khoảng cách từ M đến hai đường tiệm cận của đồ thị. Giá trị nhỏ nhất của d bằng
Biết đồ thị hàm số nhận trục hoành và trục tung làm hai tiệm cận thì giá trị bằng
Cho hàm số y= f(x) có bảng biến thiên như sau
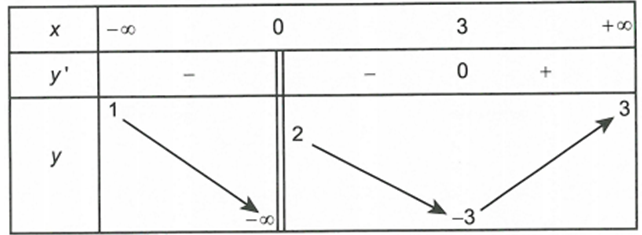
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
Tính tổng tất cả các giá trị nguyên của tham số m để đồ thị hàm số không có đường tiệm cận đứng
Cho hàm số y= f(x) liên tục trên R và có đồ thị như hình vẽ.
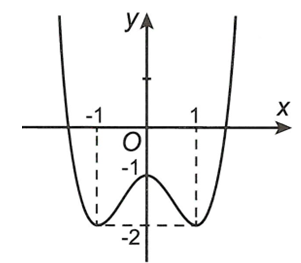
Số đường tiệm cận đứng của đồ thị hàm số là
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y=f(x) có bảng biến thiên như sau
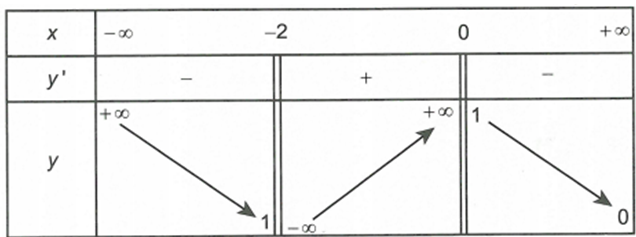
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số có hai tiệm cận đứng?
Cho hàm số bậc ba có đồ thị hàm số như hình vẽ bên dưới. Đồ thị hàm số có bao nhiêu tiệm cận đứng?
Gọi S là tập các giá trị nguyên dương của tham số m để đồ thị hàm số có ba tiệm cận. Tổng các giá trị của tập S bằng
Cho hàm số là hàm đa thức bậc 6 thỏa mãn và . Đồ thị hàm số như hình vẽ.
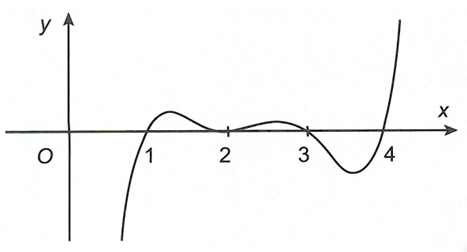
Số đường tiệm cận đứng của đồ thị hàm số là
Biết các đường tiệm cận của đường cong và trục tung cắt nhau tạo thành một đa giác . Mệnh đề nào dưới đây đúng?
Cho hàm số bậc bốn có đồ thị như hình vẽ bên. Số đường tiệm cận đứng của đồ thị hàm số
là
![Cho hàm số bậc bốn y=f(x) có đồ thị như hình vẽ bên. Số đường tiệm cận đứng của đồ thị hàm số y= (x^2-4)(x^2+2x)/ [f(x)]^2+2f(x)-3 là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid20-1674813184.png)
Tất cả các giá trị thực của tham số m để đồ thị hàm số có tiệm cận đứng nằm bên phải trục tung là
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.