Họ nguyên hàm của hàm số $f\left( x \right) = 2x + \frac{3}{{{x^2}}}$ là

Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ và $\int\limits_2^5 {f\left( x \right)dx = 2025}$. Tính $\int\limits_0^1 {f\left( {3x + 2} \right)} dx$.

Tại một nhà máy sản xuất một loại phân bón, gọi $P\left( x \right)$ là lợi nhuận (tính theo triệu đồng) thu được từ việc bán $x$ tấn sản phẩm trong một tuần. Khi đó, đạo hàm $P'\left( x \right)$, gọi là lợi nhuận cận biên, cho biết tốc độ tăng lợi nhuận theo lượng sản phẩm bán được. Giả sử lợi nhuận cận biên (tính theo triệu đồng/tấn) của nhà máy được ước lượng bởi công thức $P'\left( x \right) = 16 - 0,02x$ với $0 \le x \le 100$. Tính lợi nhuận (triệu đồng) nhà máy thu được khi bán 90 tấn sản phẩm trong tuần. Biết rằng nhà máy lỗ 25 triệu đồng nếu không bán được lượng sản phẩm nào trong tuần.

Cho đồ thị hàm số $y = {e^x}$ và hình được tô màu như dưới

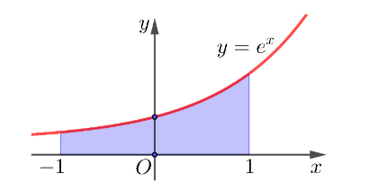
a) Hình phẳng được tô màu giới hạn bởi 3 đường.

b) Diện tích hình phẳng được tính bởi công thức $S = \int\limits_{ - 1}^1 {{{\left( {{e^x}} \right)}^2}dx}$.

c) Diện tích hình phẳng $S = e - \frac{1}{e}$.

d) Thể tích khối tròn xoay khi quay hình phẳng đó quanh trục $Ox$ là $V = \frac{1}{2}\pi \left( {{e^2} - \frac{1}{{{e^2}}}} \right)$.

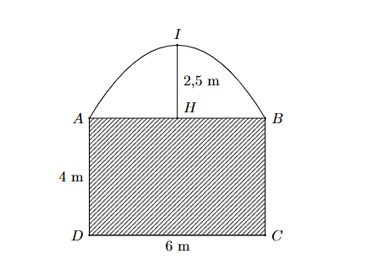
Một gia đình muốn làm cánh cổng (như hình vẽ). Phần phía trên cổng có hình dạng là một parabol với $IH = 2,5{\rm{m}}$, phần phía dưới là một hình chữ nhật kích thước cạnh là $AD = 4{\rm{m}}$, $AB = 6{\rm{m}}$. Giả sử giá để làm phần cổng được tô màu là 1000000 đồng/m² và giá để làm phần cổng phía trên là 1200000 đồng/m². Số tiền tổng cộng gia đình cần trả là bao nhiêu triệu đồng?

Trong một khung lưới ô vuông gồm các hình lập phương, người ta đưa ra một cách kiểm tra bốn nút lưới (đỉnh hình lập phương) bất kì có đồng phẳng hay không bằng cách gắn hệ trục toạ độ $Oxyz$ vào khung lưới ô vuông và lập phương trình mặt phẳng đi qua ba nút lưới trong bốn nút lưới đã cho. Giả sử có ba nút lưới mà toạ độ lần lượt là $\left( {1;1;10} \right)$, $\left( {4;3;1} \right)$,$\left( {3;2;5} \right)$ và mặt phẳng đi qua ba nút lưới đó có phương trình $x + my + nz + p = 0$. Giá trị của$m + n + p$ là bao nhiêu?

Cho hàm số $f\left( x \right)$ xác định trên $\mathbb{R}\backslash \left\{ 1 \right\}$ thỏa mãn $f'\left( x \right) = \frac{1}{{x - 1}},f\left( 0 \right) = 2,f\left( 4 \right) = 3$. Tính giá trị của biểu thức $f\left( { - 2} \right) + f\left( 2 \right)$.

Biết $F\left( x \right) = {x^3} - 3{x^2} + 2x$ là một nguyên hàm của hàm số $f\left( x \right)$ trên $\mathbb{R}$.

a) $F\left( 1 \right) = 0$.

b) $\int {F\left( x \right)dx} = 3{x^2} - 6x + 2$.

c) $f\left( x \right) = 3{x^2} - 6x + 2$.

d) Nếu $G\left( x \right)$ cũng là một nguyên hàm của hàm số $f\left( x \right)$ trên $\mathbb{R}$ thì $F\left( x \right) = G\left( x \right)$.

Trong không gian $Oxyz$, cho hai điểm $A\left( {2;4;1} \right),B\left( { - 1;1;3} \right)$ và mặt phẳng $\left( P \right):x - 3y + 2z - 5 = 0$. Mặt phẳng $\left( Q \right)$ đi qua $A,B$ và vuông góc với $\left( P \right)$ có phương trình dạng $ax + by + cz + 11 = 0$. Tính $a + b + c$.

Cho hình phẳng giới hạn bởi đồ thị của hàm số $y = f\left( x \right)$ liên tục và không âm trên đoạn $\left[ {1;3} \right]$, trục $Ox$ và hai đường thẳng $x = 1;x = 3$ quay quanh trục $Ox$, ta được khối tròn xoay. Thể tích của khối tròn xoay này được tính theo công thức nào dưới đây?

Cho $\int\limits_{ - 3}^0 {f\left( x \right)dx} = - 4$ và $\int\limits_{ - 3}^0 {g\left( x \right)dx} = - 3$.

a) $\int\limits_0^{ - 3} {f\left( x \right)dx} = - 4$.

b) $\int\limits_{ - 3}^0 { - 3f\left( x \right)dx} = 12$.

c) $\int\limits_{ - 3}^0 {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} = - 7$.

d) $\int\limits_{ - 3}^0 {\left[ {f\left( x \right) + 3x} \right]dx} = - 10$.

Trong không gian $Oxyz$, cho mặt phẳng $\left( P \right):3x + 2y - 4z + 1 = 0$.

a) $\overrightarrow n = \left( {3;2; - 4} \right)$ là một vectơ pháp tuyến của $\left( P \right)$.

b) $A\left( { - 1; - 1; - 1} \right)$ là một điểm nằm trên $\left( P \right)$.

c) Mặt phẳng $\left( Q \right)$ đi qua $B\left( {1;2;3} \right)$ và song song với mặt phẳng $\left( P \right)$ có phương trình là $3x + 2y - 4z + 5 = 0$.

d) $d\left( {\left( P \right),\left( Q \right)} \right) = d\left( {A,\left( Q \right)} \right) = 2$.