A. Nếu 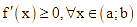 thì hàm số
thì hàm số ![]() đồng biến trên khoảng
đồng biến trên khoảng ![]() .
.
 Giải bởi Vietjack
Giải bởi Vietjack
Nếu 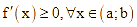 thì hàm số
thì hàm số ![]() chưa chắc đã đồng biến trên khoảng
chưa chắc đã đồng biến trên khoảng ![]() vì vẫn có thể xảy ra trường hợp
vì vẫn có thể xảy ra trường hợp 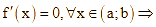 Mệnh đề 1 sai.
Mệnh đề 1 sai.
Điểm ![]() là điểm cực trị của hàm số
là điểm cực trị của hàm số ![]() nếu
nếu ![]() đổi dấu khi
đổi dấu khi ![]() đi qua
đi qua ![]() Mệnh đề 2 đúng.
Mệnh đề 2 đúng.
Hàm số ![]() luôn đồng biến trên
luôn đồng biến trên ![]() Mệnh đề 3 sai vì
Mệnh đề 3 sai vì ![]() luôn đồng biến trên
luôn đồng biến trên ![]() và
và ![]() .
.
Cho hàm số ![]() có đạo hàm cấp hai trên khoảng
có đạo hàm cấp hai trên khoảng ![]() . Nếu
. Nếu ![]() thỏa mãn
thỏa mãn ![]() và
và ![]() thì
thì ![]() là điểm cực đại của hàm số
là điểm cực đại của hàm số ![]() Mệnh đề 4 đúng.
Mệnh đề 4 đúng.
Đồ thị hàm số ![]() có tiệm cận đứng
có tiệm cận đứng ![]() và tiệm cận ngang
và tiệm cận ngang ![]() Mệnh đề 5 đúng.
Mệnh đề 5 đúng.
Do đó ta chọn đáp án như sau
þ Nếu 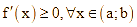 thì hàm số
thì hàm số ![]() đồng biến trên khoảng
đồng biến trên khoảng ![]() .
.
þ Hàm số ![]() luôn đồng biến trên
luôn đồng biến trên ![]()
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 15)
Cho hàm số ![]() xác định trên
xác định trên ![]() .
.
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
![]()
![]()
![]()
![]()
Giá trị lớn nhất của ![]() là _______.
là _______.
Cho ![]() , số nghiệm của phương trình
, số nghiệm của phương trình ![]() là: _______.
là: _______.
Số điểm biểu diễn nghiệm của bất phương trình ![]() trên đường tròn lượng giác là _______.
trên đường tròn lượng giác là _______.
Gọi ![]() là điểm biểu diễn số phức
là điểm biểu diễn số phức ![]() thỏa mãn
thỏa mãn ![]() .
.
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
|
|
ĐÚNG |
SAI |
|
Điểm |
¡ |
¡ |
|
|
¡ |
¡ |
Điền đáp án chính xác vào chỗ trống.
Theo hình 1, 16 giờ sau khi dùng dạng viên nén giải phóng kéo dài của thuốc theo toa, sự chênh lệch về nồng độ trung bình giữa thành phần A và thành phần B trong huyết tương gần nhất với (1)_________ ng/ml.
Nhận định sau đây đúng hay sai?
Nồng độ trong huyết tương trung bình của thành phần B được sử dụng dưới dạng viên nang phóng thích tức thời luôn thấp hơn nồng độ trong huyết tương trung bình của thành phần A trong khoảng 24 giờ sau khi dùng thuốc.
Trong không gian ![]() , cho điểm
, cho điểm ![]() . Gọi
. Gọi ![]() lần lượt là hình chiếu vuông góc của
lần lượt là hình chiếu vuông góc của ![]() trên trục
trên trục ![]() và trên mặt phẳng
và trên mặt phẳng ![]() .
.
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
|
|
ĐÚNG |
SAI |
|
Độ dài đoạn thẳng |
¡ |
¡ |
|
Phương trình mặt phẳng trung trực của đoạn |
¡ |
¡ |
Người ta muốn trang trí Tết bằng cách xếp xen kẽ 3 cây quất và 2 cây đào sao cho không có cây nào cùng loại xếp cạnh nhau.
Số cách xếp là _______.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.