Toptailieu biên soạn và giới thiệu Phương pháp giải bài tập Những hằng đẳng thức đáng nhớ (MỚI NHẤT 2024) gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 8 từ đó học tốt môn Toán. Mời các bạn đón xem:
Phương pháp giải bài tập Những hằng đẳng thức đáng nhớ (MỚI NHẤT 2024)
A. Bình phương của một tổng, bình phương của một hiệu và hiệu hai bình phương
I. Lý thuyết
1. Bình phương của một tổng:
2. Bình phương của một hiệu:
3. Hiệu hai bình phương
= (A – B)(A + B)
II. Các dạng bài
1. Dạng 1: Thực hiện phép tính
a. Phương pháp giải:
Sử dụng trực tiếp các hằng đẳng thức đã học để khai triển các biểu thức
b, Ví dụ minh họa:
VD1: Thực hiện phép tính:
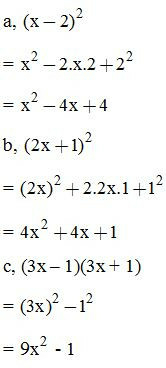
VD2: Viết các biểu thức sau dưới dạng bình phương một tổng hoặc bình phương một hiệu:
a,
b,
Giải:
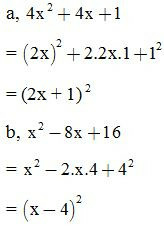
2. Dạng 2: Chứng minh các đẳng thức
a. Phương pháp giải:
Áp dụng linh hoạt các hằng đẳng thức, lựa chọn vế có thể dễ dàng áp dụng các hằng đẳng thức.
b. Ví dụ minh họa:
Chứng minh các đẳng thức sau:
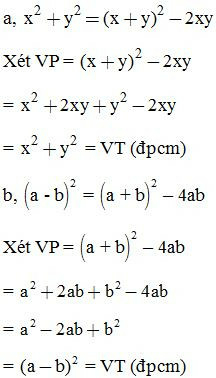
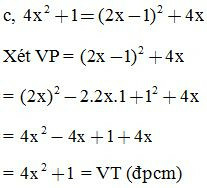
3. Dạng 3: Tính nhanh
a. Phương pháp giải:
Áp dụng linh hoạt các hằng đẳng thức cho các số tự nhiên
b. Ví dụ minh họa:
Tính nhanh:
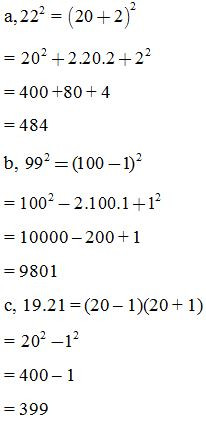
4. Dạng 4: Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
a. Phương pháp giải:
Sử dụng các hằng đẳng thức và cần chú ý:
và
b. Ví dụ minh họa:
a, Chứng minh luôn dương với mọi x
Giải:
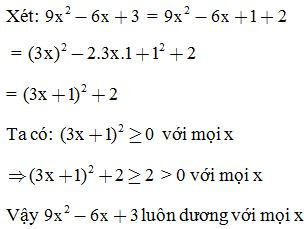
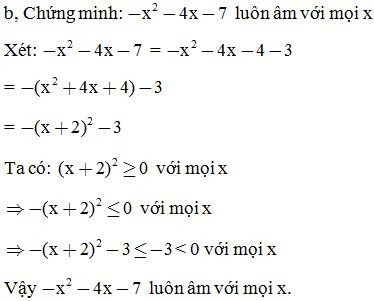
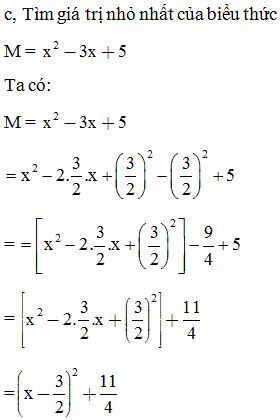
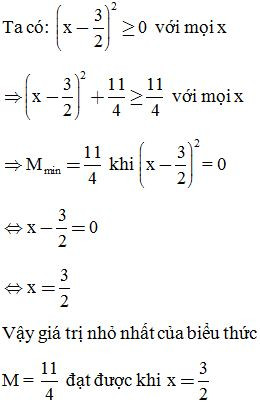
B. Lập phương của một tổng hoặc một hiệu
I. Lý thuyết
1. Lập phương của một tổng:
2. Lập phương của một hiệu:
II. Các dạng bài
1. Dạng 1: Sử dụng hằng đẳng thức để khai triển và rút gọn biểu thức và tính giá trị biểu thức:
a. Phương pháp giải:
Sử dụng hằng đẳng thức đã học để khai triển và rút gọn biểu thức.
b. Ví dụ minh họa:
VD1: Thực hiện phép tính:
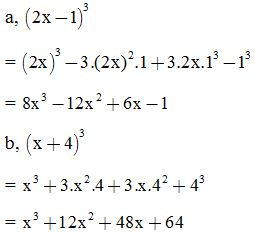
VD2: Rút gọn biểu thức:
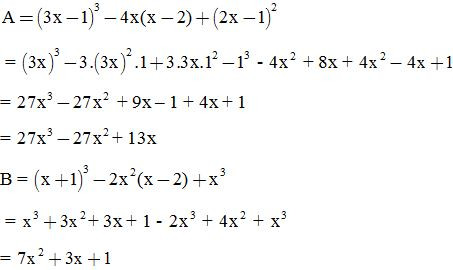
VD3: Viết các biểu thức sau dưới dạng lập phương một tổng hoặc lập phương một hiệu:
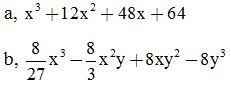
Giải:
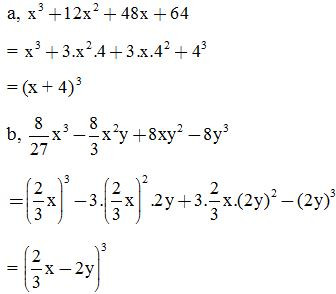
VD4: Tính giá trị các biểu thức sau:
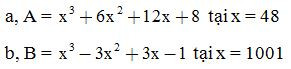
Giải:
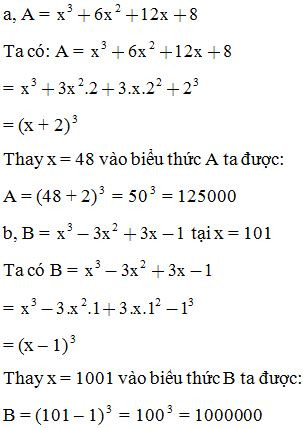
2. Dạng 2: Sử dụng hằng đẳng thức để tính nhanh:
a. Phương pháp giải:
Sử dụng linh hoạt các hằng đẳng thức để tính nhanh
b. Ví dụ minh họa:
Tính nhanh:
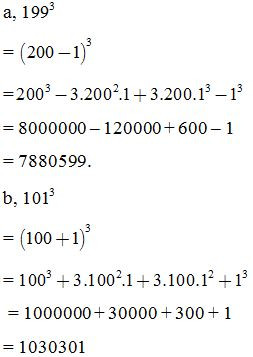
C. Tổng hoặc hiệu hai lập phương
I. Lý thuyết:
1. Tổng hai lập phương:
2. Hiệu hai lập phương:
II. Các dạng bài:
1. Dạng 1: Sử dụng hằng đẳng thức để rút gọn và khai triển biểu thức:
a. Phương pháp giải:
Sử dụng các hằng đẳng thức đã học để khai triển hoặc rút gọn biểu thức.
b. Ví dụ minh họa:
VD1: Thực hiện phép tính:
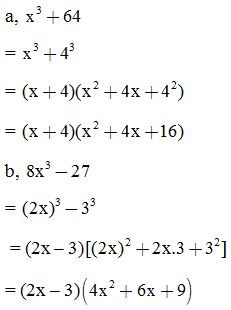
VD2: Rút gọn biểu thức:
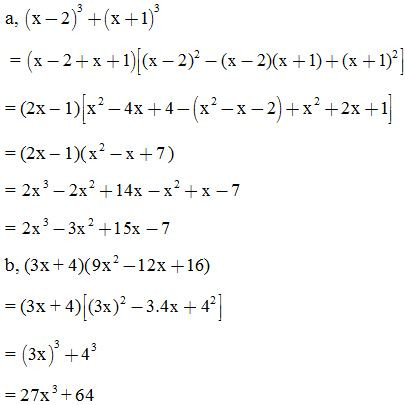
2. Dạng 2: Sử dụng hằng đẳng thức để tính nhanh
a, Phương pháp giải:
Sử dụng các hằng đẳng thức đã học để phân tích và tính
Chú ý thêm:
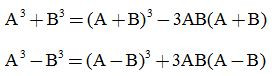
b, Ví dụ minh họa:
Tính nhanh:
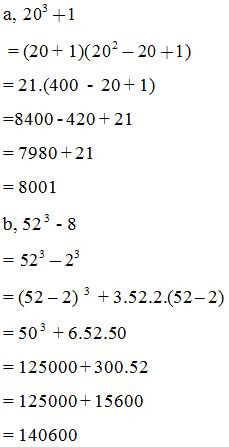
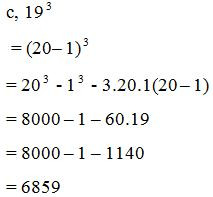
III. Bài tập tự luyện
Bài 1: Thực hiện phép tính:
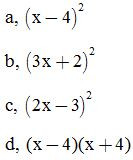
ĐS:
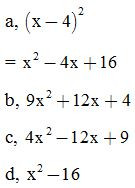
Bài 2: Thực hiện phép tính:
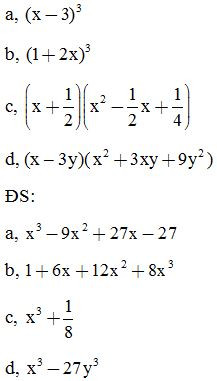
Bài 3: Viết các biểu thức dưới dạng bình phương của một tổng hoặc hiệu:
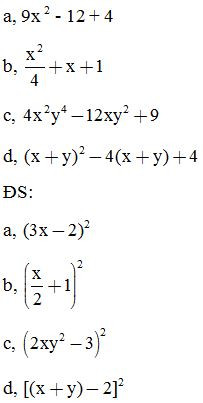
Bài 4: Chứng minh các đẳng thức sau:
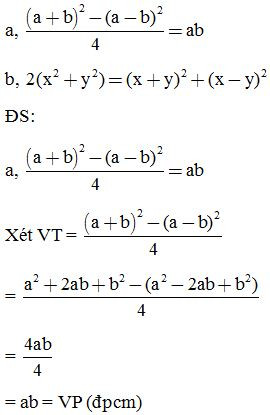
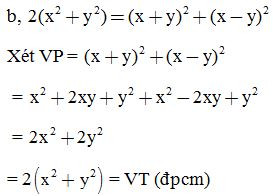
Bài 5: Rút gọn biểu thức:
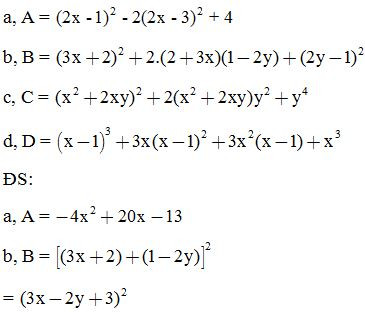
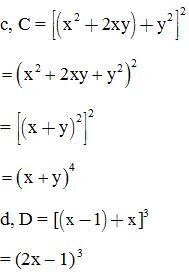
Bài 6: Rút gọn biểu thức:
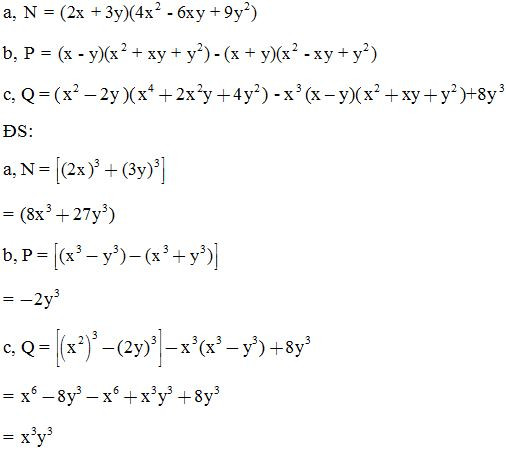
Bài 7: Tính giá trị của các biểu thức sau:
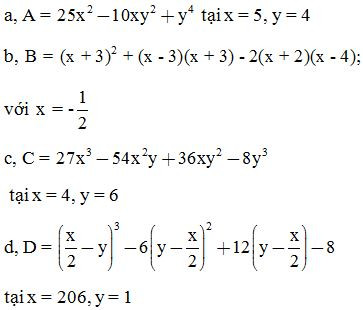
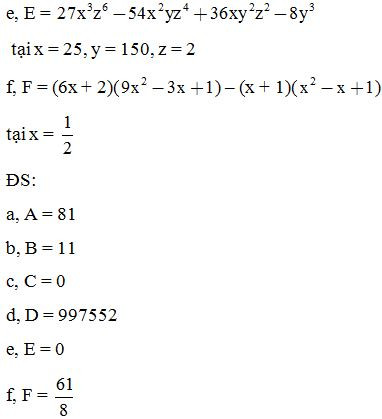
Bài 8: Tính nhanh:
a, 292
b, 62.58
c, 1022
d, 1013
e, 913 + 3.912 .9 + 3.91.92 + 93
f, 183 - 3.182 .8 + 3.18.82 - 2
g, 183+23
h, 233 - 27
ĐS:
a, 292
= (30 – 1)2
= 841
b, 62.58
= (60 + 2)(60 – 2)
= 602 - 22
= 3596
c, 1022
= (100 + 2)2
= 10404
d, 1013
= (100 + 1)3
= 1030301
e, 913 + 3.912 .9 + 3.91.92 + 93
= (91 + 9)3
= 1003
= 1000000
f, 183 - 3.182 .8 + 3.18.82 - 29
= (18 – 8)3
= 103
= 1000
g, 183 + 23
= (18 + 2)3 – 3.18.2(18 + 2)
= 203 - 6.18.20
= 5840
h, 233 - 27
= 233 - 33
= (23 – 3)3 + 3.23.3.(23 – 3)
= 203 + 9.23.20
= 12140
Bài 9: Tính giá trị biểu thức:
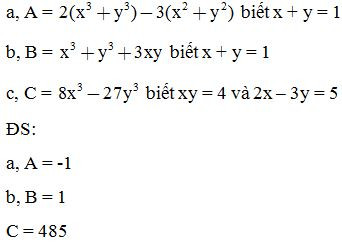
Bài 10: Chứng minh các biểu thức sau không phụ thuộc vào giá trị của biến x:
a, A =3(x – 1)2 - (x + 1)2 + 2(x – 3)(x + 3) – (2x + 3)2 - (5 – 20x)
b, B = -x(x + 2)2 + (2x + 1)2 + (x + 3)(x2 - 3x + 9) – 1
ĐS:
a, A = - 30
b, B = 27
Bài 11: Tính giá trị nhỏ nhất của biểu thức:
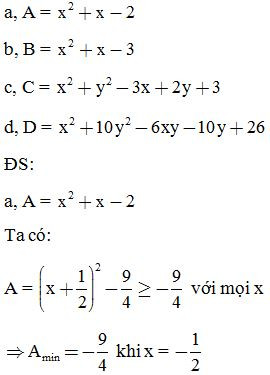
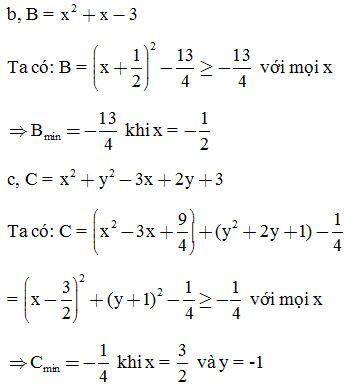
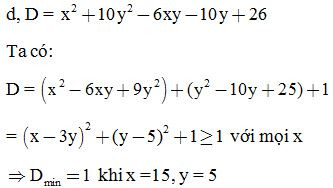
Bài 12: Tìm giá trị lớn nhất của biểu thức:
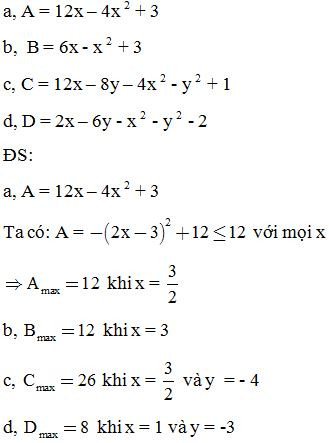
Bài 13: Chứng minh rằng với mọi a, b, c ta luôn có:
(a + b + c)3 = a3 + b3 + c3 + 3(a + b)(b + c)(c + a)
ĐS: Hướng dẫn:
Đặt a + b = A, B = c
Ta có: VT = (a + b + c)3
= (A + B)3 = A3 + B + 3A2B + 3AB2
Thay vào ta được:
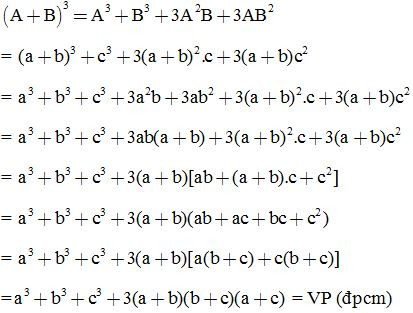
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.