Toptailieu biên soạn và giới thiệu Phương pháp giải Cách chia đa thức một biến đã sắp xếp (50 bài tập minh họa) gồm các dạng bài tập có phương pháp giải chi tiết và các bài tập điển hình từ cơ bản đến nâng cao giúp học sinh biết cách làm các dạng toán.
Phương pháp giải Cách chia đa thức một biến đã sắp xếp (50 bài tập minh họa)
A. Lý thuyết:
- Muốn chia đa thức một biến A cho đa thức một biến B0, trước hết ta phải sắp xếp các đa thức này theo lũy thừa giảm dần của cùng một biến và thực hiện phép chia như phép chia các số tự nhiên
- Với A và B là hai đa thức tùy ý cùng một biến số (B0), khi đó tồn tại duy nhất một cặp đa thức Q và R sao cho A = B.Q + R.
Trong đó R = 0 hoặc bậc của R nhỏ hơn bậc của B.
Nếu R = 0 thì phép chia A cho B là phép chia hết.
R0 thì phép chia A cho B là phép chia có dư.
Q được gọi là đa thức thương, R được gọi là dư trong phép chia A cho B.
B. Các dạng bài:
Dạng 1: Sử dụng hằng đẳng thức để thực hiện phép chia đa thức
1. Phương pháp giải: Có thể dùng các hằng đẳng thức đấng nhớ sau để rút gọn phép chia đa thức:
2. Ví dụ minh hoạ: Áp dụng hẳng đẳng thức đáng nhớ để thực hiện các phép chia sau:
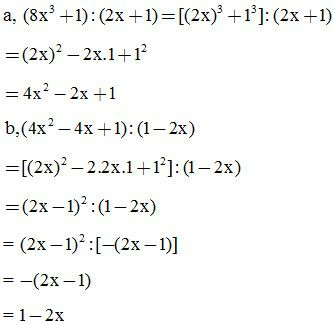
Dạng 2: Tìm thương và số dư trong phép chia đa thức
1. Phương pháp giải: Từ điều kiện đề bài đã cho, đặt phép chia A cho B rồi viết A dưới dạng A = B.Q + R
2. Ví dụ minh họa:
a, Cho hai đa thức A = và B = . Tìm dư R trong phép chia A cho B và viết A dưới dạng A = B.Q + R
b, Cho đa thức A = và B = . Tìm dư R trong phép chia A cho B và viết A dưới dạng A = B.Q + R
Hướng dẫn giải:
a, Ta thực hiện phép chia sau:
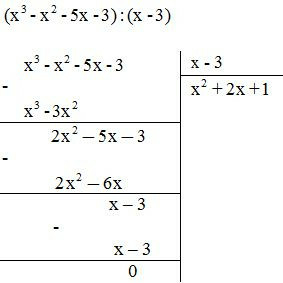
KL:
- Vậy số dư trong phép chia là 0
A = (x - 3).() + 0
b, Ta thực hiện phép chia sau:
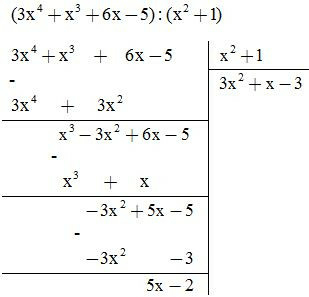
KL:
- Vậy số dư trong phép chia là 5x – 2
A = ().() + (5x – 2)
Dạng 3: Tìm điều kiện để thực hiện phép chia đa thức
1. Phương pháp giải:
* Thực hiện phép chia A : B để tìm biểu thức dư R theo m
Để A chia hết cho B thì R = 0m
* Tìm số nguyên n để A chia hết cho B (với A , B là các biểu thức theo n)
- Thực hiện A : B tìm số dư là số nguyên k, thương là biểu thức Q
- Viết A = Q.B + k
- Để A chia hết cho Bk chia hết cho BB là Ư(k)n
2. Ví dụ minh họa:
VD1: Tìm k để chia hết cho g(x) = x – 2
Giải: Ta thực hiện phép chia sau:

Để f(x) chia hết cho g(x) thì k + 30 = 0k = - 30.
KL: Vậy với k = -30 thì f(x) chia hết cho g(x)
VD2: Tìm số nguyên x để đa thức A = 8x2 - 4x +1 chia hết cho đa thức B = 2x + 1
Giải: Ta thực hiện phép chia sau:
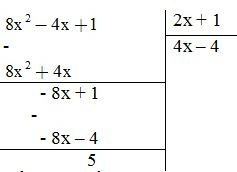
Để A chia hết cho B thì 5 (2x + 1) (2x + 1)Ư(5)
|
2x + 1 |
5 |
-5 |
1 |
-1 |
|
x = |
2 (TM) |
-3 (TM) |
0 (TM) |
-1 (TM) |
KL: Vậy x = {-3, -1, 0, 2}
3. Bài tập tự luyện
Bài 1: Thực hiện phép chia sau:
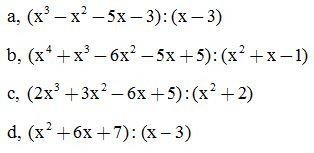
Đs:
a, Đây là phép chia hết với đa thức thương bằng
b, Đa thức thương bằng
c, Đây là phép chia dư với đa thức thương bằng 2x + 3 và dư ( - 10x -1)
d, Đây là phép chia dư với đa thức thương bằng x + 9 và dư 34
Bài 2: Sắp xếp các đa thức theo lũy thừa giảm dần của biến rồi tính:
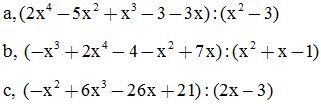
Đs:
a, Đây là phép chia hết với đa thức thương bằng
b, Đây là phép chia hết với đa thức thương bằng
c, Đây là phép chia hết với đa thức thương bằng
Bài 3: Sử dụng hẳng đẳng thức để thực hiện các phép chia sau:
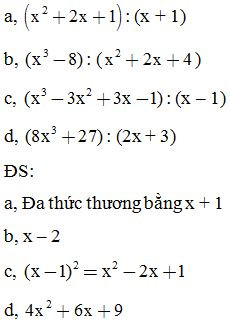
Bài 4: Phân tích đa thức thành nhân tử rồi thực hiện phép chia:
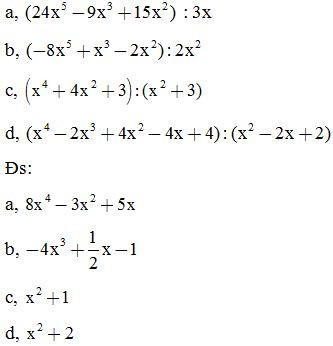
Bài 5: Tìm thương Q và dư R sao cho A = B.Q + R, biết:
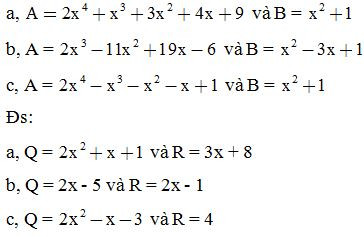
Bài 6: Tìm k để:
a, f(x) = x4 – 10x3 + 21x2 + 8x + k chia hết cho g(x) = x + 2
b, f(x) = x4 – 19x3 + 25x2 - 6x + k chia hết cho g(x) = x – 3
c, f(x) = x4 – 8x3 + 24x2 + 7x + k chia hết cho g(x) = x + 4
d, f(x) = 3x4 – 7x3 + 11x2 + x + k chia hết cho g(x) = x – 4
ĐS:
a, k = - 164
b, k = 225
c, k = -1124
d, k = 500
Bài 7: Tìm a và b để đa thức A chia hết cho đa thức B, biết:
a) A = x4 – 3x3 + 3x2 + ax + b và B = x2 - 3x + 4
b) A = x4 – 9x3 + 21x2 + ax + b và B = x2 - x - 2
ĐS:
a, a = 3, b = -4
b, a = 1, b = -30
Bài 8: Tìm giá trị nguyên của x để đa thức A chia hết cho đa thức B, biết:
a, A = 3x3 + 8x2 - 15x + 6 và B = 3x – 1
b, A = x3 + 4x2 + ax - 7 và B = x + 4
ĐS:
a, x = 0, x = 1
b, x = {-23, -5, -3, 15}
Bài 9: Tìm đa thức M, biết:
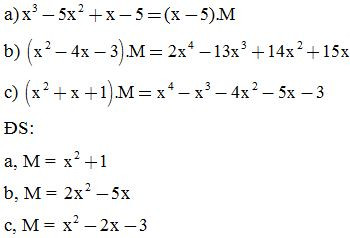
Bài 10: Tìm x biết:
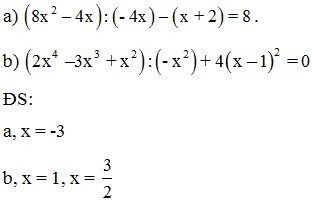
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.