Toptailieu biên soạn và giới thiệu Phương pháp giải Đa giác, Đa giác lồi, Đa giác đều (50 bài tập minh họa) gồm các dạng bài tập có phương pháp giải chi tiết và các bài tập điển hình từ cơ bản đến nâng cao giúp học sinh biết cách làm các dạng toán.

Phương pháp giải Đa giác, Đa giác lồi, Đa giác đều (50 bài tập minh họa)

I. Lý thuyết

1. Đa giác

- Đa giác là hình gồm n đoạn thẳng ; ; …; trong đó không có bất kỳ hai đoạn thẳng nào có một điểm chung cùng nằm trên một đường thẳng.

Hình a là đa giác ABCDEF là hình gồm 6 cạnh hay còn gọi là lục giác

Hình b là đa giác GHIJK là hình gồm 5 cạnh hay còn gọi là ngũ giác

- Đa giác có n đỉnh gọi là hình n – giác hay hình n cạnh.

- Đường chéo của đa giác là đoạn thẳng nối hai đỉnh không kề nhau của đa giác đó.

- Số đường chéo của đa giác được tính theo công thức:

$\frac{n\left(n-3\right)}{2}$ với n là số đỉnh của đa giác và n > 3

- Tổng số đo các góc trong một hình n – giác là:

$\left(n-2\right).180°$ với n là số đỉnh, n > 2

2. Đa giác lồi

Đa giác lồi là đa giác luôn nằm trên nửa mặt phẳng với bờ là đường thẳng chứa một cạnh bất kỳ của đa giác.

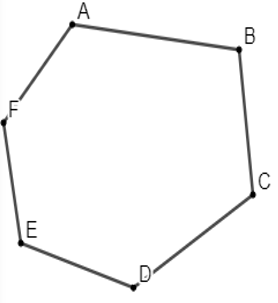
Đa giác ABCDEF là một đa giác lồi do đa giác luôn nằm trên nửa mặt phẳng có bờ là một đường thẳng chứa một cạnh bất kỳ của đa giác.

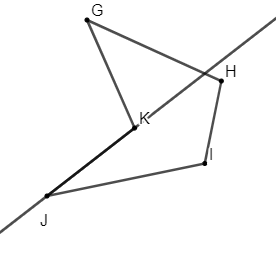
Đa giác GHIJK không phải đa giác lồi vì đa giác không nằm hoàn toàn trên nửa mặt phẳng có bờ là đường thẳng chứa cạnh JK.

Chú ý: Từ nay, khi nói đến đa giác mà không chú thích gì thêm, ta hiểu đó là đa giác lồi.

3. Đa giác đều

- Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.

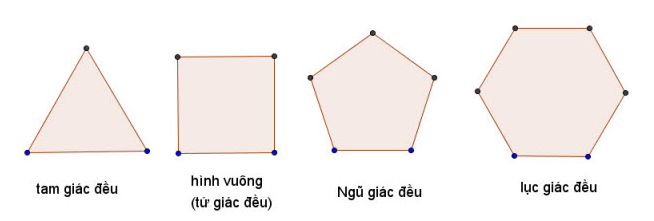
Số đo mỗi góc trong đa giác đều n đỉnh được tính theo công thức:

$\frac{\left(n-2\right).180°}{n}$ với n là số đỉnh, n > 2.

II. Dạng bài tập

Dạng 1: Nhận dạng đa giác, đa giác lồi, đa giác đều

Phương pháp giải: Sử dụng định nghĩa về đa giác, đa giác đều, đa giác lồi.

Ví dụ 1: Cho ngũ giác ABCDE. Kẻ các đường chéo AC và AD. Kể tên các đa giác có trong hình vẽ

Lời giải:

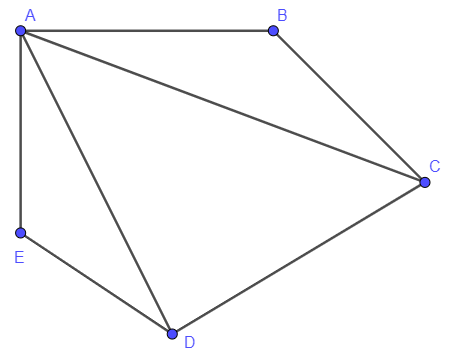
Các đa giác có trong hình vẽ là:

Tam giác ABC; ACD; ADE

Tứ giác ABCD; ACDE

Ngũ giác là ABCDE

Ví dụ 2: Cho các hình vẽ sau

Giải thích tại sao hai đa giác trên không phải đa giác lồi

Lời giải:

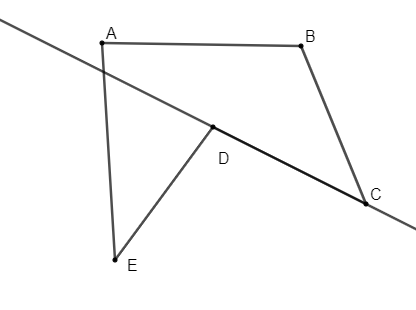
 Đa giác ABCDE không phải đa giác lồi vì đa giác không nằm hoàn toàn trong nửa mặt phẳng có bờ là đường thẳng chứa cạnh DC.

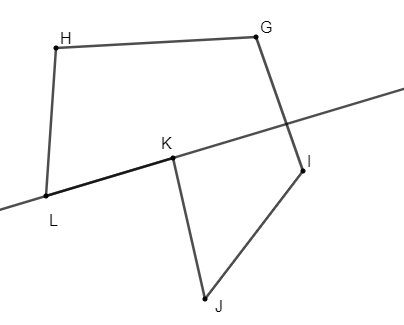
Đa giác GIJKLH không phải đa giác lồi vì đa giác không nằm hoàn toàn trong nửa mặt phẳng có bờ là đường thẳng chứa cạnh LK.

Ví dụ 3: Cho hình thoi ABCD có $\widehat{A}=60°$ . Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh MBNPDQ là lục giác đều.

Lời giải:

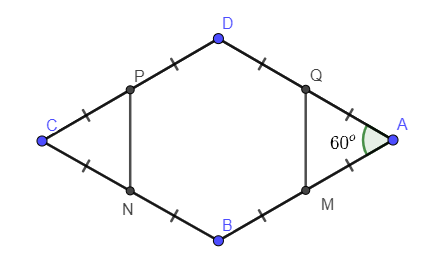
Vì ABCD là hình thoi nên AB = BC = CD = DA

Lại có M là trung điểm của AB$\Rightarrow BM=AM=\frac{1}{2}AB$

N là trung điểm của BC$\Rightarrow CN=NB=\frac{1}{2}BC$

P là trung điểm của CD$\Rightarrow PC=PD=\frac{1}{2}DC$

Q là trung điểm của AD$\Rightarrow AQ=QD=\frac{1}{2}AD$

Do đó: AM = BM = CN = NB = CP = PD = AQ = QD  (1)

Xét tam giác AQM có:

$\left\{\begin{array}{l}AQ=AM\\ \widehat{QAM}=60°\end{array}\right.$

$\Rightarrow \Delta AQM$là tam giác đều

$\Rightarrow AM=MQ$ (2)

Do ABCD là hình thoi

$\Rightarrow \widehat{QAM}=\widehat{NCP}=60°$(tính chất)

Xét tam giác CPN có

$\left\{\begin{array}{l}CP=CN\\ \widehat{NCP}=60°\end{array}\right.$

$\Rightarrow \Delta CPN$ là tam giác đều

$\Rightarrow CN=PN$ (3)

Từ (1); (2); (3)  BM = BN = NP = PD = DQ = QM (*)

Xét hình thoi ABCD có

$\widehat{A}=\widehat{C}=60°$$\Rightarrow \widehat{B}=\widehat{D}=120°$(4)

Ta có: $\widehat{AMQ}$ và $\widehat{BMQ}$  là hai góc kề bù

 $\Rightarrow \widehat{BMQ}+\widehat{AMQ}=180°$

Mà $\widehat{AMQ}=60°$ do tam giác AMQ đều

$\Rightarrow \widehat{BMQ}+60°=180°$

$\Rightarrow \widehat{BMQ}=120°$(5)

Chứng minh tương tự ta được các góc $\widehat{DQM}=\widehat{BNP}=\widehat{DPN}=120°$ (6)

Từ (4); (5); (6)

$\Rightarrow \widehat{B}=\widehat{D}=\widehat{BMQ}=\widehat{DQM}=\widehat{BNP}=\widehat{DPN}=120°$(**)

Xét lục giác MBNPDQ có:

BM = BN = NP = PD = DQ = QM (theo (*))

(theo (**))

Vậy lục giác MBNPDQ là lục gác đều.

Dạng 2: Tính góc và số đường chéo của đa giác

Phương pháp giải: Áp dụng các công thức về tính góc và đường chéo của đa giác

- Số đường chéo của đa giác được tính theo công thức:

$\frac{n\left(n-3\right)}{2}$ với n là số đỉnh của đa giác và n > 3

- Tổng số đo các góc trong một hình n – giác là:

$\left(n-2\right).180°$ với n là số đỉnh, n > 2

Số đo mỗi góc trong đa giác đều n đỉnh được tính theo công thức:

$\frac{\left(n-2\right).180°}{n}$ với n là số đỉnh

Ví dụ 1: Tính số đường chéo của một hình lục giác.

Lời giải:

Vì lục giác là hình có 6 đỉnh nên áp dụng công thức tính số đường chéo của đa giác ta có:

Số đường chéo của hình lục giác là:

$\frac{n\left(n-3\right)}{2}=\frac{6\left(6-3\right)}{2}=9$ (đường chéo)

Ví dụ 2: Một đa giác đều có n cạnh. Mỗi góc của nó bằng $156°$ . Tính số cạnh của đa giác đó.

Lời giải:

Áp dụng công thức tính số đo mỗi giác trong đa giác đều ta có:

$\frac{\left(n-2\right)180°}{n}=156°$

$\iff \left(n-2\right)180°=n156°$

$\iff n.180°-360°=n.156°$

$\iff n.180°-n.156°=360°$

$\iff n\left(180°-156°\right)=360°$

$\iff n.24°=360°$

$\iff n=360°:24°$

$\iff n=15$

Vậy đa giác đều này có 15 cạnh.

III. Bài tập vận dụng