Toptailieu biên soạn và giới thiệu Phương pháp giải Diện tích hình chữ nhật (50 bài tập minh họa) gồm các dạng bài tập có phương pháp giải chi tiết và các bài tập điển hình từ cơ bản đến nâng cao giúp học sinh biết cách làm các dạng toán.

Phương pháp giải Diện tích hình chữ nhật (50 bài tập minh họa)

I. Lý thuyết

1. Khái niệm diện tích đa giác

- Số đo phần mặt phẳng bị giới hạn bởi đa giác gọi là diện tích đa gác.

- Mỗi đa giác chỉ có một số đo diện tích nhất định. Số đo đó là một số dương

- Một số tính chất của diện tích đa giác:

+ Hai tam giác bằng nhau thì có diện tích bằng nhau.

+ Nếu một đa giác được chia thành những đa giác không có điểm trong chung thì diện tích của đa giác bằng tổng diện tích các đa giác đã chia.

+ Nếu chọn một hình vuông có độ dài cạnh là 1cm; 1dm; 1m làm đơn vị đo diện tích thì đơn vị diện tích của hình vuông đó tương ứng là 1 $c{m}^2$ ; 1 $d{m}^2$ ; 1 $m^2$

2. Công thức tính diện tích hình chữ nhật

Diện tích hình chữ nhật bằng tích hai kích thước của nó (tích chiều dài và chiều rộng)

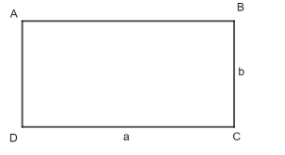
Cho hình chữ nhật ABCD có DC = a; BC = b

Diện tích hình chữ nhật: S = a.b (đơn vị diện tích)

3. Diện tích hình vuông

Diện tích hình vuông bằng bình phương độ dài cạnh của nó.

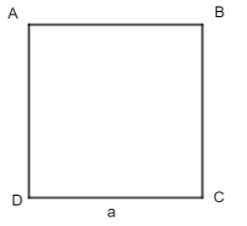
Hình vuông ABCD có độ dài cạnh bằng a

Diện tích hình vuông: S = $a^2$(đơn vị diện tích)

4. Diện tích tam giác vuông

Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông

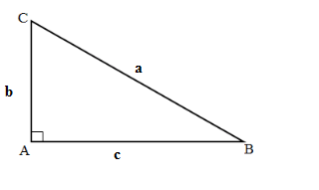
Cho tam giác ABC vuông tại A  có AB = c; AC = b

Diện tích tam giác vuông ABC: S = $\frac{1}{2}bc$  (đơn vị diện tích)

II. Dạng bài tập

Dạng 1: Tính diện tích đa giác

Phương pháp giải: Sử dụng các khái niệm diện tích của đa giác và cách chia nhỏ một đa giác.

Ví dụ: Cho hình bình hành ABCD, M là trung điểm của cạnh BC. Tia AM cắt tia DC tại điểm E. Chứng minh:$S_{ABCD}=S_{AED}$

Lời giải:

Vì M là trung điểm của BC nên BM = MC

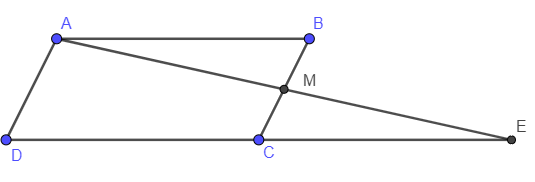
Vì AB // CD nên AB // CE$\Rightarrow \widehat{ABM}=\widehat{ECM}$ (hai góc so le trong)

Xét hai tam giác ABM và tam giác ECM có:

BM = CM (chứng minh trên)

$\widehat{ABM}=\widehat{ECM}$(chứng minh trên)

$\widehat{AMB}=\widehat{EMC}$(hai góc đối đỉnh)

Do đó $\Delta ABM=\Delta ECM$ (g – c – g)

$\Rightarrow S_{ABM}=S_{ECM}$  (1)

Ta có:

 $S_{ABCD}=S_{ABM}+S_{AMCD}$ (2)

 $S_{AED}=S_{ECM}+S_{AMCD}$ (3)

Từ (1), (2) và (3)  (điều phải chứng minh)

Dạng 2: Bài toán liên quan đến diện tích hình chữ nhật

Phương pháp giải: Sử dụng công thức tính diện tích hình chữ nhật

S = a.b (đơn vị diện tích)

với a, b là chiều dài và chiều rộng

Công thức tính chu vi hình chữ nhật

C = (a + b). 2 (đơn vị độ dài)

Ví dụ 1: Một hình chữ nhật có chu vi là 50cm và diện tích là 150 . Tính chiều dài, chiều rộng của hình chữ nhật.

Lời giải:

Nửa chu vi hình chữ nhật là:

Gọi chiều dài của hình chữ nhật là x ( 0 < x < 25)

Khi đó chiều rộng của hình chữ nhật là 25 – x

Chiều dài lớn hơn chiều rộng x > 25 – x

$\iff$x > 12, 5

Vậy điều kiện của x là 12,5 < x < 25

Diện tích hình chữ nhật là x(25 – x)$c{m}^2$

Mà diện tích hình chữ nhật là 150 $c{m}^2$ nên ta có:

$x\left(25-x\right)=150$

$\iff 25x-x^2=150$

$\iff x^2-25x+150=0$

$\iff x^2-15x-10x+150=0$

$\iff x\left(x-15\right)-10\left(x-15\right)=0$

$\iff \left(x-15\right)\left(x-10\right)=0$

$\Rightarrow \left[\begin{array}{l}x-15=0\\ x-10=0\end{array}\right.$

$\iff \left[\begin{array}{l}x=15\text{ (tm)}\\ x=10\text{ (ktm)}\end{array}\right.$

Với chiều dài hình chữ nhật là 15cm chiều rộng hình chữ nhật là : 25 – 15 = 10cm

Vậy chiều dài hình chữ nhật là 15cm; chiều rộng hình chữ nhật là 10cm

Ví dụ 2: Hình chữ nhật có diện tích là 6000 $c{m}^2$ . Nếu chiều dài tăng thêm 20cm và chiều rộng giảm 5cm thì diện tích tăng 600 $c{m}^2$ .  Tính chu vi hình chữ nhật ban đầu.

Lời giải:

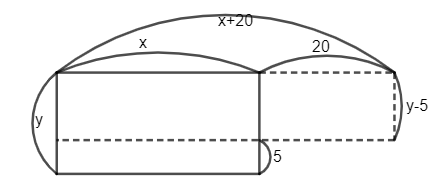
Gọi chiều dài ban đầu của hình chữ nhật là x, chiều rộng ban đầu của hình chữ nhật là y (0 < y < x)

Diện tích ban đầu của hình chữ nhật là xy $\left(c{m}^2\right)$

Chiều dài hình chữ nhật sau khi tăng thêm 20cm là x + 20 (cm)

Chiều rộng hình chữ nhật sau khi giảm 5cm là y – 5 (cm)

Diện tích hình chữ nhật mới là: (x + 20)(y – 5) = xy + 20y – 5x – 100$\left(c{m}^2\right)$

Vì diện tích mới tăng thêm 600 $c{m}^2$ ta có:

xy + 20y – 5x – 100 – xy = 600

$\iff$-5x + 20y – 100 = 600

$\iff$20y – 5x = 600 + 100

$\iff$20y – 5x = 700

$\iff$4y – x = 140

$\iff$x = 4y – 140

Mà xy = 6000 $c{m}^2$  nên ta có:

(4y – 140)y = 6000

$\iff 4y^2-140y=6000$

$\iff y^2-35y-1500=0$

$\iff y^2-60y+25y-1500=0$

$\iff y\left(y-60\right)+25\left(y-60\right)=0$

$\iff \left(y+25\right)\left(y-60\right)=0$

$\iff \left[\begin{array}{l}y+25=0\\ y-60=0\end{array}\right.$

$\iff \left[\begin{array}{l}y=-25\text{ (ktm)}\\ y=60\text{ (tm)}\end{array}\right.$

Với y = 60 cm $\Rightarrow x=6000:60=100$ cm

Chu vi hình chữ nhật ban đầu là:

C = (a + b). 2 = (100 + 60).2 = 320cm

Dạng 3: Bài toán liên quan đến diện tích hình vuông

Phương pháp giải: Sử dụng công thức tính diện tích hình vuông

Hình vuông có cạnh bằng a: diện tích hình vuông: S = $a^2$ (đơn vị diện tích)

Chu vi hình vuông có cạnh bằng a: c = 4.a (đơn vị độ dài)

Ví dụ 1: Một hình vuông có cạnh bằng a. Khi độ dài mỗi cạnh tăng 5% thì diện tích hình vuông tăng bao nhiêu %?

Lời giải:

Diện tích hình vuông có cạnh bằng a là: $a^2$ (đơn vị diện tích)

Khi độ dài mỗi cạnh 5% thì độ dài cạnh hình vuông mới là: a + a.5% = a + 0,05a = 1,05a (đơn vị độ dài)

Diện tích hình vuông mới có cạnh 1,05a là:${\left(\mathrm{1,05}a\right)}^2=\mathrm{1,1025}{a}^2$ (đơn vị diện tích)

Tỉ số % diện tích hình vuông mới so với hình vuông ban đầu là:

1,1025 $a^2$ : $a^2$ .100% = 110,25%

% diện tích tăng thêm là:

110,25% - 100% = 10,25%

Vậy diện tích tăng thêm là 10,25%.

Ví dụ 2: Một hình chữ nhật có diện tích là 192 $c{m}^2$ . Biết tỉ lệ của chiều rộng và chiều dài là 1:3.

Tính diện tích hình vuông có cùng chu vi với diện tích hình chữ nhật trên.

Lời giải:

Gọi chiều rộng hình chữ nhật là x (cm) thì chiều dài của hình chữ nhật là 3x (cm).

Diện tích hình chữ nhật là : 3x.x = 192$c{m}^2$

$\iff 3x^2=192$

$\iff x^2=192:3$

$\iff x^2=64$

$\Rightarrow x=8$(cm)

Chiều rộng của hình chữ nhật là 8cm

Chiều dài của hình chữ nhật là 3.8 = 24cm

Chu vi hình chữ nhật là:

(8 + 24). 2 = 64cm

Cạnh hình vuông có cùng chu vi với hình chữ nhật là

64 : 4 = 16cm

Diện tích hình vuông có cùng chu vi với hình chữ nhật là:

$S=16.16=256c{m}^2$

Vậy diện tích hình vuông là $256c{m}^2$

Dạng 4: Các bài toán có liên quan đến diện tích tam giác vuông

Phương pháp giải: Sử dụng định lý Py – ta – go và công thức thức tính diện tích tam giác vuông.

Tam giác ABC vuông tại A .

Diện tích tam giác ABC: S =$\frac{1}{2}AB.AC$

$A{B}^2+A{C}^2=B{C}^2$

Ví dụ 1: Cho tam giác ABC vuông tại A có AB = 3cm; BC = 5cm. Tính diện tích tam giác ABC.

Lời giải:

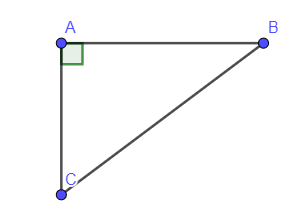
Xét tam giác ABC vuông tại A ta có:

$A{B}^2+A{C}^2=B{C}^2$(Định lý Py – ta – go)

$\iff 3^2+A{C}^2=5^2$

$\iff 9+A{C}^2=25$

$\iff A{C}^2=25-9$

$\iff A{C}^2=16$

$\Rightarrow AC=4cm$

$S=\frac{1}{2}AB.AC=\frac{1}{2}3.4=6c{m}^2$

Vậy diện tích tam giác ABC là $6c{m}^2$ .

Ví dụ 2: Tính diện tích tam giác vuông có cạnh huyền bằng 13 và tổng hai cạnh góc vuông là 17.

Lời giải:

Gọi cạnh góc vuông thứ nhất là x cm (0 < x < 17).

Vì tổng hai cạnh góc vuông là 17 nên cạnh góc vuông thứ hai là 17 – x cm

Giả sử x là cạnh góc vuông lớn trong hai cạnh góc vuông

 $\Rightarrow x>17-x$

$\iff 2x>17$

$\iff x>17:2$

$\iff x>\mathrm{8,5}$

Áp ụng định lý Py – ta – go cho tam giác vuông ta có:

$x^2+{\left(17-x\right)}^2={13}^2$

$\iff x^2+289-34x+x^2=169$

$\iff 2x^2-34x+289-169=0$

$\iff 2x^2-34x+120=0$

$\iff 2x^2-24x-10x+120=0$

$\iff 2x\left(x-12\right)-10\left(x-12\right)=0$

$\iff \left(x-12\right)\left(2x-10\right)=0$

$\iff \left[\begin{array}{l}x-12=0\\ 2x-10=0\end{array}\right.$

$\iff \left[\begin{array}{l}x=12\\ 2x=10\end{array}\right.$

$\iff \left[\begin{array}{l}x=12\text{ (tm)}\\ x=5\text{ (ktm)}\end{array}\right.$

Với x = 12 thì độ dài hai cạnh góc vuông lần lượt là 12cm và 5cm

Diện tích tam giác vuông cần tính là:

.$S=\frac{1}{2}\mathrm{.12.5}=30c{m}^2$

III. Bài tập vận dụng

Bài 1: Cho hình bình hành ABCD. Từ A và C kẻ AH và CK vuông góc với BD. Chứng minh:

a)$S_{ABCH}=S_{ADCK}$

b)$S_{ABCK}=S_{ADCH}$

Bài 2: Cho hình chữ nhật có độ dài đường chéo là 40cm và các cạnh tỉ lệ với 3 và 4. Tính chu vi và diện tích hình chữ nhật đó.

Bài 3: Một thửa ruộng hình chữ nhật. Nếu tăng chiều dài thêm 20m và chiều rộng giảm đi 5m thì diện tích tăng 600 $m^2$ . Nếu giảm chiều dài đi 10m và tăng chiều rộng lên 10m thì diện tích tăng 300 $m^2$ . Tính diện tích hình chữ nhật ban đầu.

Bài 4: Một hình chữ nhật ABCD có AD = 7cm, BD = 25cm. Gọi O là giao điểm 2 đường chéo. Gọi M, N, P, Q theo thứ tự là trung điểm của OA, OB, OC, OD. Tính diện tích tứ giác MNPQ.

Bài 5: Cho tam giác ABC vuông tại A. Dựng phía ngoài tam giác hình vuông ABFG, ACKI, BCDE. Chứng minh:

a)$S_{FBC}=S_{ABE}$

b)$S_{BCDE}=S_{ABFG}+S_{ACKI}$

Bài 6: Nếu tăng độ dài mỗi cạnh hình vuông lên 3 lần thì diện tích hình vuông tăng lên mấy lần?

Bài 7: Một hình thang cân có hai đường chéo vuông góc với nhau. Độ dài đường chéo là 6cm. Tính diện tích tứ giác có các đỉnh là trung điểm các cạnh của hình thang cân đó.

Bài 8: Cho hình bình hành ABCD. Các tia phân giác góc A và C cắt đường chéo BD tại E và F. Chứng minh:

a)$S_{ABCFE}=S_{ADCFE}$

b)$S_{ABCE}=S_{ADCF}$

Bài 9: Cho tam giác ABC vuông tại A. Có AB = 6; BC = 10. Tính diện tích tam giác ABC.

Bài 10: Trong các hình chữ nhật có cùng diện tích là 100 $c{m}^2$ hình nào có chu vi nhỏ nhất.