Toptailieu biên soạn và giới thiệu Phương pháp giải Công thức diện tích hình thang (50 bài tập minh họa) gồm các dạng bài tập có phương pháp giải chi tiết và các bài tập điển hình từ cơ bản đến nâng cao giúp học sinh biết cách làm các dạng toán.
Nội dung bài viết
Phương pháp giải Công thức diện tích hình thang (50 bài tập minh họa)
I. Lý thuyết
- Diện tích hình thang bằng nửa tích của tổng hai đáy với chiều cao
S=12(a+b).h trong đó: a, b là độ dài hai đáy, h là độ dài đường cao.
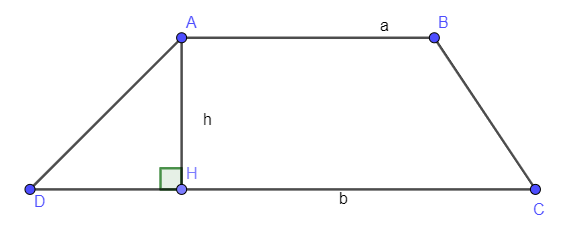
Cho hình thang ABCD có AB // CD, AB = a, DC = b. Đường cao AH = h. Khi đó: SABCD=12(AB+CD)AH=12(a+b).h
II. Các ví dụ
Ví dụ 1: Cho hình thang ABCD có , AB = 3cm, BC = 5cm, CD = 6cm. Tính diện tích hình thang.
Lời giải:
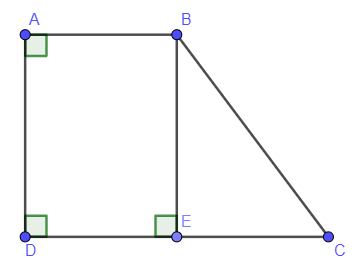
Kẻ BE vuông góc với CD tại E⇒^BED=90°
Xét tứ giác ABED có:
ˆA=ˆD=^BED=90°
⇒Tứ giác ABED là hình chữ nhật.
⇒AB = DE = 3cm (tính chất).
Ta có DC = DE + EC
⇒EC = DC – DE = 6 – 3 = 3cm
Xét tam giác BEC vuông tại E ta có:
BE2+EC2=BC2 (định lý Py – ta – go)
⇔BE2+32=52
⇔BE2=52−32
⇔BE2=25−9
⇔BE2=16
⇒BE=4cm
Diện tích hình thang ABCD là
SABCD=12(AB+CD).BE=12(3+6).4=18cm2.
Ví dụ 2: Cho hình thang cân ABCD (AB // CD, AB < CD). Biết AB = 10m, CD = 20cm, AD = 13cm. Tính diện tích hình thang ABCD.
Lời giải:

Kẻ AE vuông góc với CD tại E⇒^AEC=90°
Kẻ BF vuông góc với CD tại F⇒^BFD=90°
Vì {AE⊥CDBF⊥CD⇒AE//BF
Xét tứ giác ABFE có:
AE // BF (chứng minh trên)
AB // EF (do ABCD là hình thang và E, F thuộc CD)
Do đó tứ giác ABFE là hình bình hành
Lại có:^AEF=90° nên tứ giác ABFE là hình chữ nhật.
⇒AB=EF=10cm
Ta có: DE + EF + FC = DC
⇔DE + 10 + FC = 20
⇔DE + FC = 20 – 10 = 10 (1)
Vì ABCD là hình thang cân
⇒{ˆC=ˆDAD=BC(tính chất)
Xét tam giác AED và tam giác BFC có:
^AED=^BFC=90°
ˆC=ˆD(chứng minh trên)
AD = BC (chứng minh trên)
Do đó ΔAED=ΔBFC (cạnh huyền – góc nhọn)
⇒ED=CF(hai cạnh tương ứng) (2)
Từ (1) và (2)⇒ED=CF=5cm
Xét tam giác AED vuông tại E ta có:
AE2+ED2=AD2(định lý Py – ta – go)
⇔AE2+52=132
⇔AE2+25=169
⇔AE2=169−25
⇔AE2=144
⇒AE=12cm
Diện tích hình thang ABCD là:
SABCD=12(AB+CD).AE=12(10+20).12=180cm2
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.