Phương pháp giải Công thức tính diện tích tam giác (50 bài tập minh họa)

Bạn cần đăng nhập để đánh giá tài liệu

Phương pháp giải Công thức tính diện tích tam giác (50 bài tập minh họa)

Ngọc Nguyễn Ngày: 13-07-2023 Lớp 8

204

Toptailieu biên soạn và giới thiệu Phương pháp giải Công thức tính diện tích tam giác (50 bài tập minh họa) gồm các dạng bài tập có phương pháp giải chi tiết và các bài tập điển hình từ cơ bản đến nâng cao giúp học sinh biết cách làm các dạng toán.

Nội dung bài viết

I. Lý thuyết
II. Các ví dụ

Phương pháp giải Công thức tính diện tích tam giác (50 bài tập minh họa)

I. Lý thuyết

+ Tam giác thường:

Diện tích tam giác bằng nửa tích một cạnh với chiều cao tương ứng.

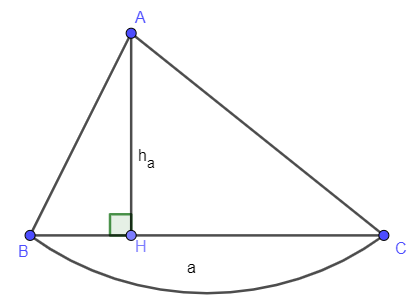
Phương pháp giải Công thức tính diện tích tam giác (50 bài tập minh họa) (ảnh 1)

S = $\frac{1}{2} a . h_{a}$ (đơn vị diện tích)

Với a là độ dài cạnh BC; $h_{a}$ là độ dài đường cao tương ứng với cạnh BC.

+ Tam giác vuông

Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông

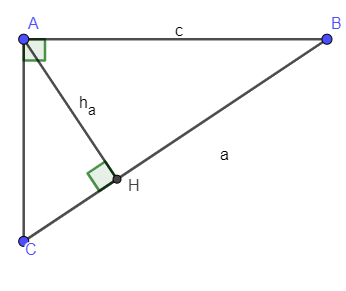
Phương pháp giải Công thức tính diện tích tam giác (50 bài tập minh họa) (ảnh 2)

Cho tam giác ABC vuông tại A có AB = c; AC = b; BC = a; đường cao AH = $h_{a}$

Diện tích tam giác vuông ABC: S = $\frac{1}{2} a h_{a} = \frac{1}{2} b c$ (đơn vị diện tích).

II. Các ví dụ

Ví dụ 1: Cho tam giác ABC vuông tại A có BC = 10cm; AC = 6cm. Tính diện tích tam giác ABC.

Lời giải:

Áp dụng định lí Py – ta – go cho tam giác vuông ABC ta có:

$A B^{2} + A C^{2} = B C^{2}$

$\Leftrightarrow A B^{2} + 6^{2} = 10^{2}$

$\Leftrightarrow A B^{2} + 36 = 100$

$\Leftrightarrow A B^{2} = 100 - 36$

$\Leftrightarrow A B^{2} = 64$

$\Rightarrow A B = 8$ cm.

Diện tích tam giác vuông ABC là:

$S_{A B C} = \frac{1}{2} . A B . A C = \frac{1}{2} .6.8 = 24 c m^{2}$

Ví dụ 2: Cho tam giác ABC, AB = AC = 10cm, BC = 12cm. Tính đường cao BK của tam giác ABC.

Lời giải:

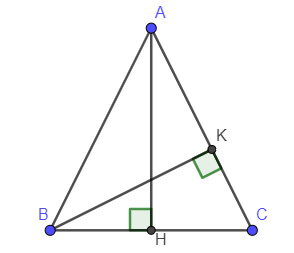
Phương pháp giải Công thức tính diện tích tam giác (50 bài tập minh họa) (ảnh 3)

Gọi H là chân đường cao kẻ từ A xuống BC.

Xét tam giác ABC có:

AB = AC = 10cm

$\Rightarrow$ Tam giác ABC cân tại A.

Do đó AH vừa là đường cao vừa là đường trung tuyến.

$\Rightarrow$ H là trung điểm của BC

$\Rightarrow$ HB = HC = $\frac{1}{2} B C$ = 6cm.

Xét tam giác AHB vuông tại H ta có:

$A H^{2} + B H^{2} = A B^{2}$ (định lý Py – ta – go)

$\Leftrightarrow A H^{2} + 6^{2} = 10^{2}$

$\Leftrightarrow A H^{2} = 10^{2} - 6^{2}$

$\Leftrightarrow A H^{2} = 100 - 36$

$\Leftrightarrow A H^{2} = 64$

$\Rightarrow A H = 8 c m$

Diện tích tam giác ABC là:

$S_{A B C} = \frac{1}{2} A H . B C = \frac{1}{2} 8.12 = 48 c m^{2}$

Mặt khác: $S_{A B C} = \frac{1}{2} B K . A C$

$\Rightarrow \frac{1}{2} B K .10 = 48$

$\Rightarrow 5 B K = 48$

$\Rightarrow B K = 48 : 5$

$\Rightarrow B K = 9,6 c m$ .

Ví dụ 3: Tìm diện tích lớn nhất của tam giác ABC biết AB = 3cm, BC = 4cm.

Lời giải:

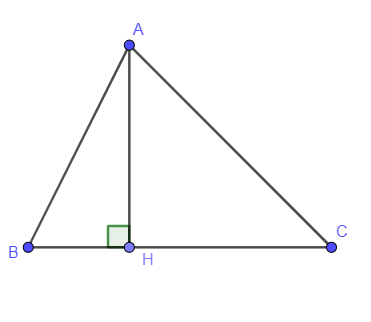
Tài liệu VietJack

Vẽ AH vuông góc với BC tại H

Theo quan hệ đường vuông góc và đường xiên ta có:

$A H \leq A B$

Khi đó diện tích tam giác ABC là

$S_{A B C} = \frac{1}{2} A H . B C \leq \frac{1}{2} A B . B C$

$\Rightarrow S_{A B C}$ lớn nhất khi $S_{A B C} = \frac{1}{2} A B . B C$

Dấu “=” xảy ra khi AH $\equiv$ AB hay H $\equiv$ B, tam giác ABC vuông tại B

Diện tích lớn nhất của tam giác ABC là:

$S_{A B C} = \frac{1}{2} A B . B C = \frac{1}{2} 3.4 = 6 c m^{2}$

Từ khóa :

Giải bài tập Toán 8

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

401

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

431

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

439

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

389