Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Công thức tính tiêu cự (50 bài tập minh họa) hay, chi tiết nhất, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức, từ đó học tốt môn Vật lí 11.

Phương pháp giải Công thức tính tiêu cự (50 bài tập minh họa)

1. Định nghĩa

Tiêu cự là độ dài đại số, kí hiệu là f, có trị số tuyệt đối bằng khoảng cách từ quang tâm O đến tiêu điểm chính của thấu kính, có đơn vị là cm hoặc m.

|f| = OF = OF’

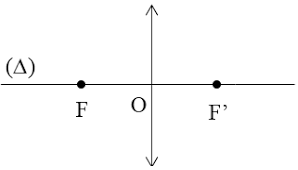
Thấu kính hội tụ

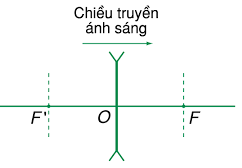
Thấu kính phân kỳ

Quy ước: f > 0 với thấu kính hội tụ; f < 0 với thấu kính phân kì.

2. Công thức – đơn vị đo

Khi đặt vật sáng trước thấu kính, ta thu được ảnh của vật. Khi biết vị trí ảnh và vật, ta có thể xác định tiêu cự của thấu kính bởi công thức:

$\frac{1}{f}=\frac{1}{d}+\frac{1}{d\text{'}}\iff \mathrm{f}=\frac{d.d\text{'}}{d+d\text{'}}$

Trong đó:

+ f là tiêu cự của thấu kính, có đơn vị cm hoặc m. Đối với thấu kính hội tụ f >0; đối với thấu kính phân kì f < 0.

+ d là khoảng cách từ vật đến thấu kính, có đơn vị cm hoặc m. Nếu vật thật d > 0; nếu vật ảo d < 0.

+ d’ là khoảng cách từ ảnh đến thấu kính, có đơn vị cm hoặc m. Nếu ảnh thật d’ > 0; nếu ảnh ảo d’ < 0.

Khi biết độ tụ của thấu kính, ta có thể tính tiêu cự bằng công thức

f = $\frac{1}{D}$

Trong đó:

+ D là độ tụ, có đơn vị đi ốp (kí hiệu là dp); D > 0 với thấu kính hội tụ; D < 0 với thấu kính phân kì.

+ f là tiêu cự, có đơn vị là mét (m).

Thấu kính hội tụ có khả năng hội tụ chùm sáng càng mạnh khi f càng nhỏ.

3. Mở rộng

3.1. Riêng với thấu kính mỏng, khi biết các bán kính cong của thấu kính, ta có thể tính tiêu cự bởi công thức:

$\frac{1}{f}=(n-1).\left(\frac{1}{R_1}+\frac{1}{R_2}\right)$

Trong đó:

+ f là tiêu cự, f > 0 với thấu kính hội tụ; f < 0 với thấu kính phân kì. Đơn vị đo của f là mét hoặc dm, cm.

+ n là chiết suất tỉ đối của vật liệu làm thấu kính với môi trường xung quanh thấu kính.

+ R₁ và R₂ là các bán kính của các mặt thấu kính, với quy ước

R₁, R₂ > 0 đối với các mặt lồi,

R₁, R₂ < 0 đối với các mặt lõm,

R₁, R₂ = 0 đối với các mặt phẳng.

3.2. Với hệ hai thấu kính mỏng đồng trục ghép sát, ta có thể xác định tiêu cự của thấu kính tương đương bởi công thức:

$\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}$ 

Trong đó:

+ f là tiêu cự thấu kính tương đương, có đơn vị m;

+ f₁ và f₂ lần lượt là tiêu cực của các thấu kính trong hệ ghép sát đồng trục, có đơn vị m.

3.3. Với mắt người bình thường, vật sáng ở trước mắt luôn cho ảnh hiện trên võng mạc, nên tiêu cự của thể thủy tinh được xác định bằng công thức

$\frac{1}{f}=\frac{1}{d}+\frac{1}{OV}$

4. Bài tập ví dụ

Bài 1: Một kính lão có ghi độ tụ là - 2 dp. Tính tiêu cự của kính?

Bài giải:

Áp dụng công thức $\mathrm{f}=\frac{1}{D}=\frac{1}{-2}=-0,5$  (m)

Đây là thấu kính phân kì có tiêu cự f = - 0,5 m

Đáp án: f = - 0,5 m

Bài 2: Một vật sáng AB đặt trước thấu kính và cách thấu kính 20 cm, cho ảnh ảo cách thấu kính 10 cm. Tính tiêu cự của kính. Đây là thấu kính loại gì?

Bài giải:

Vì vật thật nên d = 20 cm; ảnh ảo nên d’ = - 10 cm

Áp dụng công thức

$$\begin{gathered} \frac{1}{f}=\frac{1}{d}+\frac{1}{d\text{'}} \\ =>f=\frac{d.d\text{'}}{d+d\text{'}} \\ =\frac{20.(-10)}{20+(-10)}=-20 \left(cm\right) \end{gathered}$$

Đây là thấu kính phân kì.

Đáp án: f = - 20 cm

Bài 3: Một người mắt tốt có võng mạc cách mắt 2,5 cm có thể nhìn xa vô cùng mà không phải điều tiết. Khi đó tiêu cự của thể thủy tinh là bao nhiêu?

Bài giải:

Vì vật ở xa vô cùng nên d = ∞, ảnh thật hiện lên võng mạc nên d’ = 2,5 cm.

Ta có $$\begin{gathered} \frac{1}{f}=\frac{1}{d}+\frac{1}{d\text{'}}=\frac{1}{\infty }+\frac{1}{\mathrm{OV}} \\ =>f=\mathrm{OV} \end{gathered}$$

           = 2,5 cm.

Đây là trường hợp tiêu cự của mắt dài nhất.