Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Các dạng bài toán xác định nguyên tố thuộc 2 nhóm A liên tiếp trong Bảng HTTH (50 bài tập minh họa) hay, chi tiết nhất, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức, từ đó học tốt môn Hóa học 10.

Phương pháp giải Các dạng bài toán xác định nguyên tố thuộc 2 nhóm A liên tiếp trong Bảng HTTH (50 bài tập minh họa)

A. Phương pháp & Ví dụ

Lý thuyết và Phương pháp giải

Cần nhớ:

- Tổng số hiệu nguyên tử 4 < Z_T < 32 thì A, B sẽ thuộc các chu kỳ nhỏ hay Z_A - Z_B = 8.

- Nếu Z_T > 32 thì ta phải xét cả 3 trường hợp:

       + A là H.

       + A và B cách nhau 8 đơn vị.

       + A và B cách nhau 18 đơn vị.

Do hai nguyên tố thuộc cùng một nhóm nên tính chất tương tự nhau, vì vậy với những bài toán liên quan đến hỗn hợp phản ứng ta thay hỗn hợp bằng một công thức chung, sau đó tìm M− rồi chọn hau nguyên tố thuộc hau chu kì của cùng nhóm sao cho:

M_A < M− < M_B (M_A < M_B)

Ví dụ minh họa

Ví dụ 1: A và B là hai nguyên tố ở cùng một nhóm và thuộc hai chu kì liên tiếp trong bảng tuần hoàn. Tổng số proton trong hai hạt nhân nguyên tử của A và B bằng 32. Hãy viết cấu hình electron của A, B và của các ion mà A và B có thể tạo thành.

Hướng dẫn:

Theo bài ra, tổng số proton trong hai hạt nhân nguyên tử của A và B bằng 32 nên Z_A + Z_B = 32.

Trường hợp 1: Z_B - Z_A = 8. Ta tìm được Z_A = 12; Z_B = 20.

Cấu hình electron:

A : 1s²2s²2p⁶3s² (chu kỳ 3, nhóm IIA).

và B: 1s²2s²2p⁶3s²3p⁶4s² (chu kỳ 4, nhóm IIA).

Ion A²⁺: 1s²2s²2p⁶ và B²⁺: 1s²2s²2p⁶3s²3p⁶.

Trường hợp 2: Z_B - Z_A = 18. Ta tìm được Z_A = 7; D = 25.

Cấu hình electron:

A : 1s²2s²2p³ (chu kỳ 2, nhóm VA).

và B: 1s²2s²2p⁶3s²3p⁶3d⁵4s² (chu kỳ 4, nhóm VIIB).

Trường hợp này A, B không cùng nhóm nên không thỏa mãn.

Ví dụ 2. Cho 8,8 gam một hỗn hợp hai kim loại nằm ở hai chu kì liên tiếp nhau và thuộc nhóm IIIA, tác dụng với HCl dư thì thu được 6,72 lít khí hidro (đktc). Dựa vào bảng tuần hoàn cho biết tên hai kim loại đó.

Hướng dẫn:

Kí hiệu hai kim loại nhóm IIIA là M, nguyên tử khối trung bình là M−

Phương trình hóa học có dạng: 2M + HCl → 2MCl₂ + 3H₂

n_H2 = 6,72/22,4 = 0,3 (mol)

n_M = 2/3 n_H2 = 0,2 (mol)

theo đầu bài: M− .0,2 = 8,8 → M− = 44

hai kim loại thuộc hai chu kì liên tiếp, một kim loại có nguyên tử khối nhỏ hơn 44 và một kim loại có nguyên tử khối lơn hơn 44.

Dựa vào bảng tuần hoàn, hai kim loại đó là:

Al (M = 27 < 44) và Ga (M = 69,72 > 44).

Ví dụ 3: Hòa tan 20,2 gam hỗn hợp hai kim loại nằm ở hai chu kì liên tiếp thuộc nhóm IA trong bảng tuần hoàn tác dụng với nước thu được 6,72 lít khí (đktc) và dung dịch A. Xác định tên và khối lượng hai kim loại.

Hướng dẫn:

Gọi R là kí hiệu chung của hai kim loại nhóm IA, R cũng là nguyên tử khối trung bình của hai kim loại.

2R + 2H₂O → 2ROH + H₂ ↑

0,6                                  0,3

n_H2 = 6,72/22,4 = 0,3 (mol)

R = 20,2/0,6 = 33,67

Vì hai kim loại thuộc hai chu kì liên tiếp nên một kim loại phải có nguyên tử khối nhỏ hơn 33,67 và kim loại còn lại có nguyên tử khối lớn hơn 33,67.

Vậy ta có: R₁ = 23 (Na) < R = 33,67 < R₂ = 39 (K)

Dựa vào bảng tuần hoàn hai kim loại đó là Na, K

2Na + 2H₂O → 2NaOH + H₂ ↑

x                                        x/2

2K + 2H₂O → 2KOH + H₂ ↑

y                                       y/2

Ta có hệ phương trình:

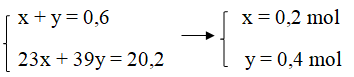
m_Na = 23.0,2 = 4,6 (gam)

m_K = 39.0,4 = 15,6 (gam)

B. Bài tập trắc nghiệm

Câu 1. Hòa tan 5,6 gam hỗn hợp hai kim loại X và Y thuộc nhóm IA vào 174,7 gam nước thu được 180 gam dung dịch A. Xác định tên kim loại X và Y. Biết chúng ở hai chu kì liên tiếp.

Lời giải:

Đáp án:

Đặt M− là khối lượng nguyên tử trung bình của hai kim loại.

2M− + 2H₂O → 2M−OH + H₂ (1)

0,3                    0,3        0,15

Áp dụng định luật bảo toàn khối lượng:

m_hh + m_H2O = m_ddA + m_H2 → m_H2 = 5,6 + 174,7 - 180 = 0,3 (gam)

→n_H2 = (0,3 )/2 = 0,15 (mol)

Theo (1): n_M− = 0,3 mol → M− = 5,6/0,3 = 18,67

Vì hai kim loại ở hai chu kì liên tiếp nên X là Li (M_X = 7), Y là n_A ( M_Y = 23)

Câu 2. Biết rằng X, Y là hai nguyên tố thuộc cùng một phân nhóm chính ở hai chu kì liên tiếp trong bảng tuần hoàn các nguyên tố, có tổng số proton trong hai hạt nhân là 32. Hãy viết cấu hình electron của nguyên tử X và Y.

Lời giải:

Đáp án:

Gọi Z_X, Z_Y lần lượt là số proton của nguyền tố X và Y.

Theo đề bài, ta có: Z_X + Z_Y = 32 (1)

Vì X, Y ở cùng phân nhóm chính và ở 2 chu kì kế tiếp nhau nên số proton của nhúng khác nhau hoặc là 8; 18, 32 đơn vị. Do đó xét 3 trường hợp sau. Giả sử Z_Y > Z_X

Trường hợp 1: Z_Y - Z_X = 8 (2)

Giải (1) và (2) ⇒ Z_X = 12 ; Z_Y = 20

Cấu hình electron của (X): ls²2s²2p⁶3s²

Cấu hình electron của (Y): ls²2s²2p⁶3s²3p⁶4s²

Phù hợp với đề bài (2 chu kì liên tiếp và ở phân nhóm chính) nên nhận.

Trường hợp 2: Z_Y - Z_X = 18 (3)

Giải (1) và (3) ⇒ Z_X = 7 ; Z_Y = 25

Vậy: Cấu hình electron của..(X): ls²2s²2p³ thuộc chu kì 2

Cấu hình electron của (Y): ls²2s²2p⁶3s²3p⁶4s²3d⁵: thuộc chu kì 4. Vậy laoij trường hợp này vì không thỏa mãn điều kiện đề bài.

Trường hợp 3: Z_Y - Z_X = 32 (3)

Giải (1) và (4) ⇒ Z_Y= 32 ; Z_X = 0 (loại)

Vậy nhận trường hợp 1.

Câu 3. Hỗn hợp A gồm 2 kim loại X, Y thuộc hai chu kì liên tiếp ở phân nhóm IIA. Cho 2,64 gam A tác dụng hết với dung dịch H₂SO₄ loãng thu được 2,016 khí (đktc). Xác định X, Y.

Lời giải:

Đáp án:

Thay thế hỗn hợp kim loại bằng một kim loại tương đương M−.

Số mol H₂ = 0,09 (mol)

       M− + H₂SO₄ → M ̅SO₄ + H₂

(mol) 0,09              ← 0,09

⇒ M− = 2,64/0,09 = 29,33

⇒ Mg = 24 < 29,33 < 40 = Ca

X, Y là Mg, Ca.

Câu 4. Hòa tan hoàn toàn 6,645 gam hỗn hợp muối clorua của hai kim loại kiềm thuộc hai chu kì kế tiếp nhau vào nước được dung dịch X. Cho toàn bộ dung dịch X tác dụng hoàn toàn với dung dịch AgNO₃ (dư), thu được 18,655 gam kết tủa. Tìm 2 kim loại kiềm.

Lời giải:

Đáp án:

Ta có: n_NaCl = 18,655/143,5=0,13 mol

M−Cl + AgNO₃ → M−NO₃ + AgCl

0,13 mol                          0,13 mol

⇒ (M− + 35,5).0,13 = 6,645 → M− = 15,62

Mà 2 kim loại kiềm thuộc hai chu kì kế tiếp nhau → Li (7) và Na(23)

Câu 5. A, B là 2 kim loại nằm ở hai chu kì liên tiếp thuộc nhóm IIA. Cho 4,4 gam một hỗn hợp gồm A và B tác dụng với HCl 1M (dư) thu được 3,36 lít khí (đktc).

a) Viết các phương trình phản ứng và xác định tên hai kim loại trên.

b) Tính thể tích dung dịch HCl đã dùng, biết rằng HCl dùng dư 25% so với lượng cần thiết.

Lời giải:

Đáp án:

a) Gọi công thức chung của hai kim loại là M

M + 2HCl → M_Cl2 + H₂

n_M = n_H2 = 0,15

Ta có: M_A = 4,4 → M = 4,4/0,15 = 29,33

A và B là 2 kim loại nằm ở 2 chu kì liên tiếp thuộc nhóm IIA nên A là Mg và B là Ca.

b) n_HCl = 0,15.2= 0,3 mol ⇒ V_HCl = 0,3/1 =0,3 lít = 300 ml.

V_{HCl đã dùng} = 300 + 25%.300 = 375 ml.

Câu 6. Cho 10,2 gam hỗn hợp hai kim loại thuộc nhóm IA và ở hai chu kì liên tiếp trong bảng tuần hoàn, tác dụng với H₂O dư thu được 5,6 lít khí H₂ (đktc). Xác định tên của hai kim loại đem dùng.

Lời giải:

Đáp án:

Gọi kim loại thuộc hai chu kì liên tiếp và thuộc nhóm IA là: X và Y (M_X < M_Y).

Gọi kim loại chung của hai kim loại này là : A−

      2A− + 2H₂O → 2A−OH + H₂ ↑ (1)

(mol) 0, 5        ←             0, 25

Ta có: n_H2 = 5,6/22,4 = 0,25 (mol). Từ (1) ⇒ n_A = 0, 5(mol)

M_A = (10,2)/0,5 = 20, 4 ⇒ M_X < M_A = 20, 4 < M_Y

Vậy X là Li (M = 7) và Y là n_A ( M = 23)

Câu 7. Cho 6,6 gam một hỗn hợp hai kim loại thuộc nhóm IIA và thuộc hai chu kì liên tiếp nhau tác dụng với dung dịch HCl dư thu được 5,04 lít khí H₂ (đktc). Hãy xác định hai kim loại trên.

Lời giải:

Đáp án:

Gọi kim loại thứ nhất là A và kim loại thứ hai là B, giả sử M_A < M_B.

Vì A, B đều thuộc nhóm IIA nên đều có hóa trị II

⇒ Gọi kim loại chung cho hai kim loại trên là M− (Với M_A < M− < M_B)

Ta có: n_H2 = 5,04/22,4 = 0,225 (mol)

Phản ứng: M− + 2HCl → M−Cl₂ + H₂ ↑ (1)

      mol 0,225        ← 0,225

Từ (1) ⇒ n_M− = M− × 0,225 = 6,6 ⇒ M− = 29,33

Dựa vào bảng tuần hoàn ⇒ Cặp nghiệm duy nhất là: A(Mg) và B(Ca).

Câu 8. X và Y là hai nguyền tố thuộc hai chu kì liên tiếp nhau và cùng thuộc một nhóm A, trong đó X có điện tích hạt nhân nhỏ hơn Y. Tổng số proton trong hạt nhân nguyên tử của X và Y là 22. Xác định hai nguyên tố X, Y.

Lời giải:

Đáp án:

Theo đề bài, ta có: Z_X + Z_Y = 22 (1)

Nếu X, Y thuộc hai chu kì nhỏ thì (Z_X < Z_Y): Z_Y = Z_X + 8 (2)

Từ (1) và (2) ⇒ Z_X = 7; Z_Y = 15.

Vậy X là N, Y là P.

Nếu X thuộc chu kì nhỏ và Y thuộc chu kì lớn thì: Z_Y = Z_X + 18 (3)

Từ (1) và (3) ⇒ Z_X = 2; Z_Y = 20 (loại vì không thảo mãn đề bài).

Nếu X, Y thuộc hai chu kì lớn: Z_Y = Z_X + 32 (4)

Từ (1) và (4) ⇒ Z_X < 0 (loại)