Cho hàm số y = x3 + 4x2 – 3x + 4. Khi đó:
A. Hàm số đạt cực đại tại x = \(\frac{1}{3}\), giá trị cực đại là \(\frac{{94}}{{27}}\).
B. Hàm số đạt cực đại tại x = −3, giá trị cực đại là 22.
C. Hàm số đạt cực đại tại x = 0, giá trị cực đại là 4.
D. Hàm số không có cực đại.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Tập xác định: D = ℝ.
Ta có: y = x3 + 4x2 – 3x + 4
y' = 3x2 + 8x – 3
y' = 0 ⇔ x = \(\frac{1}{3}\) hoặc x = −3.
Bảng biến thiên:
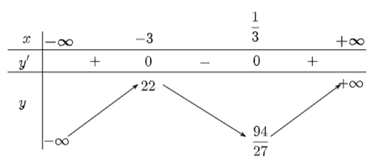
Hàm số đạt cực đại tại x = −3, giá trị cực đại là 22.
Hàm số đạt cực tiểu tại x = \(\frac{1}{3}\), giá trị cực tiểu là \(\frac{{94}}{{27}}\).
Giải SBT Toán 12 Chân trời sáng tạo Bài 1. Tính đơn điệu và cực trị của hàm số có đáp án
Cho hàm số y = 2x3 – 5x2 – 24x – 18.
a) Hàm số có hai cực trị.
b) Hàm số đạt cực đại tại x = \( - \frac{4}{3}\), giá trị cực đại là \(\frac{{10}}{{27}}\).
c) Hàm số đồng biến trên khoảng (3; +∞).
d) Hàm số đồng biến trên khoảng \(\left( { - \frac{4}{3};3} \right)\).
Đồ thị hàm số y = \(\frac{{{x^2} - 2x}}{{x + 1}}\) có hai trục đối xứng là hai đường phân giác của các góc tạo bởi hai đường thẳng:
a) x = 1 và y = x – 3.
b) x = 1 và y = −x + 3.
c) x = −1 và y = x – 3.
d) x = −1 và y = x + 3.
Giá thành của một sản phẩm trong 6 tháng đầu năm thay đổi theo công thức P(t) = 2t3 – 33t2 + 168t + 137 với P tính bằng nghìn đồng và t là số tháng tính từ đầu năm. Trong khoảng thời gian nào thì giá của sản phẩm tăng?
Hằng tháng, một công ty chuyên sản xuất mặt hàng A phải trả chi phí cố định là 50 triệu đồng (để thuê mặt bằng và lương nhân viên) và chi phí cho nguyên liệu là 10 000x (đồng) với x là số lượng sản phẩm A được nhập về.
a) Viết công thức tính chi phí trung bình \(\overline C (x)\) mà công ty cần chi phí để sản xuất một sản phẩm.
b) Tìm các tiệm cận của đồ thị hàm số \(\overline C (x)\).
Khảo sát và vẽ đồ thị của các hàm số sau:
a) y = x(x2 – 4x);
b) y = −x3 + 3x2 – 2.
Cho hàm số y = 2x3 + 6x2 – x + 2. Viết phương trình tiếp tuyến của đồ thị hàm số tại tâm đối xứng của nó.
Khảo sát và vẽ đồ thị của các hàm số sau:
a) y = 3 + \(\frac{1}{x}\);
b) y = 2 – \(\frac{1}{{1 + x}}\).
Quan sát Hình 1 và trả lời các câu hỏi từ 1 đến 3.
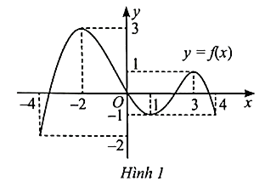
Hàm số y = f(x) trong Hình 1 nghịch biến trên khoảng nào?
A. (−2; 1).
B. (−4; −2).
C. (−1; 3).
D. (1; 3).
Quan sát Hình 1 và trả lời các câu hỏi từ 1 đến 3.

Hàm số y = f(x) trong Hình 1 có bao nhiêu điểm cực trị?
A. 2.
B. 3.
C. 4.
D. 5.
Đồ thị đạo hàm f'(x) của hàm số y = f(x) được cho trong Hình 2.
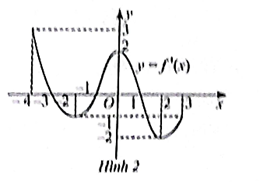
Điểm cực tiểu của hàm số y = f(x) là:
A. x = −3.
B. x = −1.
C. x = 0.
D. x = 1.
Đồ thị đạo hàm f'(x) của hàm số y = f(x) được cho trong Hình 3.
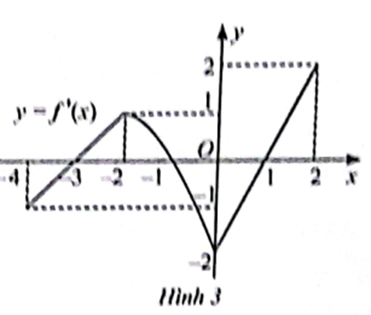
Hàm số y = f(x) đồng biến trên các khoảng
A. (−4; −2) và (−2; 2).
B. (−2; 0).
C. (−4; −3) và (−1; 1).
D. (−3; −1) và (1; 2).
Cho hàm số y = x3 – 12x + 6. Giá trị lớn nhất của hàm số trên đoạn [−3; 3] là
A. 6.
B. 15.
C. 17.
D. 22.
Cho hàm số y = \(\frac{{{x^2} - 2x + 6}}{{x + 1}}\).
A. Đồ thị hàm số có một tiệm cận xiên là y = x – 3.
B. Đồ thị hàm số có một tiệm cận xiên là y = x + 3.
C. Đồ thị hàm số có một tiệm cận xiên là y = x +1.
D. Đồ thị hàm số không có tiệm cận xiên.
Đồ thị hàm số y = \(\frac{{ - 4x + 3}}{{2x + 2}}\) có tâm đối xứng là điểm:
A. (−1; −2).
B. (−2; −1).
C. (−1; −1).
D. (−2; −2).
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.