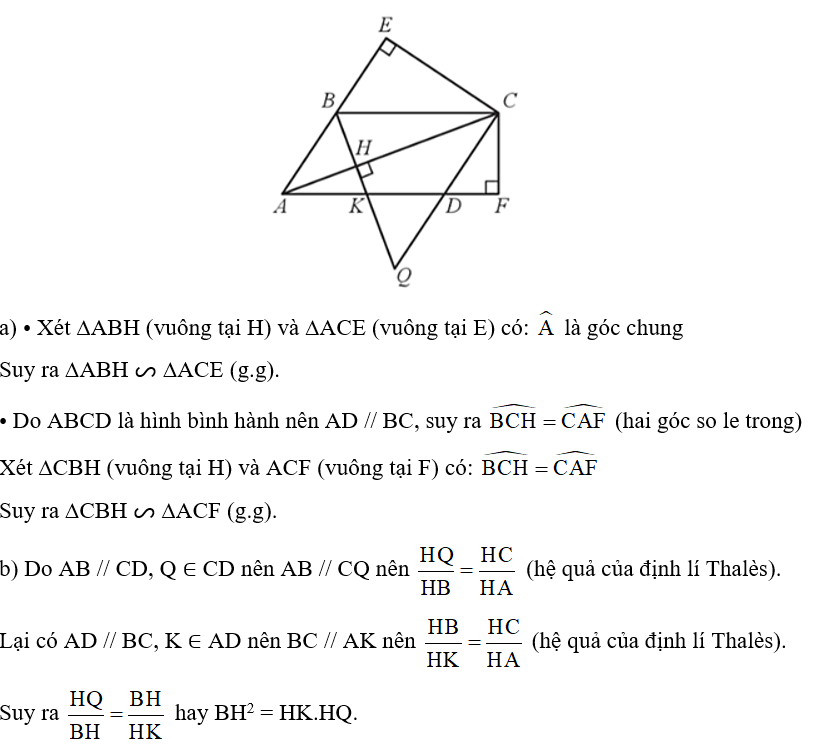
Cho hình bình hành ABCD (AC > BD). Vẽ CE vuông góc với đường thẳng AB tại E, CF vuông góc với đường thẳng AD tại F, BH vuông góc với đường thẳng AC tại H. Chứng minh:

a) ∆ABH ᔕ ∆ACE; ∆CBH ᔕ ∆ACF.

b) BH² = HK.HQ, biết tia BH cắt dường thẳng CD tại Q; cắt cạnh AD tại K.

∆ABC ᔕ ∆DEF theo tỉ số đồng dạng k, ∆MNP ᔕ ∆DEF theo tỉ số đồng dạng q. Khi đó, ∆ABC ᔕ ∆MNP theo tỉ số đồng dạng là:

A. k + q.

B. kq.

C. $\frac{q}{k}.$

D. $\frac{k}{q}.$

Cho hình thang ABCD, AB // CD, $\widehat{DAB}=\widehat{DBC},$ $\frac{AB}{BD}=\frac{2}{5}.$ Tính diện tích tam giác BDC, biết diện tích tam giác ABD là 44,8 cm2.

Cho tam giác ABC có ba góc nhọn, điểm I thuộc cạnh BC và IM, IN lần lượt là đường phân giác của các góc AIC và AIB. Chứng minh: AN.BI.CM = BN.IC.AM.

Để đo khoảng cách AB, trong đó điểm B không tới được, người ta tiến hành đo bằng cách lấy các điểm C, D, E sao cho AD = 10 m, CD = 7 m, DE = 4 m (Hình 57). Khi đó, khoảng cách AB (tính theo đơn vị mét và làm tròn kết quả đến hàng phần mười) là:

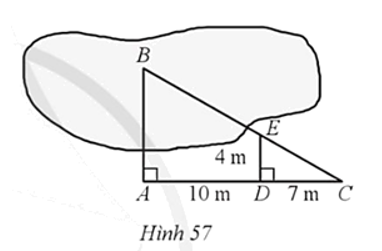
A. 9,3 m.

B. 9,4 m.

C. 9,6 m.

D. 9,7 m.

Cho tam giác ABC, điểm M thuộc cạnh BC sao cho MC = 2MB. Đường thẳng qua M song song với AC cắt AB ở D. Đường thẳng qua M song song với AB cắt AC ở E. Gọi x, y lần lượt là chu vi tam giác DBM và tam giác ECM. Tính x + 2y, biết chu vi tam giác ABC bằng 30 cm.

Cho tam giác ABC có ba góc nhọn, các đường cao BD và CE cắt nhau tại H. Chứng minh:

a) ∆EBH ᔕ ∆DCH, ∆ADE ᔕ ∆ABC;

b) DB là tia phân giác của góc EDI, với I là giao điểm của AH và BC.

Cho ∆MNP ᔕ ∆M’N’P’ và $\widehat{M}=30°,\widehat{N^{\text{'}}}=40°.$ Số đo góc P là:

A. 30°.

B. 40°.

C. 70°.

D. 110°.

Cho tam giác ABC có BD là đường phân giác của góc ABC (Hình 56). Độ dài DC là:

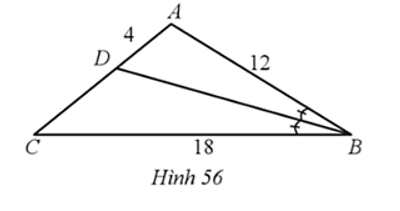
A. 6.

B. 9.

C. 5.

D. 8 .

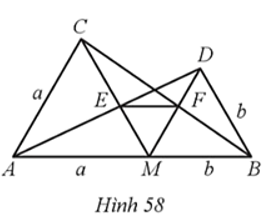
Cho điểm M thuộc đoạn thẳng AB, với MA = a, MB = b. Vẽ hai tam giác đều AMC và BMD; gọi E là giao điểm của AD và CM, F là giao điểm của DM và BC (Hình 58).

a) Chứng minh EF // AB.

b) Tính ME, MF theo a, b.

Cho tam giác ABC. Các điểm M, N lần lượt thuộc các cạnh AB và AC thỏa mãn MN // BC và $\frac{AM}{MB}=\frac{2}{3}.$ Tỉ số $\frac{NC}{AN}$ bằng

Cho hai tam giác MNP và M’N’P’. Phát biểu nào sau đây là đúng?

A. Nếu $\widehat{M}=\widehat{M^{\text{'}}}$ và $\widehat{N}=\widehat{P^{\text{'}}}$ thì ∆MNP ᔕ ∆M’N’P’.

B. Nếu $\widehat{M}=\widehat{N^{\text{'}}}$ và $\widehat{N}=\widehat{P^{\text{'}}}$ thì ∆MNP ᔕ ∆M’N’P’.

C. Nếu $\widehat{M}=\widehat{P^{\text{'}}}$ và $\widehat{N}=\widehat{M^{\text{'}}}$ thì ∆MNP ᔕ ∆M’N’P’.

D. Nếu $\widehat{M}=\widehat{M^{\text{'}}}$ và $\widehat{P}=\widehat{P^{\text{'}}}$ thì ∆MNP ᔕ ∆M’N’P’.

Nếu ∆MNP ᔕ ∆DEG thì

Hình 54 cho biết A’B’ = 4, A’O = 3, AO = 6, OB = x, AB = y.

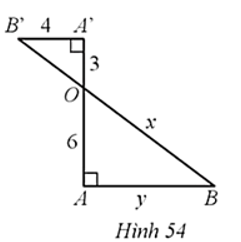
Giá trị của biểu thức x + y là:

A. 22.

B. 18.

C. 20.

D. 16.

Cho tam giác ABC có DE // BC (Hình 55).

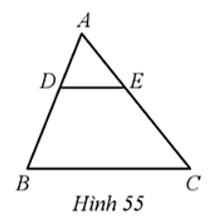
Khẳng định nào dưới đây đúng?