Chọn phương án đúng.
Cho tam giác ABC vuông tại A (AB ≠ AC) và tam giác DEF vuông tại D (DE ≠ DF). Điều nào dưới đây không suy ra ∆ABC ᔕ ∆DEF.
A. ˆB=ˆE.
B. ˆC=ˆF.
C. ˆB+ˆC=ˆE+ˆF.
D. ˆB−ˆC=ˆE−ˆF.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
Vì ˆB+ˆC=ˆE+ˆF chưa thể suy ra được ˆB=ˆE và ˆC=ˆF.
Vậy đáp án C không suy ra được ∆ABC ᔕ ∆DEF.
Giải VTH Toán 8 KNTT Bài tập cuối chương 9 có đáp án
Cho tam giác ABC có đường cao AH. Biết AH = 12 cm, CH = 9 cm, BH = 16 cm. Lấy M, N lần lượt là trung điểm của AH, BH (H.9.28).
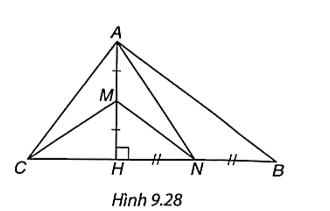
a) Chứng minh rằng ABC là tam giác vuông tại A.
b) Chứng minh rằng MN ⊥ AC và CM ⊥ AN.
c) Tính diện tích tam giác AMN.
Cho tam giác ABC vuông tại A có AB = 5 cm, AC = 4 cm. Gọi AH, HD lần lượt là các đường cao kẻ từ đỉnh A của tam giác ABC và đỉnh H của tam giác HAB.
a) Chứng minh rằng ∆HDA ᔕ ∆AHC.
b) Tính độ dài các đoạn thẳng HA, HB, HC, HD.
Chọn phương án đúng.
Cho ∆A'B'C' ᔕ ∆ABC. với tỉ số đồng dạng bằng 2. Khẳng định nào sau đây là đúng?
A. ABA'B'=2.
B. ABA'C'=2.
C. A'B'AB=2.
D. A'B'AC=2.
Chọn phương án đúng.
Trong các bộ ba số đo dưới đây, đâu là số đo ba cạnh của một tam giác vuông?
A. 3 m; 5 m; 6 m.
B. 6 m; 8 m; 10 m.
C. 1 cm; 0,5 cm; 1,25 cm.
D. 9 m; 16 m; 25 m.
Cho tam giác ABC vuông tại A và các điểm D, E, F như Hình 9.29 sao cho AD là phân giác của góc BAC, DE và DF lần lượt vuông góc với AC và BC.
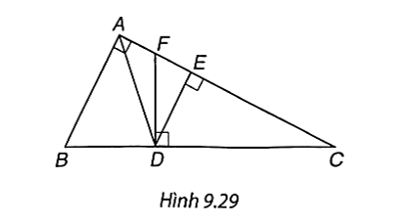
Chứng minh rằng:
a) BDBC=ABAB+AC, từ đó suy ra AE=AB.ACAB+AC;
b) ∆DFC ᔕ ∆ABC;
c) DF = DB.
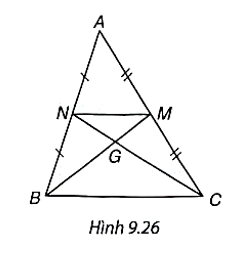
Hai đường trung tuyến BM, CN của tam giác ABC cắt nhau tại điểm G (H.9.26). Chứng minh rằng tam giác GMN đồng dạng với tam giác GBC và tìm tỉ số đồng dạng.
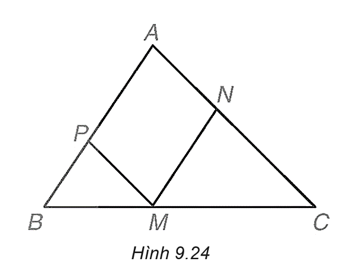
Cho Hình 9.24, biết rằng MN // AB, MP // AC. Hãy liệt kê ba cặp tam giác (phân biệt) đồng dạng có trong hình.
Chọn phương án đúng.
Cho ABC là tam giác không cân. Biết ∆A'B'C' ᔕ ∆ABC. Khẳng định nào sau đây là đúng?
A. ∆A'C'B' ᔕ ∆ACB.
B. ∆B'C'A' ᔕ ∆BAC.
C. ∆B'A'C' ᔕ ∆BCA.
D. ∆A’C'B' ᔕ ∆ABC.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.