Cho hình chóp S.ABCD đáy là hình bình hành. Gọi I, J lần lượt là trung điểm của SB, AB. Điểm M là một điểm bất kì trên nửa đường thẳng Ax chứa C. Biện luận theo vị trí của điểm M trên Ax các dạng của thiết diện của hình chóp cắt bởi mặt phẳng (IJM).
 Giải bởi Vietjack
Giải bởi Vietjack
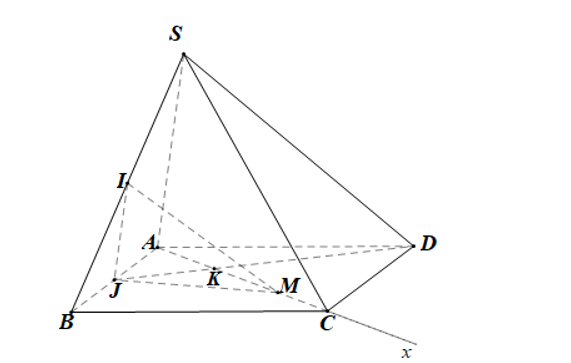
Gọi K là giao điểm của AC và JD.
Khi đó:
• Nếu M ∈ Cx thì thiết diện là hình tam giác;
• Nếu M ∈ KC thì thiết diện là hình tứ giác;
• Nếu M ∈ Cx thì thiết diện là hình ngũ giác.
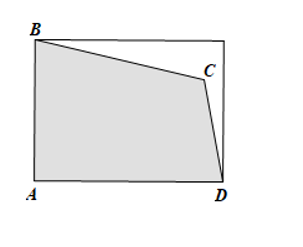
Một mảnh đất hình chữ nhật bị xén đi một góc (hình vẽ), phần còn lại có dạng hình tứ giác ABCD với độ dài các cạnh là AB = 15m, BC = 19m, CD = 10m, DA = 20m. Diện tích mảnh đất ABCD bằng bao nhiêu mét vuông (làm tròn kết quả đến hàng đơn vị).
Cho tứ diện đều ABCD cạnh a. Gọi I, J lần lượt là trung điểm của AC và BC. Gọi K là điểm trên cạnh BD với KB = 2KD. Thiết diện của tứ diện với mặt phẳng (IJK) là hình gì?
Cho tam giác ABC vuông tại A, đường cao AH. Biết ACAB=√2, HC – HB = 2. Tính:
a) Tỉ số HCHB.
b) AB, BC, CA.
Cho tam giác ABC nhọn nội tiếp đường tròn tâm O, bán kính R. Đường cao BD, CE cắt nhau tại H. Vẽ đường kính AF của đường tròn tâm O. Gọi I là trung điểm của BC.
a) Chứng minh H, I, F thẳng hàng.
b) Chứng minh AH = 2OI.
c) Gọi G là trọng tâm của tam giác ABC. Chứng minh SΔAHG=2SΔAGO.
Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC.
a) Chứng minh hai tam giác ABM và ACM bằng nhau.
b) Chứng minh AM vuông góc với BC.
c) Chứng minh AM là phân giác của góc A.
Diện tích hình bình hành bằng 24 cm2. Khoảng cách từ giao điểm hai đường chéo đến các cạnh hình bình hành bằng 2 cm và 3 cm. Tính chu vi của hình bình hành.
Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số: y = 4sin2x – 4sinx + 3.
Cho tam giác AEB vuông tại A, từ điểm C trên cạnh BE kẻ đường vuông góc với BE cắt tia đối của tia AB ở F, cắt AE ở D. Tia phân giác của góc E cắt AB, CD lần lượt ở M, P. Tia phân giác của góc F cắt BC, DA lần lượt ở N và Q. Chứng minh:
a) EM vuông góc với FN.
b) Tứ giác MPNQ là hình thoi.
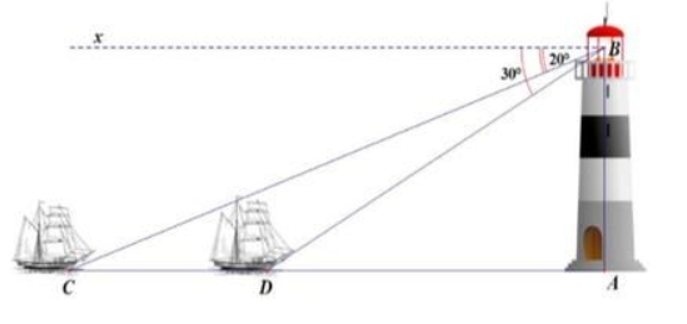
Một người đứng trên tháp quan sát của ngọn hải đăng cao 50 m nhìn về hướng Tây Nam, người đó quan sát hai lần một con thuyền đang hướng về ngọn hải đăng. Lần thứ nhất người đó nhìn thấy thuyền với góc hạ là 20°, lần thứ 2 người đó nhìn thấy thuyền với góc hạ là 30°. Hỏi con thuyền đã đi được bao nhiêu mét giữa hai lần quan sát? (làm tròn đến chữ số thập phân thứ nhất)
Cho hàm số y = (2 – m)x + 3.
a) Tìm m để (d) đi qua điểm A(2; 3).
b) Tìm m để (d) cắt trục hoành tại điểm có hoành độ là –1.
c) Tìm m để (d) cắt trục tung tại điểm có tung độ là 3.
Cho biểu thức P=(1x−√x+1√x−1):√xx−2√x+1 .
a) Rút gọn biểu thức P.
b) Tìm các giá trị của x để P>12 .
Cho đường tròn (O; R) và điểm A cố định ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên d lấy M. Qua M kẻ tiếp tuyến ME, MF với (O). Nối EF cắt OM tại H, cắt OA tại B.
a) Chứng minh tứ giác ABHM nội tiếp.
b) Chứng minh OA.OB = OH.OM = R2.
c) Chứng minh tâm I của đường tròn nội tiếp tam giác MEF thuộc một đường tròn cố định khi M di chuyển trên d.
d) Tìm vị trí của M để diện tích tam giác HBO lớn nhất.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.