Cho hình chữ nhật ABCD có hai đỉnh di động trên đồ thị hàm số y=9−x2 trên khoảng (−3;3), hai đỉnh còn lại nằm trên trục hoành (tham khảo hình vẽ). Tìm diện tích lớn nhất của hình chữ nhật ABCD (làm tròn kết quả đến hàng phần mười).
 Giải bởi Vietjack
Giải bởi Vietjack
Kí hiệu x là hoành độ của điểm B (0<x<3).
Ta có AB=2x,BC=9−x2.
Từ đó, diện tích hình chữ nhật ABCD là S(x)=18x−2x3,0<x<3.
Ta có S′(x)=18−6x2, S′(x)=0⇔x2=3⇔x=√3 (do x>0). Bảng biến thiên:
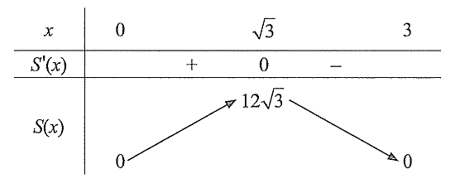
Từ đó max(0;3)S(x)=S(√3)=12√3≈20,8.
Đáp án: 20,8.
Đề thi ôn tốt nghiệp THPT Toán có lời giải ( Đề 5)
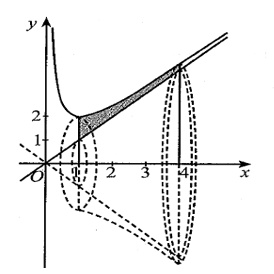
Một chiếc bát thủy tinh có bề dày của phần xung quanh là một khối tròn xoay, khi xoay hình phẳng D quanh một đường thẳng a bất kì nào đó mà khi gắn hệ trục tọa độ Oxy (đơn vị trên trục là decimét) vào hình phẳng D tại một vị trí thích hợp, thì đường thẳng a sẽ trùng với trục Ox. Khi đó hình phẳng D được giới hạn bởi các đồ thị hàm số y=x+1x, y=x và hai đường thẳng x=1, x=4. Thể tích của bề dày chiếc bát thủy tinh đó bằng bao nhiêu decimét khối (làm tròn kết quả đến hàng phần mười)?
Khi đặt hệ tọa độ Oxyzvào không gian với đơn vị trên trục tính theo kilômét, người ta thấy rằng một không gian phủ sóng điện thoại có dạng một hình cầu (S) (tập hợp những điểm nằm trong và nằm trên mặt cầu tương ứng). Biết mặt cầu (S) có phương trình: x2+y2+z2−2x−4y−6z+5=0. Khoảng cách xa nhất giữa hai vùng phủ sóng là bao nhiêu kilômét?
![Khi đặt hệ tọa độ \[Oxyz\]vào không gian với đơn vị trên trục tính theo kilômét, người ta thấy rằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid44-1737301480.png)
Xác suất bắn trúng đích của xạ thủ hạng I là 0,8 và của xạ thủ hạng II là 0,7. Chọn ngẫu nhiên 1 xạ thủ từ một nhóm gồm 4 xạ thủ hạng I và 6 xạ thủ hạng II. Xạ thủ này bắn một viên đạn và viên đạn đó trúng mục tiêu, tính xác suất để đó là xạ thủ hạng I (làm tròn kết quả đến hàng phần trăm).
Cho hàm số f(x)=2x−1x2+2.
a) Đồ thị hàm số y=f(x) nhận trục hoành làm tiệm cận ngang.
b) Hàm số f(x) có x=2 làm điểm cực tiểu.
c) Với mọi x∈R, ta luôn có −1≤f(x)≤12.
d) Nếu −1<m≤0 thì phương trình f(x)=m có hai nghiệm.
Trong không gian Oxyz, cho ba điểm A(−1;1;2),B(3;2;2),C(−1;6;0). Xét M(a;b;0) trên mặt phẳng (Oxy) sao cho biểu thức S=2MA+|→MB+→MC| đạt giá trị nhỏ nhất. Khi đó a+b bằng bao nhiêu (làm tròn kết quả đến hàng phần mười)?
Có bao nhiêu số nguyên a sao cho hàm số f(x)=x3+ax2+3x+1 đồng biến trên R?
Thời gian thực hiện xong một thí nghiệm hóa học của học sinh lớp 12H được ghi lại ở bảng sau:
|
Thời gian (phút) |
[5;6) |
[6;7) |
[7;8) |
[8;9) |
[9;10) |
|
Số học sinh |
12 |
25 |
0 |
0 |
1 |
Khoảng biến thiên của mẫu số liệu trên là
Trong không gian Oxyz, đường thẳng đi qua hai điểm A(−1;1;0) và B(3;2;−1) có phương trình tham số là
Trong không gian Oxyz, cho hai điểm A(1;2;3), B(0;1;−6) và mặt phẳng (P):4x−y+2z+13=0.
a) Mặt phẳng (P) đi qua điểm A.
b) Đường thẳng Δ đi qua điểm A và vuông góc với mặt phẳng (P) có phương trình tham số là {x=1+4ty=2+tz=3+2t.
c) Điểm C(−3;3;1) là giao điểm của đường thẳng Δ và mặt phẳng (P).
d) Gọi d là một đường thẳng nằm trong (P) và d đi qua B sao cho khoảng cách từ A đến d đạt giá trị nhỏ nhất. Một vectơ chỉ phương của d có tọa độ là (a;b;c) với a là số nguyên tố. Giá trị của a+b+c=6.
Huấn luyện viên thống kê thời gian chạy cự li 200 m của hai vận động viên Hoa và Mai trong một đợt huấn luyện ở bảng sau.
|
Thời gian (giây) |
[23,7;23,8) |
[23,8;23,9) |
[23,9;24) |
[24;24,1) |
[24,1;24,2) |
|
Số lần chạy của Hoa |
11 |
15 |
7 |
0 |
5 |
|
Số lần chạy của Mai |
28 |
18 |
4 |
0 |
0 |
a) Khoảng biến thiên thời gian chạy của hai vận động viên là như nhau.
b) Thành tích trung bình của Hoa đạt dưới 23,9 giây.
c) Nếu so sánh theo số trung bình thì thành tích của Hoa tốt hơn của Mai.
d) Nếu so sánh theo độ lệch chuẩn thì Mai có thành tích ổn định hơn Hoa.
Cho hàm số f(x) có bảng biến thiên như sau:
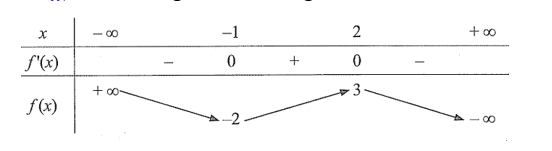
Giá trị cực đại của hàm số đã cho là
Trong không gian tọa độ Oxyz,vectơ nào sau đây là vectơ pháp tuyến của mặt phẳng (P):2x−y+z+3=0?
Biết hàm số F(x) là một nguyên hàm của hàm số f(x)=4x và F(1)=1ln2. Giá trị của F(32)⋅ln2 bằng
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.