Tìm tất cả các giá trị thực của tham số m để bất phương trình
f(x) = (m – 3)x2 + (m + 2)x – 4 > 0 vô nghiệm
C. – 22 < m < 2;
D. [−22≤m≤2m=3.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Ta có f(x) > 0 vô nghiệm ⇔f(x)≤0∀x∈R.
Xét m = 3 ta có f(x) = 5x – 4 với x>45 thì f(x) > 0 nên m = 3 không thỏa mãn.
Xét m ≠ 3 ta có f(x)≤0∀x∈R⇔{a=m−3<0Δ=m2+20m−44≤0⇔{m<3m2+20m−44≤0
Xét tam thức bậc hai (biến m): m2 + 20m – 44 có ∆’ = 102 – (-44) = 144 > 0. Do đó tam thức có hai nghiệm phân biệt x = -22 và x = 2.
Ta có bảng xét dấu

Để f(x)≤0∀x∈R⇔{m<3−22≤m≤2⇔−22≤m≤2
Vậy đáp án đúng là B.
Cho hàm số y = ax2 + bx + c có đồ thị như hình sau:
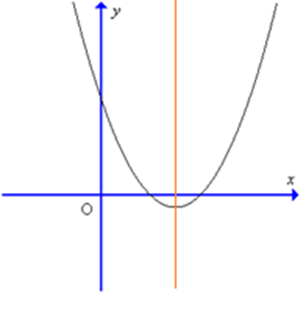
Kết luận nào sau đây đúng về hệ số a, b:
Cho f(x) = x2 – 1. Tìm khẳng định sai trong các khẳng định sau đây
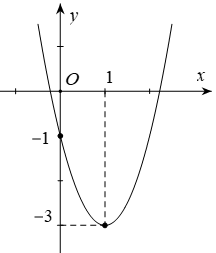
Cho parabol (P): y = ax2 + bx + c có đồ thị như hình bên. Phương trình của parabol này là :
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.