Toptailieu biên soạn và giới thiệu lời giải Toán 11 (Kết nối tri thức) Bài 11: Vị trí địa lí, điều kiện tự nhiên, dân cư, xã hội và kinh tế khu vực Đông Nam Á hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi SGK Toán 11 Bài từ đó học tốt môn Toán 11.

Toán 11 (Cánh diều) Bài tập cuối chương 6

Giải Toán 11 trang 56 Tập 2

Bài 1 trang 56 Toán 11 Tập 2: Điều kiện xác định của x^–3 là:

A. x∈ ℝ.

B. x ≥ 0.

C. x ≠ 0.

D. x > 0.

Lời giải:

Đáp án đúng là: C

Ta có $x^{–3}=\frac{1}{x^3}$

Khi đó hàm số $x^{–3}=\frac{1}{x^3}$ xác định ⇔ x ≠ 0.

Bài 2 trang 56 Toán 11 Tập 2: Điều kiện xác định của $x^{\frac{3}{5}}$ là:

A. x∈ ℝ.

B. x ≥ 0.

C. x ≠ 0.

D. x > 0.

Lời giải:

Đáp án đúng là: A

Ta có: $x^{\frac{3}{5}}=\sqrt[5]{x^3}$

Khi đó hàm số $x^{\frac{3}{5}}=\sqrt[5]{x^3}$ xác định với mọi x∈ ℝ.

Bài 3 trang 56 Toán 11 Tập 2: Tập xác định của hàm số y = log_0,5(2x – x²) là:

A. (–∞; 0) ∪ (2; +∞).

B. ℝ \{0; 2}.

C. [0; 2].

D. (0; 2).

Lời giải:

Đáp án đúng là: D

Hàm số y = log_0,5(2x – x²) xác định ⇔ 2x – x² > 0

⇔ x² – 2x < 0 ⇔ x(x – 2) < 0

⇔ 0 < x < 2.

Vậy tập xác định của y = log_0,5(2x – x²) là (0; 2).

Bài 4 trang 56 Toán 11 Tập 2: Hàm số nào sau đây đồng biến trên tập xác định của nó?

A. y = (0,5)^x.

B. $y={\left(\frac{2}{3}\right)}^x.$

C. $y={\left(\sqrt{2}\right)}^x.$

D. $y={\left(\frac{e}{\pi }\right)}^x.$

Lời giải:

Đáp án đúng là: C

Vì 0 < 0,5 < 1 nên hàm số y = (0,5)^x nghịch biến trên ℝ;

Vì $0<\frac{2}{3}<1$nên hàm số $y={\left(\frac{2}{3}\right)}^x$ nghịch biến trên ℝ;

Vì $\sqrt{2}>1$ nên hàm số $y={\left(\sqrt{2}\right)}^x$ đồng biến trên ℝ;

Vì $0<\frac{e}{\pi }<1$nên hàm số $y={\left(\frac{e}{\pi }\right)}^x$ nghịch biến trên ℝ.

Vậy ta chọn đáp án C.

Bài 5 trang 56 Toán 11 Tập 2: Hàm số nào sau đây nghịch biến trên tập xác định của nó?

A. y = log₃x.

B. $y={\log }_{\sqrt{3}}x$.

C. $y={\log }_{\frac{1}{e}}x$.

D. y = log_πx.

Lời giải:

Đáp án đúng là: C

Hàm số y = log_ax nghịch biến trên tập xác định của nó khi 0 < a < 1.

Mà $3>\mathrm{1,}\sqrt{3}>\mathrm{1,}\pi >\mathrm{1,0}<\frac{1}{e}<1$

Suy ra hàm số $y={\log }_{\frac{1}{e}}x$nghịch biến trên tập xác định của nó.

Bài 6 trang 56 Toán 11 Tập 2: Nếu 3^x = 5 thì 3^2x bằng:

A. 15.

B. 125.

C. 10.

D. 25.

Lời giải:

Đáp án đúng là: D

Ta có: 3^2x = (3^x)² = 5² = 25.

Bài 7 trang 56 Toán 11 Tập 2: Cho $A=4^{{\log }_{2}3}.$ Khi đó giá trị của A bằng:

A. 9.

B. 6.

C. $\sqrt{3}.$

D. 81.

Lời giải:

Đáp án đúng là: A

Ta có: $A=4^{{\log }_{2}3}=2^{2{\log }_{2}3}=2^{{\log }_2{3}^2}=3^2=9.$

Vậy ta chọn đáp án A.

Bài 8 trang 56 Toán 11 Tập 2: Nếu log_ab = 3 thì log_ab² bằng:

A. 9.

B. 5.

C. 6.

D. 8.

Lời giải:

Đáp án đúng là: C

Ta có: log_ab² = 2log_ab = 2 . 3 = 6.

Bài 9 trang 56 Toán 11 Tập 2: Nghiệm của phương trình 3^{2x – 5} = 27 là:

A. 1.

B. 4.

C. 6.

D. 7.

Lời giải:

Đáp án đúng là: B

Ta có: 3^{2x – 5} = 27 ⇔3^{2x – 5} = 3³ ⇔ 2x – 5 = 3 ⇔ x = 4.

Bài 10 trang 56 Toán 11 Tập 2: Nghiệm của phương trình log_0,5(2 – x) = –1 là:

A. 0.

B. 2,5.

C. 1,5.

D. 2.

Lời giải:

Đáp án đúng là: A

Ta có log_0,5(2 – x) = –1 ⇔ 2 – x = 0,5^–1 ⇔ 2 – x = 2 ⇔ x = 0.

Bài 11 trang 56 Toán 11 Tập 2: Tập nghiệm của bất phương trình (0,2)^x > 1 là:

A. (–∞; 0,2).

B. (0,2; +∞).

C. (0; +∞).

D. (–∞; 0).

Lời giải:

Đáp án đúng là: D

Ta có (0,2)^x > 1 ⇔ x < log_0,21 ⇔ x < 0.

Vậy bất phương trình đã cho có tập nghiệm là (–∞; 0).

Giải Toán 11 trang 57 Tập 2

Bài 12 trang 57 Toán 11 Tập 2: Tập nghiệm của bất phương trình ${\log }_{\frac{1}{4}}x>-2$ là:

A. (–∞; 16).

B. (16; +∞).

C. (0; 16).

D. (–∞; 0).

Lời giải:

Đáp án đúng là: C

Ta có ${\log }_{\frac{1}{4}}x>-2\iff 0<x<{\left(\frac{1}{4}\right)}^{-2}\iff 0<x<16$

Vậy bất phương trình đã cho có tập nghiệm là (0; 16).

Bài 13 trang 57 Toán 11 Tập 2: Cho ba số thực dương a, b, c khác 1 và đồ thị ba hàm số mũ y = a^x, y = b^x, y = c^x được cho bởi Hình 14.

Kết luận nào sau đây là đúng đối với ba số a, b, c?

A. c < a < b.

B. c < b < a.

C. a < b < c.

D. b < c < a.

Lời giải:

Đáp án đúng là: A

Từ các đồ thị hàm số trên Hình 14 ta thấy:

⦁ Hàm số y = c^x nghịch biến trên ℝ nên 0 < c < 1;

⦁ Hai hàm số y = a^x và y = b^x đồng biến trên ℝ nên a > 1 và b > 1.

Thay cùng giá trị của x = x₀ (với x₀ > 0) vào hai hàm số y = a^x và y = b^x ta thấy nên a < b

Suy ra c < a < b.

Bài 14 trang 57 Toán 11 Tập 2: Cho ba thực dương a, b, c khác 1 và đồ thị ba hàm số lôgarit y = log_ax, y = log_bx, y = log_cx được cho bởi Hình 15. Kết luận nào sau đây là đúng với ba số a, b, c?

A. c < a < b.

B. c < b < a.

C. a < b < c.

D. b < c < a.

Lời giải:

Đáp án đúng là: D

Từ các đồ thị hàm số trên Hình 15 ta thấy:

⦁ Hàm số y = log_ax đồng biến trên (0; +∞) nên a > 1;

⦁ Hai hàm số y = log_bx và y = log_cx nghịch biến trên (0; +∞) nên 0 < b < 1; 0 < c < 1.

Thay cùng giá trị của x = x₀ (với x₀ ∈ (0; +∞)) vào hai hàm số ta thấy log_bx₀ > log_cx₀

Mà 0 < b < 1; 0 < c < 1 nên b < c.

Suy ra b < c < a.

Bài 15 trang 57 Toán 11 Tập 2: Viết các biểu thức sau về lũy thừa cơ số a:

a) $A=\sqrt[3]{5\sqrt{\frac{1}{5}}}$với a = 5. b) $B=\frac{4\sqrt[5]{2}}{\sqrt[3]{4}}$ với $a=\sqrt{2}.$

Lời giải:

a) Ta có: $A=\sqrt[3]{5\sqrt{\frac{1}{5}}}=\sqrt[3]{5\cdot {\left(\frac{1}{5}\right)}^{\frac{1}{2}}}=\sqrt[3]{5\cdot 5^{-\frac{1}{2}}}$$=\sqrt[3]{5^{\frac{1}{2}}}=5^{\frac{1}{2}\cdot \frac{1}{3}}=5^{\frac{1}{6}}$

Vậy $A=a^{\frac{1}{6}}.$

b) $a=\sqrt{2}\Rightarrow a^2=2$

Ta có: $B=\frac{4\sqrt[5]{2}}{\sqrt[3]{4}}=\frac{2^2\cdot 2^{\frac{1}{5}}}{4^{\frac{1}{3}}}=\frac{2^{\frac{11}{5}}}{2^{\frac{2}{3}}}=2^{\frac{23}{15}}={\left(a^2\right)}^{\frac{23}{15}}=a^{\frac{46}{15}}$

Vậy $B=a^{\frac{46}{15}}.$

Bài 16 trang 57 Toán 11 Tập 2: Cho x, y là các số thực dương. Rút gọn biểu thức sau:

$A=\frac{x^{\frac{5}{4}}\cdot y+x\cdot y^{\frac{5}{4}}}{\sqrt[4]{x}+\sqrt[4]{y}};$ $B={\left(\sqrt[7]{\frac{x}{y}\sqrt[5]{\frac{y}{x}}}\right)}^{\frac{35}{4}}.$

Lời giải:

Ta có:

$$\begin{gathered} A=\frac{x^{\frac{5}{4}}\cdot y+x\cdot y^{\frac{5}{4}}}{\sqrt[4]{x}+\sqrt[4]{y}}=\frac{x^{\frac{1}{4}}\cdot x\cdot y+x\cdot y\cdot y^{\frac{1}{4}}}{x^{\frac{1}{4}}+y^{\frac{1}{4}}} \\ =\frac{xy\left(x^{\frac{1}{4}}+y^{\frac{1}{4}}\right)}{x^{\frac{1}{4}}+y^{\frac{1}{4}}}=xy; \end{gathered}$$

Bài 17 trang 57 Toán 11 Tập 2: Tìm tập xác định của mỗi hàm số sau:

a) $y=\frac{5}{2^x-3};$ b) $y=\sqrt{25-5^x};$

c) $y=\frac{x}{1-\ln x};$ d) $y=\sqrt{1-{\log }_{3}x}.$

Lời giải:

a) Hàm số $y=\frac{5}{2^x-3}$ xác định ⇔ 2^x – 3 ≠ 0 ⇔2^x ≠ 3 ⇔ x ≠ log₂3.

Vậy tập xác định của hàm số $y=\frac{5}{2^x-3}$là D = ℝ \ {log₂3}.

b) Hàm số $y=\sqrt{25-5^x}$ xác định ⇔ 25 – 5^x ≥ 0 ⇔5^x ≤ 25 ⇔5^x ≤ 5² ⇔ x ≤ 2

Vậy tập xác định của hàm số $y=\sqrt{25-5^x}$là D = (–∞; 2].

c) Hàm số $y=\frac{x}{1-\ln x}$ xác định 

Vậy tập xác định của hàm số $y=\frac{x}{1-\ln x}$là D = (0; +∞) \ {e}.

d) Hàm số $y=\sqrt{1-{\log }_{3}x}$ xác định 

Vậy tập xác định của hàm số $y=\sqrt{1-{\log }_{3}x}$là D = (0; 3].

Giải Toán 11 trang 58 Tập 2

Bài 18 trang 58 Toán 11 Tập 2: Cho a > 0, a ≠ 1 và $a^{\frac{3}{5}}=b.$

a) Viết $a^6;a^{3}b;\frac{a^9}{b^9}$ theo lũy thừa cơ số b.

b) Tính: ${\log }_{a}b;{\log }_a\left(a^2{b}^5\right);{\log }_{\sqrt[5]{a}}\left(\frac{a}{b}\right).$

Lời giải:

a) Ta có:

⦁ ${\text{a}}^6={\left(a^{\frac{3}{5}}\right)}^{10}=b^{10};$

⦁ ${\text{a}}^{3}b={\left(a^{\frac{3}{5}}\right)}^5\cdot b=b^5\cdot b=b^6;$

⦁ $\frac{a^9}{b^9}=\frac{{\left(a^{\frac{3}{5}}\right)}^{15}}{b^9}=\frac{b^{15}}{b^9}=b^6.$

b) Ta có:

⦁ $b=a^{\frac{3}{5}}\Rightarrow {\log }_{a}b={\log }_a{a}^{\frac{3}{5}}=\frac{3}{5};$

⦁ ${\log }_a\left(a^2{b}^5\right)={\log }_a{a}^2+{\log }_a{b}^5$$=2{\log }_{a}a+5{\log }_{a}b=2+5\cdot \frac{3}{5}=2+3=5;$

⦁ ${\log }_{\sqrt[5]{a}}\left(\frac{a}{b}\right)={\log }_{\sqrt[5]{a}}a-{\log }_{\sqrt[5]{a}}b$$=5{\log }_{a}a-5{\log }_{a}b=5-5\cdot \frac{3}{5}=5-3=2.$

Bài 19 trang 58 Toán 11 Tập 2: Giải mỗi phương trình sau:

a) $3^{x^2-4x+5}=9;$ b) 0,5^2x–4 = 4;

c) log₃(2x – 1) = 3; d) logx + log(x – 3) = 1.

Lời giải:

a) $3^{x^2-4x+5}=9\iff 3^{x^2-4x+5}=3^2$$\iff x^2-4\text{x}+5=2\iff x^2-4\text{x}+3=0$

Vậy phương trình có nghiệm là x ∈ {1; 3}.

b) 0,5^2x–4 = 4 ⇔ 2x – 4 = log_0,54

$\iff 2x–4=lo{g}_{2^{-1}}{2}^2\iff 2x–4=-2lo{g}_{2}2$

⇔ 2x – 4 = –2 ⇔ 2x = 2 ⇔ x = 1.

Vậy phương trình có nghiệm là x = 1.

c) log₃(2x – 1) = 3

⇔ 2x – 1 = 3³ ⇔ 2x – 1 = 27

⇔ 2x = 28 ⇔ x = 14.

Vậy phương trình có nghiệm là x = 14.

d) logx + log(x – 3) = 1

Điều kiện xác định là 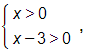 tức là x > 3. Ta có:

logx + log(x – 3) = 1

Vậy phương trình có nghiệm là x = 5.

Bài 20 trang 58 Toán 11 Tập 2: Giải mỗi bất phương trình sau:

a)5^x < 0,125; b) ${\left(\frac{1}{3}\right)}^{2x+1}\ge 3;$

c) log_0,3x > 0; d) ln(x + 4) > ln(2x – 3).

Lời giải:

a) 5^x < 0,125⇔ x < log₅0,125

Vậy bất phương trình có tập nghiệm là (−∞; log₅0,125).

b) ${\left(\frac{1}{3}\right)}^{2x+1}\ge 3$

⇔ 2x + 1 ≤ –1

⇔ 2x ≤ –2

⇔ x ≤ –1

Vậy bất phương trình có tập nghiệm là (–∞; –1].

c) log_0,3x > 0⇔0 < x < 0,3⁰ ⇔0 < x < 1

Vậy bất phương trình có tập nghiệm là (0; 1).

d) ln(x + 4) > ln(2x – 3)

Vậy bất phương trình có tập nghiệm là $\left(\frac{3}{2};7\right).$

Bài 21 trang 58 Toán 11 Tập 2: Trong một trận động đất, năng lượng giải tỏa E (đơn vị: Jun, kí hiệu J) tại tâm địa chấn ở M độ Richter được xác định xấp xỉ bởi công thức: logE ≈ 11,4 + 1,5M.

(Nguồn: Giải tích 12 Nâng cao, NXBGD Việt Nam, 2021).

a) Tính xấp xỉ năng lượng giải tỏa tại tâm địa chấn ở 5 độ Richter.

b) Năng lượng giải tỏa tại tâm địa chấn ở 8 độ Richter gấp khoảng bao nhiêu lần năng lượng giải tỏa tại tâm địa chấn ở 5 độ Richter?

Lời giải:

a) Thay M = 5 vào công thứclogE ≈ 11,4 + 1,5M, ta cónăng lượng giải tỏa tại tâm địa chấn ở 5 độ Richter là:

logE ≈ 11,4 + 1,5 . 5 =18,9

Suy ra E ≈ 10^18,9 (J)

Vậynăng lượng giải toả tại tâm địa chấn ở 5 độ Richter là E ≈ 10^18,9 J.

b) Thay M = 8 vào công thứclogE ≈ 11,4 + 1,5M, ta cónăng lượng giải tỏa tại tâm địa chấn ở 8 độ Richter là:

logE ≈ 11,4 + 1,5 . 8 =23,4

Suy ra E ≈ 10^23,4 (J)

Do đó năng lượng giải tỏa tại tâm địa chấn ở 8 độ Richter gấp khoảng $\frac{{10}^{\mathrm{23,4}}}{{10}^{\mathrm{18,9}}}\approx 31623$ lần năng lượng giải tỏa tại tâm địa chấn ở 5 độ Richter.

Bài 22 trang 58 Toán 11 Tập 2: Trong cây cối có chất phóng xạ $C_6^{14}.$ Khảo sát một mẫu gỗ cổ, các nhà khoa học đo được độ phóng xạ của nó bằng 86% độ phóng xạ của mẫu gỗ tươi cùng loại. Xác định độ tuổi của mẫu gỗ cổ đó. Biết chu kì bán rã của $C_6^{14}$ là T = 5 739 năm, độ phóng xạ của chất phóng xạ tại thời điểm t được cho bởi công thức H = H₀e^–λt với H₀ là độ phóng xạ ban đầu (tại thời điểm t = 0); $\lambda =\frac{\ln 2}{T}$ là hằng số phóng xạ (Nguồn: Vật lí 12, NXBGD Việt Nam, 2021).

Lời giải:

Do độ phóng xạ của $C_6^{14}$ bằng 86% độ phóng xạ của mẫu gỗ tươi cùng loại nên ta có:

H = 86%H₀

⇔ H₀e^–λt = 0,86H₀

⇔ e^–λt = 0,86

⇔ –λt = ln0,86

$\iff t=\frac{\ln \mathrm{0,86}}{-\lambda }$

Mà hằng số phóng xạ là: $\lambda =\frac{\ln 2}{T}=\frac{\ln 2}{5730}$

Do đó $t=\frac{\ln \mathrm{0,86}}{-\frac{\ln 2}{5730}}=-\frac{5730\cdot \ln \mathrm{0,86}}{\ln 2}\approx 1247$ (năm)

Vậy độ tuổi của mẫu gỗ cổ đó là khoảng 1 247 năm.

Xem thêm Lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác: