Toptailieu biên soạn và giới thiệu lời Giải Toán 11 Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi sgk Toán 11 Bài 1 từ đó học tốt môn Toán 11.
Nội dung bài viết
Giải Toán 11 Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác
Hoạt động 1 trang 5 Toán 11 Tập 1: Nêu định nghĩa góc trong hình học phẳng.
Lời giải:
Góc là hình gồm hai tia chung gốc. Mỗi góc có một số đo, đơn vị đo góc là độ hoặc radian.
Số đo của mỗi góc không vượt quá 180∘

Lời giải:
Ta có bảng chuyển đổi số đo độ và số đo radian của một số góc sau:
|
Độ |
18∘ |
2π9.180π=40∘ |
72∘ |
5π6.180π=150∘ |
|
Radian |
18.π180=π10 |
2π9 |
72.π180=2π5 |
5π6 |
Hoạt động 2 trang 6 Toán 11 Tập 1: So sánh chiều quay của kim đồng hồ với:
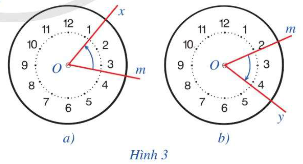
a) Chiều quay từ tia Om đến tia Ox trong Hình 3a.
b) Chiều quay từ tia Om đến tia Oy trong Hình 3b.
Lời giải:
a) Chiều quay từ tia Om đến tia Ox trong Hình 3a là chiều quay ngược chiều kim đồng hồ
b) Chiều quay từ tia Om đến tia Oy trong Hình 3b là chiều quay cùng chiều kim đồng hồ.
Lời giải:
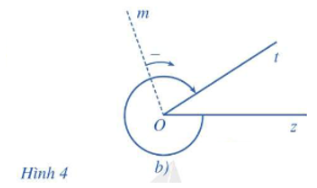
Trong Hình 4b, góc lượng giác là (Oz,Ot) với tia đầu là tia Oz và tia cuối là tia Ot
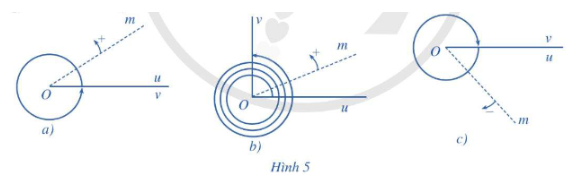
b) Trong Hình 5b, tia Om quay theo chiều dương ba vòng và một phần tư vòng ( tức là 314vòng). Hỏi tia đó quét nên một góc bao nhiêu độ?
c) Trong Hình 5x, toa Om quay theo chiều âm đúng một vòng. Hỏi tia đó quét nên một góc bao nhiêu độ?
Lời giải:
a) Trong Hình 5a, tia Om quay theo chiều dương đúng một vòng. Tia đó quét nên một góc 360∘
b) Trong Hình 5b, tia Om quay theo chiều dương ba vòng và một phần tư vòng ( tức là 314vòng). Tia đó quét nên một góc 3.360∘+14360∘=1170∘
c) Trong Hình 5x, toa Om quay theo chiều âm đúng một vòng. Tia đó quét nên một góc -360∘
Lời giải:
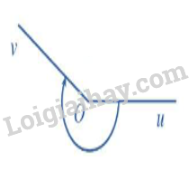
Ta có −5π4=−π+(−π4). Góc lượng giác gốc O có tia đầu Ou, tia cuối Ov và có số đo −5π4 được biểu diễn ở hình sau:
Lời giải:
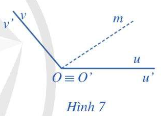
Quan sát Hình 7 ta thấy:
• Tia Om quay (chỉ theo chiều dương) xuất phát từ tia Ou đến trùng với tia Ov rồi quay tiếp một số vòng đến trùng với tia cuối Ov;
• Tia Om quay (chỉ theo chiều dương) xuất phát từ tia O′u′≡Ou đến trùng với tia O′v′≡Ovrồi quay tiếp một số vòng đến trùng với tỉa cuối O′v′≡Ov.
Như vậy, sự khác biệt giữa hai góc lượng giác (Ou, Ov) và (O’u’, O’v’) chính là số vòng quay quanh điểm O. Vì vậy, sự khác biệt giữa số đo của hai góc lượng giác đó chính là bội nguyên của 360∘ khi hai góc đó tính theo đơn vị độ (hay bội nguyên của 2π rad khi hai góc đó tính theo đơn vị radian).
Lời giải:
Ta có:
(O′u′,O′v′)=(Ou,Ov)+k2π=−4π3+k2π(k∈Z)
Lời giải:
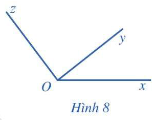
Ta có : ^xOz=^xOy+^yOz
Lời giải:
Theo hệ thức Chasles, ta có:
(Ov,Ow)=(Ou,Ov)−(Ou,Ow)+k2π=−11π4−3π4+k2π=−72+k2π,(k∈Z)
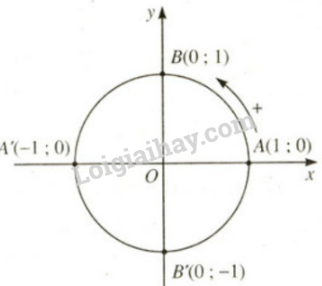
b) Hãy nêu chiều dương, chiều âm trên đường tròn tâm O với bán kính bằng 1
Lời giải:
a) b)
b) So sánh hoành độ của điểm M với cos60∘; tung độ của điểm M với sin60∘
Lời giải:
a)
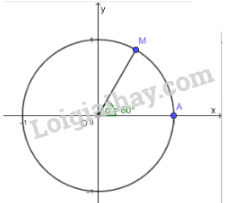
b) cos60∘ bằng hoành độ của điểm M
sin60∘ bằng tung độ của điểm M
Luyện tập - Vận dụng 7 trang 11 Toán 11 Tập 1: Tìm giác trị lượng giác của góc lượng giác β=−π4
Lời giải:
sin(−π4)=−√22;cos(−π4)=√22;tan(−π4)=−12;cot(−π4)=−2
Hoạt động 8 trang 11 Toán 11 Tập 1: Xét dấu các giá trị lượng giác của góc lượng giác α=−30∘
Lời giải:
cos(−30∘)=√32>0sin(−30∘)=−12<0tan(−30∘)=−√33<0cot(−30∘)=−√3<0
Lời giải:
Do π2<5π6<π nên
cos(5π6)<0sin(5π6)>0tan(5π6)<0cot(5π6)<0
Hoạt động 9 trang 11 Toán 11 Tập 1: Cho góc lượng giác α. So sánh
a) cos2α+sin2α và 1
b) tanα.cotα và 1 với cosα≠0;sinα≠0
c) 1+tan2α và 1cos2α với cosα≠0
d) 1+cot2α và 1sin2α với sinα≠0
Lời giải:
a) cos2α+sin2α=1
b) tanα.cotα=sinαcosα.cosαsinα=1
c) sin2α+cos2αcos2α=sin2αcos2α+cos2αcos2α=tan2α+1
d) 1sin2α=sin2α+cos2αsin2α=sin2αsin2α+cos2αsin2α=1+cot2α
Lời giải:
Vì cos2α+sin2α=1 nên cos2α=1−sin2α=1−(−45)2=925
Do π<α<3π2 nên cosα<0. Suy ra cosα=−35
Hoạt động 10 trang 12 Toán 11 Tập 1: Tìm các giá trị lượng giác của góc lượng giác α=45∘
Lời giải:
sin(45∘)=√22;cos(45∘)=√22;tan(45∘)=12;cot(45∘)=2
Luyện tập - Vận dụng 10 trang 12 Toán 11 Tập 1: Tính giá trị của biểu thức:
Q=tan2π3+sin2π4+cotπ4+cosπ2
Lời giải:
Ta có:
Q=tan2π3+sin2π4+cotπ4+cosπ2=(√3)2+(√22)2+1+0=72
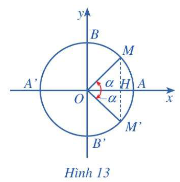 a) Đối với hai điểm M, M’ nêu nhận xét về: hoành độ của chúng, tung độ của chúng.
a) Đối với hai điểm M, M’ nêu nhận xét về: hoành độ của chúng, tung độ của chúng.
b) Nêu mối liên hệ giữa các giá trị lượng giác tương ứng của hai góc lượng giác αv\'a−α
Lời giải:
a) Hoành độ của điểm M và M’ bằng nhau
Tung độ của điểm M và M’ đối nhau
b) Mối liên hệ giữa các giá trị lượng giác tương ứng của hai góc lượng giác αv\'a−α

Luyện tập - Vận dụng 11 trang 14 Toán 8 Tập 1: a) cos2π8+cos23π8
b) tan1∘.tan2∘.tan45∘.tan88∘.tan89∘
Lời giải:
a) cos2π8+cos23π8=cos2π8+cos2(π2−π8)=cos2π8+sin2π8=1
b)
tan1∘.tan2∘.tan45∘.tan88∘.tan89∘=(tan1∘.tan89∘).(tan2∘.tan88∘).tan45∘=(tan1∘.cot1∘).(tan2∘.cot2∘).tan45∘=1
Luyện tập - Vận dụng 12 trang 14 Toán 11 Tập 1: Dùng máy tính cầm tay để tính ;
a) tan(−75∘);b) cot(−π5)
Lời giải:
a) tan(−75∘)=−2−√3
b) cot(−π5)≈−1,376
Lời giải:
Hình minh họa:
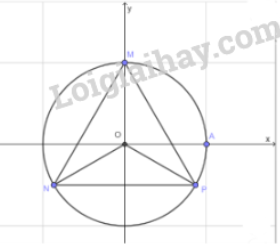
Lời giải:
cos(225∘)=cos(180∘+45∘)=−cos(45∘)=−√22sin(225∘)=sin(180∘+45∘)=−sin(45∘)=−√22tan(225∘)=sin(225∘)cos(225∘)=1cot(225∘)=1tan(225∘)=1
cos(−225∘)=cos(225∘)=cos(180∘+45∘)=−cos(45∘)=−√22sin(−225∘)=−sin(225∘)=−sin(180∘+45∘)=sin(45∘)=√22tan(−225∘)=sin(225∘)cos(225∘)=−1cot(−225∘)=1tan(225∘)=−1
cos(−1035∘)=cos(1035∘)=cos(6.360∘−45∘)=cos(−45∘)=cos(45∘)=√22sin(−1035∘)=−sin(1035∘)=−sin(6.360∘−45∘)=−sin(−45∘)=sin(45∘)=√22tan(−1035∘)=sin(−1035∘)cos(−1035∘)=1cot(−1035∘)=1tan(−1035∘)=−1
cos(5π3)=cos(π+2π3)=−cos(2π3)=12sin(5π3)=sin(π+2π3)=−sin(2π3)=−√32tan(5π3)=sin(5π3)cos(5π3)=−√3cot(5π3)=1tan(5π3)=−√33
cos(19π2)=cos(8π+3π2)=cos(3π2)=cos(π+π2)=−cos(π2)=0sin(19π2)=sin(8π+3π2)=sin(3π2)=sin(π+π2)=−sin(π2)=−1tan(19π2)cot(19π2)=cos(19π2)sin(19π2)=0
cos(−159π4)=cos(159π4)=cos(40.π−π4)==cos(−π4)=cos(π4)=√22sin(−159π4)=−sin(159π4)=−sin(40.π−π4)=−sin(−π4)=sin(π4)=√22tan(−159π4)=cos(−159π4)sin(−159π4)=1cot(−159π4)=1tan(−159π4)=1
Bài 3 trang 15 Toán 11 Tập 1: Tính các giá trị lượng giác (nếu có) có mỗi góc sau:
a) π3+k2π(k∈Z)
b) kπ(k∈Z)
c) π2+kπ(k∈Z)
d) π4+kπ(k∈Z)
Lời giải:
a)
cos(π3+k2π)=cos(π3)=12sin(π3+k2π)=sin(π3)=√32tan(π3+k2π)=sin(π3+k2π)cos(π3+k2π)=√3cot(π3+k2π)=1tan(π3+k2π)=√33
b)
cos(kπ)=[−1;k=2n+11;k=2nsin(kπ)=0tan(kπ)=sin(kπ)cos(kπ)=0cot(kπ)
c)
cos(π2+kπ)=0sin(π2+kπ)=[sin(−π2)=−1;k=2n+1sin(π2)=1;k=2ntan(π2+kπ)cot(π2+kπ)=0
d)
Với k=2n+1 thì
Với k=2n thì
Bài 4 trang 15 Toán 11 Tập 1: Tính các giá trị lượng giác của góc trong mỗi trường hợp sau:
a) với
b) với
c) với
d) với
Lời giải:
a) Ta có
mà nên
Lại có nên
Khi đó
b)
Ta có
mà nên
Lại có nên
Khi đó
c)
Ta có nên
Mà
Với thì
Với thì
và thì
d)
Ta có nên
Mà
Với thì
Với thì
và thì
Bài 5 trang 15 Toán 11 Tập 1: Tính
a) (17 số hạng)
b) (35 số hạng)
Lời giải:
a)
b)
a) Hãy tính quãng đường vệ tinh đã chuyển độ được sau: 1h; 3h; 5h
b) Vệ tinh chuyển động được quãng đường 200 000 km sau bao nhiêu giờ (làm tròn kết quả đến hàng đơn vị?
Lời giải:
a) Chiều dài một vòng của quỹ đạo là : (km)
Quãng đường vệ tinh đã chuyển độ được sau 1 giờ là
(km)
Quãng đường vệ tinh đã chuyển độ được sau 3 giờ là (km)
Quãng đường vệ tinh đã chuyển độ được sau 1 giờ là
(km)
b)Vệ tinh chuyển động được quãng đường 200 000 km sau sô giờ là : ( giờ)
Xem thêm các bài giải sách giáo khoa Toán 11 Cánh Dều hay, chi tiết khác:
Bài 2: Các phép biến đổi lượng giác
Bài 3: Hàm số lượng giác và đồ thị
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.