Toptailieu biên soạn và giới thiệu lời giải Toán 11 (Cánh diều) Bài tập cuối chương 1 trang 41 hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi SGK Toán 11 Bài tập cuối chương 1 trang 41 từ đó học tốt môn Toán 11.

Giải Bài tập cuối chương 1 trang 41 SGK Toán 11 Tập 1 (Cánh Diều)

Giải Toán 11 trang 41 Tập 1

Bài 1 trang 41 Toán 11 Tập 1: Hàm số y = sinx đồng biến trên khoảng:

A. (0; π).

B. $\left(-\frac{3\pi }{2};-\frac{\pi }{2}\right)$ .

C. $\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$

D. (‒π; 0).

Lời giải:

Đáp án đúng là: C

Cách 1. Dựa vào đồ thị hàm số:

Đồ thị hàm số y = sinx (hình vẽ):

Quan sát đồ thị trên, ta thấy hàm số y = sinx đồng biến trên khoảng $\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ .

Cách 2. Dùng tính chất của hàm số y = sinx:

Hàm số y = sinx đồng biến trên mỗi khoảng $\left(-\frac{\pi }{2}+k2\pi ;\frac{\pi }{2}+k2\pi \right)$ với k ∈ ℤ.

Do đó hàm số y = sinx đồng biến trên khoảng $\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ .

Bài 2 trang 41 Toán 11 Tập 1: Hàm số nghịch biến trên khoảng (π; 2π) là:

A. y = sinx.

B. y = cosx.

C. y = tanx.

D. y = cotx.

Lời giải:

Đáp án đúng là: D

Cách 1. Dùng đồ thị hàm số:

Xét đồ thị hàm số y = sinx:

Xét đồ thị hàm số y = cosx:

Xét đồ thị hàm số y = tanx:

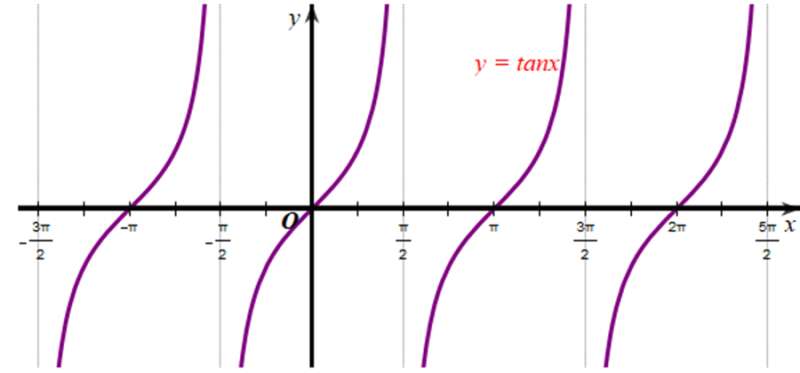
Xét đồ thị hàm số y = cotx:

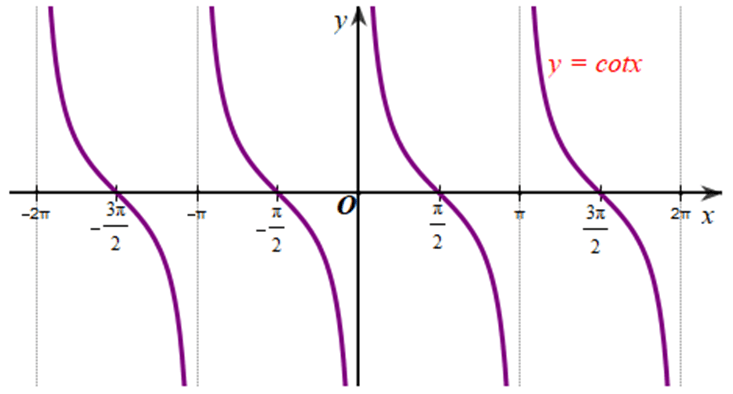
Quan sát các đồ thị trên, ta thấy hàm số y = cotx nghịch biến trên khoảng (π; 2π).

Cách 2. Dùng tính chất của hàm số lượng giác:

Do (π; 2π) = (0 + π; π + π)

Mà hàm số y = cotx nghịch biến trên mỗi khoảng (kπ; π + kπ) với k ∈ ℤ.

Do đó hàm số y = cotx nghịch biến trên khoảng (π; 2π).

Bài 3 trang 41 Toán 11 Tập 1: Nếu tan(a + b) = 3, tan(a – b) = ‒3 thì tan2a bằng:

A. 0.

B. $\frac{3}{5}$ .

C. 1.

D. -$\frac{3}{4}$.

Lời giải:

Đáp án đúng là: A

Ta có:

tan2a = tan[(a + b) + (a – b)]

$=\frac{\tan \left(a+b\right)+\tan \left(a-b\right)}{1-\tan \left(a+b\right)\tan \left(a-b\right)}=\frac{3+\left(-3\right)}{1-3.\left(-3\right)}=0$.

Bài 4 trang 41 Toán 11 Tập 1: Nếu cosa = $\frac{1}{4}$ thì cos2a bằng:

A. $\frac{7}{8}$ .

B. -$\frac{7}{8}$.

C. $\frac{15}{16}$ .

D. -$\frac{15}{16}$.

Lời giải:

Đáp án đúng là: B

Ta có: cos2a = 2cos²a – 1 = $2.{\left(\frac{1}{4}\right)}^2-1=2.\frac{1}{16}-1=-\frac{7}{8}$.

Bài 5 trang 41 Toán 11 Tập 1: Nếu cosa = $\frac{3}{5}$ và cosb = $-\frac{4}{5}$ thì cos(a + b)cos(a – b) bằng:

A. 0.

B. 2.

C. 4.

D. 5.

Lời giải:

Đáp án đúng là: A

Áp dụng công thức biến đổi tích thành tổng, ta có:

cos (a+b)cos(a-b) = $\frac{1}{2}$[cos(a+b+a-b) + cos(a+b-a+b)]

= $\frac{1}{2}$[cos2a + cos2b]

Ta lại có:

cos2a = 2cos²a – 1 = $2.{\left(\frac{3}{5}\right)}^2-1=2.\frac{9}{25}-1=-\frac{7}{25}$;

cos2b = 2cos²b – 1 = $2.{\left(-\frac{4}{5}\right)}^2-1=2.\frac{16}{25}-1=\frac{7}{25}$;

Do đó cos(a+b)cos(a-b) = $\frac{1}{2}$[cos2a + cos2b] = $\frac{1}{2}$.$\left(-\frac{7}{25}+\frac{7}{25}\right)$=0.

Bài 6 trang 41 Toán 11 Tập 1: Nếu sina = $-\frac{\sqrt{2}}{3}$ thì sin$\left(a+\frac{\pi }{4}\right)+\sin \left(a-\frac{\pi }{4}\right)$ bằng:

A. $\frac{2}{3}$ .

B. $\frac{1}{3}$ .

C. -$\frac{2}{3}$.

D. -$\frac{1}{3}$.

Lời giải:

Đáp án đúng là: C

Áp dụng công thức biến đổi tổng thành tích, ta có:

sin$\left(a+\frac{\pi }{4}\right)+\sin \left(a-\frac{\pi }{4}\right)$

= 2sin$\left(\frac{a+\frac{\pi }{4}+a-\frac{\pi }{4}}{2}\right)\cos \left(\frac{a+\frac{\pi }{4}-a+\frac{\pi }{4}}{2}\right)$

= 2sinacos$\frac{\pi }{4}=2.\left(-\frac{\sqrt{2}}{3}\right).\frac{\sqrt{2}}{2}=-\frac{2}{3}$.

Bài 7 trang 41 Toán 11 Tập 1: Số nghiệm của phương trình cosx = 0 trên đoạn [0; 10π] là:

A. 5.

B. 9.

C. 10.

D. 11.

Lời giải:

Đáp án đúng là: C

Cách 1. Giải phương trình lượng giác

cosx = 0

$\iff$x = $\frac{\pi }{2}$+k$\pi$ (k ∈ ℤ)

Do x ∈ [0; 10π] nên ta có: 0$\le$$\frac{\pi }{2}$+k$\pi$$\le$10$\pi$

$\iff$0$\le$$\frac{\pi }{2}$+k$\le$10 $\iff$ -$\frac{1}{2}$$\le$k$\le$$\frac{19}{2}$

Mà k ∈ ℤ nên k ∈ {0; 1; 2; …; 9}, khi đó ta tìm được 10 giá trị của x.

Vậy phương trình cosx = 0 có 10 nghiệm trên đoạn [0; 10π].

Cách 2. Dùng đồ thị hàm số

Quan sát đồ thị ta thấy đồ thị hàm số y = cosx cắt trục hoành tại 10 điểm A, B, C, …, K trên đoạn [0; 10π].

Vậy phương trình cosx = 0 có 10 nghiệm trên đoạn [0; 10π].

Bài 8 trang 41 Toán 11 Tập 1: Số nghiệm của phương trình sinx = 0 trên đoạn [0; 10π] là:

A. 10.

B. 6.

C. 5.

D. 11.

Lời giải:

Đáp án đúng là: D

Cách 1. Giải phương trình lượng giác

sinx = 0

$\iff$ x = kπ (k ∈ ℤ)

Do x ∈ [0; 10π] nên ta có: 0 ≤ kπ ≤ 10π

$\iff$ 0 ≤ k ≤ 10

Mà k ∈ ℤ nên k ∈ {0; 1; 2; …; 10}, khi đó ta tìm được 11 giá trị của x.

Vậy phương trình sinx = 0 có 11 nghiệm trên đoạn [0; 10π].

Cách 2. Dùng đồ thị hàm số

Quan sát đồ thị ta thấy đồ thị hàm số y = sinx cắt trục hoành tại 11 điểm A ≡ O, B, C, …, M trên đoạn [0; 10π].

Vậy phương trình sinx = 0 có 11 nghiệm trên đoạn [0; 10π].

Bài 9 trang 41 Toán 11 Tập 1: Phương trình cotx = ‒1 có nghiệm là:

A. $-\frac{\pi }{4}+k\pi \left(k\in \mathbb{Z}\right)$ .

B. $\frac{\pi }{4}+k\pi \left(k\in \mathbb{Z}\right)$ .

C. $\frac{\pi }{4}+k2\pi \left(k\in \mathbb{Z}\right)$ .

D. -$\frac{\pi }{4}+k2\pi \left(k\in \mathbb{Z}\right)$.

Lời giải:

Đáp án đúng là: A

Ta có: cotx = ‒1

$\iff x=-\frac{\pi }{4}+k\pi \left(k\in \mathbb{Z}\right)$.

Bài 10 trang 41 Toán 11 Tập 1: Số nghiệm của phương trình sin$\left(x+\frac{\pi }{4}\right)=\frac{\sqrt{2}}{2}$ trên đoạn [0; π] là:

A. 4.

B. 1.

C. 2.

D. 3.

Lời giải:

Đáp án đúng là: C

Cách 1. Giải phương trình lượng giác:

Ta có:

$\sin \left(x+\frac{\pi }{4}\right)=\frac{\sqrt{2}}{2}$

$\iff \sin \left(x+\frac{\pi }{4}\right)=\sin \frac{\pi }{4}$

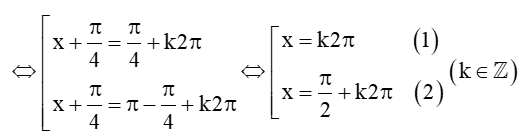
• Do x ∈ [0; π] nên từ (1) ta có:

0 ≤ k2π ≤ π

$\iff$ 0 ≤ 2k ≤ 1

$\iff$ 0 ≤ k ≤ $\frac{1}{2}$

Mà k ∈ ℤ nên k = 0, khi đó ta tìm được 1 giá trị của x (x = 0) trong trường hợp này.

• Do x ∈ [0; π] nên từ (2) ta có:

0 ≤ $\frac{\pi }{2}$+k2$\pi$ ≤ $\pi$

$\iff$ 0 ≤ $\frac{1}{2}$+2k ≤ 1

$\iff -\frac{1}{2}\le 2k\le \frac{1}{2}\iff -\frac{1}{4}\le k\le \frac{1}{4}$

Mà k ∈ ℤ nên k = 0, khi đó ta tìm được 1 giá trị của x $\left(x=\frac{\pi }{2}\right)$ trong trường hợp này.

Vậy phương trình sin$\left(x+\frac{\pi }{4}\right)=\frac{\sqrt{2}}{2}$ có hai nghiệm trên đoạn [0; π].

Cách 2. Dùng đồ thị hàm số

Đặt x+$\frac{\pi }{4}=\alpha$. Khi đó ta có phương trình sin$\alpha =\frac{\sqrt{2}}{2}$.

Xét đường thẳng y = $\frac{\sqrt{2}}{2}$ và đồ thị hàm số y = sinα trên đoạn [0; π]:

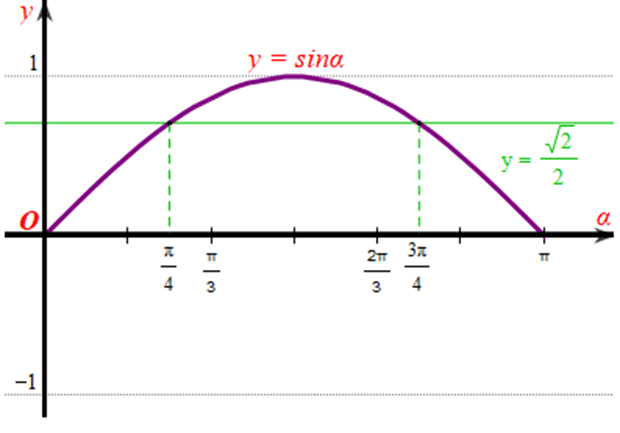
Từ đồ thị hàm số trên ta thấy đường thẳng y = $\frac{\sqrt{2}}{2}$ cắt đồ thị số y = sinα trên đoạn [0; π] tại hai điểm có hoành độ lần lượt là ${\alpha }_1=\frac{\pi }{4}$ và ${\alpha }_2=\frac{3\pi }{4}$.

Mà x+$\frac{\pi }{4}=\alpha$ , khi đó ta sẽ tìm được 2 giá trị x là x₁ = 0 và $x_2=\frac{\pi }{2}$.

Vậy phương trình sin$\left(x+\frac{\pi }{4}\right)=\frac{\sqrt{2}}{2}$ có hai nghiệm trên đoạn [0; π].

Xem thêm các bài giải sách giáo khoa Toán 11 Cánh Dều hay, chi tiết khác:

Bài 3: Hàm số lượng giác và đồ thị

Bài 4: Phương trình lượng giác cơ bản

Bài 1: Dãy số

Bài 2: Cấp số cộng

Bài 3: Cấp số nhân