Toptailieu.vn xin giới thiệu Lý thuyết Các phép biến đổi lượng giác (Cánh diều) hay, chi tiết | Lý thuyết Toán 11 Bài viết gồm phần lý thuyết trọng tâm nhất được trình bày một cách dễ hiểu, dễ nhớ bên cạnh đó là bộ câu hỏi trắc nghiệm có hướng dẫn giải chi tiết để học sinh có thể vận dụng ngay lý thuyết, nắm bài một cách hiệu quả nhất. Mời các bạn đón xem:
Lý thuyết Các phép biến đổi lượng giác (Cánh diều) hay, chi tiết | Lý thuyết Toán 11
Bài giải Bài 2: Các phép biến đổi lượng giác
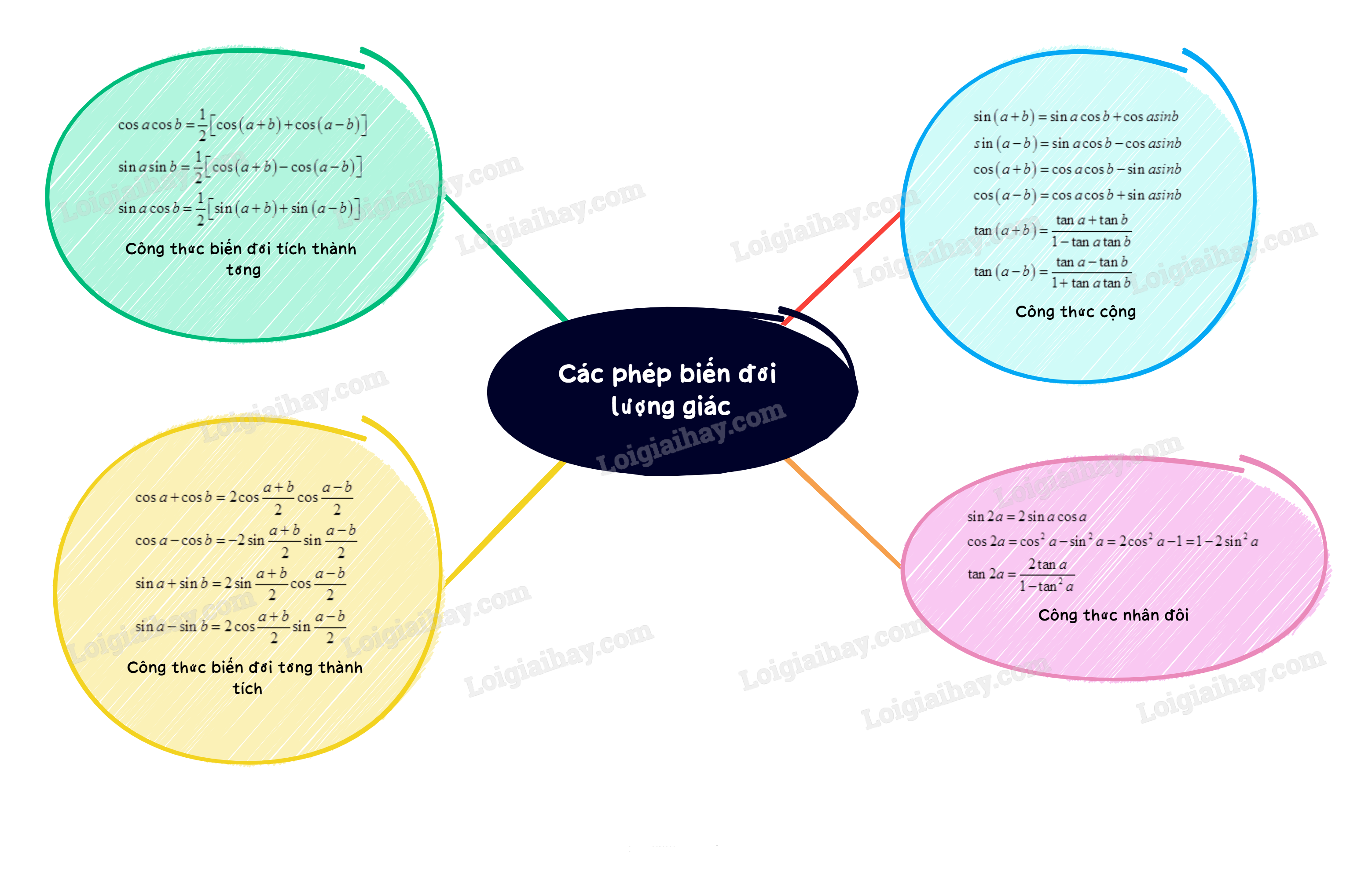
A. Lý thuyết Các phép biến đổi lượng giác
I. Công thức cộng
II. Công thức nhân đôi
Suy ra, công thức hạ bậc:
III. Công thức biến đổi tích thành tổng
IV. Công thức biến đổi tổng thành tích
B. Bài tập Các phép biến đổi lượng giác
Bài 1. Cho ∆ABC. Chứng minh rằng:
a) ;
b) ;
c) , với R là bán kính đường tròn ngoại tiếp ∆ABC và S là diện tích ∆ABC.
Hướng dẫn giải
∆ABC, có: , suy ra
Do đó .
b)
Vậy ta có điều phải chứng minh.
c) VT = sin2A + sin2B + sin2C
= 2sin(A + B).cos(A – B) + 2sinC.cosC
= 2sin(180° – C).cos(A – B) + 2sinC.cosC
= 2sinC.cos(A – B) + 2sinC.cosC
= 2sinC.[cos(A – B) + cosC]
= 2sinC.[cos(A – B) + cos(180° – A – B)]
= 2sinC.[cos(A – B) – cos(A + B)]
= –4sinC.sinA.sin(–B)
= 4sinA.sinB.sinC
.
Vậy ta có điều phải chứng minh.
Bài 2. Chứng minh rằng:
a) ;
Hướng dẫn giải
a) VT = cos3x.sinx – sin3x.cosx
= cosx.sinx.(cos2x – sin2x)
= VP.
Vậy ta có điều phải chứng minh.
Bài 3. Cho , với . Tính sina, cosa, 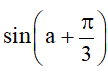
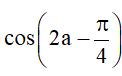
Hướng dẫn giải
Vì nên sina > 0, cosa > 0.
• Áp dụng công thức hạ bậc, ta được:
Suy ra (do sina > 0)
• Áp dụng công thức hạ bậc, ta được: .
Suy ra .
• Áp dụng công thức cộng đối với sin, ta được:
.
• Áp dụng công thức nhân đôi, ta được:
.
• Áp dụng công thức cộng đối với côsin, ta được:
Bài 4. Tính α + β biết .
Hướng dẫn giải
Áp dụng công thức cộng đối với tang, ta được:
Vậy .
Xem thêm Lý thuyết các bài Toán 11 Cánh diều hay, chi tiết khác:
Lý thuyết Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác
Lý thuyết Bài 3: Hàm số lượng giác và đồ thị
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.