SBT Toán 11 (Cánh diều) Bài 2: Các phép biến đổi lượng giác

Ngọc Nguyễn Ngày: 15-03-2024 Lớp 11

277

Toptailieu biên soạn và giới thiệu giải Sách bài tập Toán 11 Bài 2: Các phép biến đổi lượng giác sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 11 Bài 2.

SBT Toán 11 (Cánh diều) Bài 2: Các phép biến đổi lượng giác

SBT Toán 11 trang 14 Tập 1 (Cánh Diều)

Bài 15 trang 14 SBT Toán 11 Tập 1: Cho hai góc a và b với tan a = $\frac{1}{7}$ và tanb = $\frac{3}{4} .$ Khi đó, tan(a + b) bằng:

A. 1.

B. $- \frac{17}{31}$ .

C. $\frac{17}{31}$ .

D. – 1.

Lời giải:

Đáp án đúng là: A

Ta có $\tan (a + b) = \frac{\tan a + \tan b}{1 - \tan a . \tan b} = \frac{\frac{1}{7} + \frac{3}{4}}{1 - \frac{1}{7} . \frac{3}{4}} = \frac{\frac{25}{28}}{\frac{25}{28}} = 1$ .

Bài 16 trang 14 SBT Toán 11 Tập 1: Nếu $\sin α = \frac{1}{\sqrt{3}}$ với $0 < α < \frac{π}{2}$ thì giá trị của $\cos (α + \frac{π}{3})$ bằng:

A. $\frac{\sqrt{6}}{6} - \frac{1}{2}$ .

B. $\sqrt{6} - 3$ .

C. $\frac{\sqrt{6}}{6} - 3$ .

D. $\sqrt{6} - \frac{1}{2}$ .

Lời giải:

Đáp án đúng là: A

Vì $0 < α < \frac{π}{2}$ nên cos α > 0, do đó từ sin² α + cos² α = 1, suy ra

$\cos α = \sqrt{1 - \sin^{2} α} = \sqrt{1 - {(\frac{1}{\sqrt{3}})}^{2}} = \frac{\sqrt{6}}{3}$ .

Ta có $\cos (α + \frac{π}{3})$ $= \cos α \cos \frac{π}{3} - \sin α \sin \frac{π}{3}$ $= \frac{\sqrt{6}}{3} . \frac{1}{2} - \frac{1}{\sqrt{3}} . \frac{\sqrt{3}}{2} = \frac{\sqrt{6}}{6} - \frac{1}{2}$ .

Bài 17 trang 14 SBT Toán 11 Tập 1: Nếu $\sin α = \frac{2}{3}$ thì giá trị của biểu thức $P = (1 - 3 \cos 2 α) (2 + 3 \cos 2 α)$ bằng:

A. $\frac{11}{9}$ .

B. $\frac{12}{9}$ .

C. $\frac{13}{9}$ .

D. $\frac{14}{9}$ .

Lời giải:

Đáp án đúng là: D

Ta có $P = (1 - 3 \cos 2 α) (2 + 3 \cos 2 α)$

Nếu sinα = 2/3 thì giá trị của biểu thức P = (1 - 3cos2α)(2 + 3cos2α) bằng

SBT Toán 11 trang 15 Tập 1 (Cánh Diều)

Bài 18 trang 15 SBT Toán 11 Tập 1: Chọn đẳng thức đúng trong các đẳng thức sau:

A. $\sin^{4} x + \cos^{4} x = \frac{3 - \cos 4 x}{4}$ .

B. $\sin^{4} x + \cos^{4} x = \frac{3 + \cos 4 x}{4}$ .

C. $\sin^{4} x + \cos^{4} x = \frac{3 + \cos 4 x}{2}$ .

D. $\sin^{4} x + \cos^{4} x = \frac{3 - \cos 4 x}{2}$ .

Lời giải:

Đáp án đúng là: B

Ta có sin⁴ x + cos⁴ x = 1 – 2sin² x cos² x (theo Bài 9a)

= 1 – 2 (sin x cos x)² = $1 - 2 {(\frac{\sin 2 x}{2})}^{2} = 1 - 2. \frac{\sin^{2} 2 x}{4} = 1 - \frac{2 (1 - \cos^{2} 2 x)}{4}$

$= 1 - \frac{2 - 2 \cos^{2} 2 x}{4} = \frac{4 - 2 + 2 \cos^{2} 2 x}{4}$ $= \frac{3 + (2 \cos^{2} 2 x - 1)}{4} = \frac{3 + \cos 4 x}{4}$ .

Vậy $\sin^{4} x + \cos^{4} x = \frac{3 + \cos 4 x}{4}$ .

Bài 19 trang 15 SBT Toán 11 Tập 1: Rút gọn biểu thức cos(120° – x) + cos(120° + x) – cos x ta được kết quả là:

A. – 2cos x.

B. – cos x.

C. 0.

D. sin x – cos x.

Lời giải:

Đáp án đúng là: A

Ta có cos(120° – x) + cos(120° + x) – cos x

= cos 120° cos x + sin 120° sin x + cos 120° cos x – sin 120° sin x – cos x

= 2 cos 120° cos x – cos x

= 2 . $(- \frac{1}{2})$ . cos x – cos x

= – cos x – cos x

= – 2 cos x.

Bài 20 trang 15 SBT Toán 11 Tập 1: Nếu $\cos a = \frac{3}{4}$ thì giá trị của $\cos \frac{a}{2} \cos \frac{a}{2}$ bằng:

A. $\frac{23}{16}$ .

B. $\frac{7}{8}$ .

C. $\frac{7}{16}$ .

D. $\frac{23}{8}$ .

Lời giải:

Đáp án đúng là: B

Ta có $\cos \frac{a}{2} \cos \frac{a}{2} = \cos^{2} \frac{a}{2} = \frac{1 + \cos 2. \frac{a}{2}}{2} = \frac{1 + \cos a}{2} = \frac{1 + \frac{3}{4}}{2} = \frac{7}{8}$ .

Bài 21 trang 15 SBT Toán 11 Tập 1: Nếu $\cos a = \frac{\sqrt{5}}{3}$ thì giá trị của biểu thức $A = 4 \sin (a + \frac{π}{3}) \sin (a - \frac{π}{3})$ bằng:

A. $- \frac{11}{9}$ .

B. $\frac{11}{9}$ .

C. $- \frac{1}{9}$ .

D. $\frac{1}{9}$ .

Lời giải:

Đáp án đúng là: A

Ta có $A = 4 \sin (a + \frac{π}{3}) \sin (a - \frac{π}{3})$

Bài 21 trang 15 SBT Toán 11 Tập 1

$= - 2 (\cos 2 a - \cos \frac{2 π}{3})$

Bài 21 trang 15 SBT Toán 11 Tập 1

Bài 22 trang 15 SBT Toán 11 Tập 1: Nếu $\cos a = \frac{1}{3}, \sin b = \frac{- 2}{3}$ thì giá trị cos(a + b) cos(a − b) bằng:

A. $- \frac{2}{3}$ .

B. $\frac{1}{3}$ .

C. $\frac{2}{3}$ .

D. $- \frac{1}{3}$ .

Lời giải:

Đáp án đúng là: D

Ta có cos(a + b) cos(a − b) Nếu cosa = 1/3, sinb = -2/3 thì giá trị cos(a + b) cos(a − b) bằng

$= \frac{1}{2} (\cos 2 a + \cos 2 b)$

Nếu cosa = 1/3, sinb = -2/3 thì giá trị cos(a + b) cos(a − b) bằng

Bài 23 trang 15 SBT Toán 11 Tập 1: Giá trị của biểu thức $P = \frac{\sin \frac{π}{9} + \sin \frac{5 π}{9}}{\cos \frac{π}{9} + \cos \frac{5 π}{9}}$ bằng:

A. $\frac{1}{\sqrt{3}}$ .

B. $- \frac{1}{\sqrt{3}}$ .

C. $\sqrt{3}$ .

D. $- \sqrt{3}$ .

Lời giải:

Đáp án đúng là: C

Ta có $P = \frac{\sin \frac{π}{9} + \sin \frac{5 π}{9}}{\cos \frac{π}{9} + \cos \frac{5 π}{9}}$ $= \frac{2 \sin \frac{\frac{π}{9} + \frac{5 π}{9}}{2} \cos \frac{\frac{π}{9} - \frac{5 π}{9}}{2}}{2 \cos \frac{\frac{π}{9} + \frac{5 π}{9}}{2} \cos \frac{\frac{π}{9} - \frac{5 π}{9}}{2}}$

$= \frac{\sin \frac{π}{3} \cos (- \frac{2 π}{9})}{\cos \frac{π}{3} \cos (- \frac{2 π}{9})} = \frac{\sin \frac{π}{3}}{\cos \frac{π}{3}} = \frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} = \sqrt{3}$ .

Bài 24 trang 15 SBT Toán 11 Tập 1: Rút gọn biểu thức $A = \frac{\sin x + \sin 2 x + \sin 3 x}{\cos x + \cos 2 x + \cos 3 x}$ ta được kết quả là:

A. tan x.

B. tan 3x.

C. tan 2x.

D. tan x + tan 2x + tan 3x.

Lời giải:

Đáp án đúng là: C

Ta có $A = \frac{\sin x + \sin 2 x + \sin 3 x}{\cos x + \cos 2 x + \cos 3 x}$ $= \frac{(\sin x + \sin 3 x) + \sin 2 x}{(\cos x + \cos 3 x) + \cos 2 x}$

$= \frac{2 \sin \frac{x + 3 x}{2} \cos \frac{x - 3 x}{2} + \sin 2 x}{2 \cos \frac{x + 3 x}{2} \cos \frac{x - 3 x}{2} + \cos 2 x}$ $= \frac{2 \sin 2 x \cos (- x) + \sin 2 x}{2 \cos 2 x \cos (- x) + \cos 2 x}$

$= \frac{\sin 2 x (2 \cos x + 1)}{\cos 2 x (2 \cos x + 1)} = \frac{\sin 2 x}{\cos 2 x} = \tan 2 x$ .

Bài 25 trang 15 SBT Toán 11 Tập 1: Cho $\sin a = \frac{2}{3}$ với $\frac{π}{2} < a < π$ . Tính:

a) cos a, tan a;

b) $\sin (a + \frac{π}{4}), \cos (a - \frac{5 π}{6}), \tan (a + \frac{2 π}{3})$ ;

c) sin 2a, cos 2a.

Lời giải:

a) Vì $\frac{π}{2} < a < π$ nên cos a < 0, do đó từ sin² a + cos² a = 1, suy ra

$\cos a = - \sqrt{1 - \sin^{2} a} = - \sqrt{1 - {(\frac{2}{3})}^{2}} = - \frac{\sqrt{5}}{3}$ .

Ta có $\tan a = \frac{\sin a}{\cos a} = \frac{\frac{2}{3}}{- \frac{\sqrt{5}}{3}} = - \frac{2 \sqrt{5}}{5}$ .

b) $\sin (a + \frac{π}{4})$ $= \sin a \cos \frac{π}{4} + \cos a \sin \frac{π}{4}$ $= \frac{2}{3} . \frac{\sqrt{2}}{2} + (- \frac{\sqrt{5}}{3}) . \frac{\sqrt{2}}{2} = \frac{2 \sqrt{2} - \sqrt{10}}{6}$ .

$\cos (a - \frac{5 π}{6})$ $= \cos a \cos \frac{5 π}{6} + \sin a \sin \frac{5 π}{6}$ $= (- \frac{\sqrt{5}}{3}) . (- \frac{\sqrt{3}}{2}) + \frac{2}{3} . \frac{1}{2} = \frac{\sqrt{15} + 2}{6}$ .

$\tan (a + \frac{2 π}{3})$ $= \frac{\tan a + \tan \frac{2 π}{3}}{1 - \tan a \tan \frac{2 π}{3}} = \frac{- \frac{2 \sqrt{5}}{5} + (- \sqrt{3})}{1 - (- \frac{2 \sqrt{5}}{5}) . (- \sqrt{3})} = \frac{8 \sqrt{5} + 9 \sqrt{3}}{7}$ .

c) $\sin 2 a = 2 \sin a \cos a = 2. \frac{2}{3} . (- \frac{\sqrt{5}}{3}) = - \frac{4 \sqrt{5}}{9}$ .

$\cos 2 a = 2 \cos^{2} a - 1 = 2. {(- \frac{\sqrt{5}}{3})}^{2} - 1 = \frac{1}{9}$ .

Bài 26 trang 15 SBT Toán 11 Tập 1: Cho cos a = 0,2 với π < a < 2π. Tính $\sin \frac{a}{2}$ , $\cos \frac{a}{2}$ , $\tan \frac{a}{2}$ .

Lời giải:

Do π < a < 2π nên $\frac{π}{2} < \frac{a}{2} < π$ . Suy ra $\sin \frac{a}{2} > 0, \cos \frac{a}{2} < 0$ .

Ta có: $\sin^{2} \frac{a}{2} = \frac{1 - \cos a}{2} = \frac{1 - 0,2}{2} = 0,4$ , suy ra $\sin \frac{a}{2} = \frac{\sqrt{10}}{5}$ .

Do đó, $\cos \frac{a}{2} = - \sqrt{1 - \sin^{2} \frac{a}{2}} = - \sqrt{1 - {(\frac{\sqrt{10}}{5})}^{2}} = - \frac{\sqrt{15}}{5}$ .

$\tan \frac{a}{2} = \frac{\sin \frac{a}{2}}{\cos \frac{a}{2}} = \frac{\frac{\sqrt{10}}{5}}{- \frac{\sqrt{15}}{5}} = - \frac{\sqrt{6}}{3}$ .

Bài 27 trang 15 SBT Toán 11 Tập 1: Cho $\tan \frac{a}{2} = \frac{1}{\sqrt{2}}$ . Tính sin a, cos a, tan a.

Lời giải:

Ta có $\sin a = 2 \sin \frac{a}{2} \cos \frac{a}{2} = \frac{2 \sin \frac{a}{2} \cos \frac{a}{2}}{\sin^{2} \frac{a}{2} + \cos^{2} \frac{a}{2}}$ (do $\sin^{2} \frac{a}{2} + \cos^{2} \frac{a}{2} = 1$ )

$= \frac{2 \tan \frac{a}{2}}{\tan^{2} \frac{a}{2} + 1} = \frac{2. \frac{1}{\sqrt{2}}}{{(\frac{1}{\sqrt{2}})}^{2} + 1} = \frac{2 \sqrt{2}}{3}$ .

$\cos a = \cos^{2} \frac{a}{2} - \sin^{2} \frac{a}{2} = \frac{\cos^{2} \frac{a}{2} - \sin^{2} \frac{a}{2}}{\sin^{2} \frac{a}{2} + \cos^{2} \frac{a}{2}}$ $= \frac{1 - \tan^{2} \frac{a}{2}}{\tan^{2} \frac{a}{2} + 1} = \frac{1 - {(\frac{1}{\sqrt{2}})}^{2}}{{(\frac{1}{\sqrt{2}})}^{2} + 1} = \frac{1}{3}$ .

$\tan a = \frac{\sin a}{\cos a} = \frac{\frac{2 \sqrt{2}}{3}}{\frac{1}{3}} = 2 \sqrt{2}$ .

SBT Toán 11 trang 16 Tập 1 (Cánh Diều)

Bài 28 trang 16 SBT Toán 11 Tập 1: Cho cos(a + 2b) = 2cos a. Chứng minh rằng: tan(a + b) tan b = $\frac{- 1}{3}$ .

Lời giải:

Ta có cos(a + 2b) = 2cos a

⇔ cos[(a + b) + b] = 2cos[(a + b) – b]

⇔ cos(a + b) . cos b – sin(a + b) . sin b = 2[cos(a + b) . cos b + sin(a + b) . sin b]

⇔ cos(a + b) . cos b – 2 cos(a + b) . cos b = 2 sin(a + b) . sin b + sin(a + b) . sin b

⇔ – cos(a + b) . cos b = 3 sin(a + b) . sin b

⇔ sin(a + b) . sin b = $- \frac{1}{3}$ cos(a + b) . cos b

$\Leftrightarrow \frac{\sin (a + b) \sin b}{\cos (a + b) \cos b} = - \frac{1}{3}$

⇔ tan(a + b) tan b = $\frac{- 1}{3}$ .

Bài 29 trang 16 SBT Toán 11 Tập 1: Cho tam giác ABC, chứng minh rằng:

a) tan A + tan B + tan C = tan A . tan B . tan C (với điều kiện tam giác ABC không vuông);

b) $\tan \frac{A}{2} . \tan \frac{B}{2} + \tan \frac{B}{2} . \tan \frac{C}{2} + \tan \frac{C}{2} . \tan \frac{A}{2} = 1$ .

Lời giải:

a) Vì tam giác ABC không vuông nên A, B, C khác $\frac{π}{2}$ , do đó tan A, tan B, tan C xác định.

Do A + B + C = π nên A + B = π – C, do đó tan(A + B) = tan(π – C) = tan(– C) = – tanC.

Mà $\tan (A + B) = \frac{\tan A + \tan B}{1 - \tan A \tan B}$ .

Khi đó $\frac{\tan A + \tan B}{1 - \tan A \tan B} = - \tan C$

⇔ tan A + tan B = – tan C . (1 – tan A . tan B)

⇔ tan A + tan B = – tan C + tan A . tan B . tan C

⇔ tan A + tan B + tan C = tan A . tan B . tan C.

b) Ta có $\frac{A + B + C}{2} = \frac{π}{2}$ , suy ra $\frac{A}{2} + \frac{B}{2} = \frac{π}{2} - \frac{C}{2}$ nên $\tan (\frac{A}{2} + \frac{B}{2}) = \cot \frac{C}{2}$

$\Leftrightarrow \frac{\tan \frac{A}{2} + \tan \frac{B}{2}}{1 - \tan \frac{A}{2} . \tan \frac{B}{2}} = \frac{1}{\tan \frac{C}{2}}$

$\Leftrightarrow (\tan \frac{A}{2} + \tan \frac{B}{2}) \tan \frac{C}{2} = 1 - \tan \frac{A}{2} . \tan \frac{B}{2}$

$\Leftrightarrow \tan \frac{A}{2} . \tan \frac{C}{2} + \tan \frac{B}{2} . \tan \frac{C}{2} + \tan \frac{A}{2} . \tan \frac{B}{2} = 1$

$\Leftrightarrow \tan \frac{A}{2} . \tan \frac{B}{2} + \tan \frac{B}{2} . \tan \frac{C}{2} + \tan \frac{C}{2} . \tan \frac{A}{2} = 1$ .

Bài 30 trang 16 SBT Toán 11 Tập 1: Trên một mảnh đất hình vuông ABCD, bác An đặt một chiếc đèn pin tại vị trí A chiếu chùm sáng phân kì sang phía góc C. Bác An nhận thấy góc chiếu sáng của đèn pin giới hạn bởi hai tia AM và AN, ở đó các điểm M, N lần lượt thuộc các cạnh BC, CD sao cho BM = $\frac{1}{2}$ BC, DN = $\frac{1}{3}$ DC (Hình 4).

a) Tính $\tan (\hat{B A M} + \hat{D A N})$ .

b) Góc chiếu sáng của đèn pin bằng bao nhiêu độ?

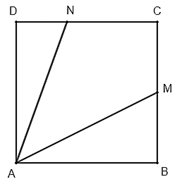
SBT Toán 11 (Cánh diều) Bài 2: Các phép biến đổi lượng giác (ảnh 1)

Hình 4

Lời giải:

a) Trong tam giác vuông ABM, có $\tan \hat{B A M} = \frac{B M}{B A} = \frac{1}{2}$ .

Trong tam giác vuông ADN, có $\tan \hat{D A N} = \frac{D N}{A D} = \frac{D N}{D C} = \frac{1}{3}$ .

Do đó, $\tan (\hat{B A M} + \hat{D A N})$ $= \frac{\tan \hat{B A M} + \tan \hat{D A N}}{1 - \tan \hat{B A M} . \tan \hat{D A N}}$ $= \frac{\frac{1}{2} + \frac{1}{3}}{1 - \frac{1}{2} . \frac{1}{3}} = 1$ .