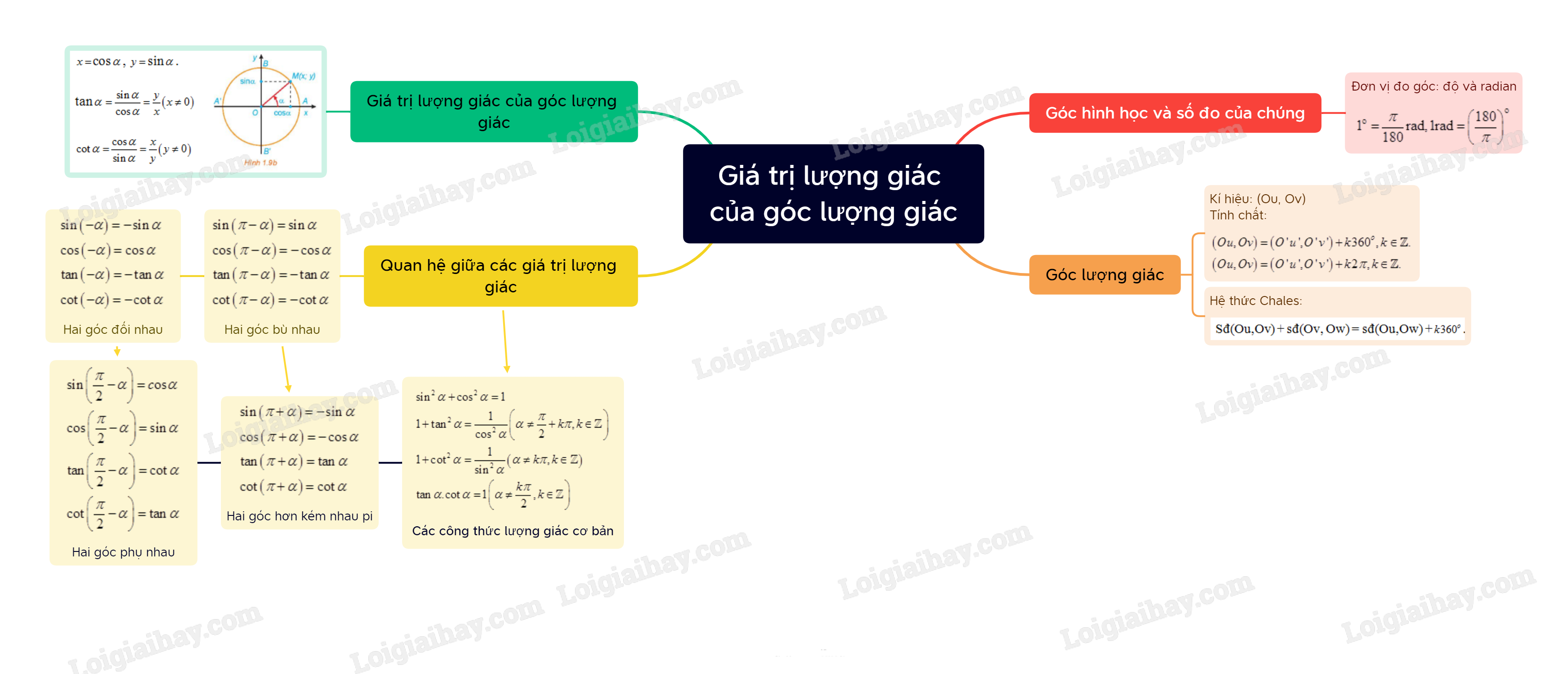
A. Lý thuyết Góc lượng giác. Giá trị lượng giác của góc lượng giác

I. Góc lượng giác

1. Góc hình học và số đo của chúng

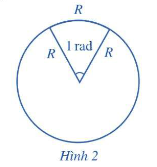
*Nhận xét:

- Đơn vị đo góc: độ hoặc radian (rad).

- Ta có: ${180}^o=\pi$rad, do đó 1 rad $={\left(\frac{180}{\pi }\right)}^o$, $1^o=\left(\frac{\pi }{180}\right)$rad.

- Người ta thường không viết chữ radian hay rad sau số đo góc.

VD: $\frac{\pi }{2}$rad cũng được viết là $\frac{\pi }{2}$.

2. Góc lượng giác và số đo của chúng

a, Khái niệm

- Cho 2 tia Ou, Ov. Nếu tia Om quay chỉ theo chiều dương (hay chỉ theo chiều âm) xuất phát từ Ou đến trùng với tia Ov thì ta nói: Tia Om quét một góc lượng giác với tia đầu Ou và tia cuối Ov.

Kí hiệu: (Ou, Ov).

- Mỗi góc lượng giác được xác định bởi tia đầu Ou, tia cuối Ov và số đo của góc đó.

b, Tính chất

- Cho hai góc lượng giác = và (O’u’,O’v’) có tia đầu trùng nhau $\left(Ou\equiv O^{\prime }{u}^{\prime }\right)$, tia cuối trùng nhau $\left(Ov\equiv O^{\prime }{v}^{\prime }\right)$.

Khi đó, nếu sử dụng đợn vị đo là độ thì ta có:

$\left(Ou,Ov\right)=\left(O^{\prime }{u}^{\prime },O^{\prime }{v}^{\prime }\right)+k{360}^o,k\in \mathbb{Z}.$

Nếu sử dụng đơn vị đo là radian thì:

$\left(Ou,Ov\right)=\left(O^{\prime }{u}^{\prime },O^{\prime }{v}^{\prime }\right)+k2\pi ,k\in \mathbb{Z}.$

* Hệ thức Chasles

Với 3 tia Ou, Ov, Ow bất kì ta có:

 (Ou,Ov) + (Ov, Ow) = (Ou,Ow) $+k2\pi ,k\in \mathbb{Z}.$

II. Giá trị lượng giác của góc lượng giác

1. Đường tròn lượng giác

Trong mặt phẳng toa độ đã được định hướng Oxy, lấy điểm A(1;0). Đường tròn tâm O, bán kính OA = 1 được gọi là đường tròn lượng giác (hay đường tròn đơn vị) gốc A.

2. Giá trị lượng giác của góc lượng giác

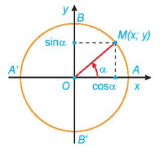
- Trục tung là trục sin, trục hoành là trục côsin.

- Điểm M(x;y) nằm trên đường tròn như hình vẽ. Khi đó:

$x=$cos$\alpha$, $y=$sin$\alpha$.

tan$\alpha$$=\frac{\sin \alpha }{\cos \alpha }=\frac{y}{x}\left(x\ne 0\right)$

$\cot \alpha =\frac{\cos \alpha }{\sin \alpha }=\frac{x}{y}\left(y\ne 0\right)$

* Dấu của các giá trị lượng giác của góc $\alpha$

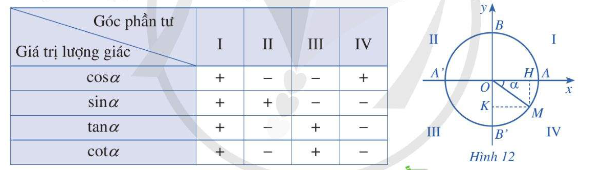
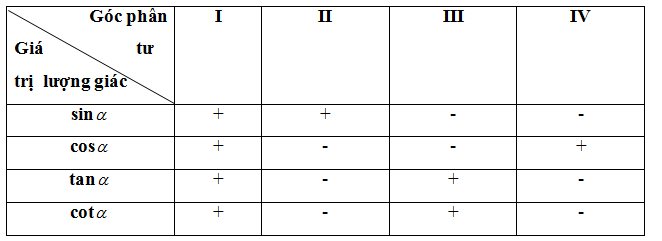
* Các công thức lượng giác cơ bản

$\begin{array}{l}{\sin }^2\alpha +{\cos }^2\alpha =1\\ 1+{\tan }^2\alpha =\frac{1}{{\cos }^2\alpha }\left(\alpha \ne \frac{\pi }{2}+k\pi ,k\in \mathbb{Z}\right)\\ 1+{\cot }^2\alpha =\frac{1}{{\sin }^2\alpha }\left(\alpha \ne k\pi ,k\in \mathbb{Z}\right)\\ \tan \alpha .\cot \alpha =1\left(\alpha \ne \frac{k\pi }{2},k\in \mathbb{Z}\right)\end{array}$

3. Giá trị lượng giác của các góc có liên quan đặc biệt

• Hai góc đối nhau $\alpha$ và $-\alpha$

$\begin{array}{l}\sin \left(-\alpha \right)=-\sin \alpha \\ \cos \left(-\alpha \right)=\cos \alpha \\ \tan \left(-\alpha \right)=-\tan \alpha \\ \cot \left(-\alpha \right)=-\cot \alpha \end{array}$

• Hai góc bù nhau ($\alpha$ và $\pi$-$\alpha$)

$\begin{array}{l}\sin \left(\pi -\alpha \right)=\sin \alpha \\ \cos \left(\pi -\alpha \right)=-\cos \alpha \\ \tan \left(\pi -\alpha \right)=-\tan \alpha \\ \cot \left(\pi -\alpha \right)=-\cot \alpha \end{array}$

• Hai góc phụ nhau ($\alpha$ và $\frac{\pi }{2}$-$\alpha$)

$\begin{array}{l}\sin \left(\frac{\pi }{2}-\alpha \right)=c\mathrm{o}\mathrm{s}\alpha \\ \cos \left(\frac{\pi }{2}-\alpha \right)=\sin \alpha \\ \tan \left(\frac{\pi }{2}-\alpha \right)=\cot \alpha \\ \cot \left(\frac{\pi }{2}-\alpha \right)=\tan \alpha \end{array}$

• Hai góc hơn kém $\pi$($\alpha$ và $\pi$ + $\alpha$)

$\begin{array}{l}\sin \left(\pi +\alpha \right)=-\sin \alpha \\ \cos \left(\pi +\alpha \right)=-\cos \alpha \\ \tan \left(\pi +\alpha \right)=\tan \alpha \\ \cot \left(\pi +\alpha \right)=\cot \alpha \end{array}$

4. Sử dụng máy tính cầm tay để tính giá trị của một góc lượng giác

Đơn vị độ:

Đơn vị radian:

B. Bài tập Góc lượng giác. Giá trị lượng giác của góc lượng giác

Bài 1.

a) Cho $\cos x=\frac{2}{3}$. Tính $A=\frac{\tan x+3\cot x}{\tan x+\cot x}$.

b) Cho $\sin x=-\frac{4}{5}$ và $\frac{3\pi }{2}<x<2\pi$. Tính $B=\frac{\sin x+3\cos x}{\tan x}$.

c) Cho tanx = 3. Tính $C=\frac{\sin x-\cos x}{{\sin }^{3}x+3{\cos }^{3}x+2\sin x}$.

Hướng dẫn giải

a) Ta có $A=\frac{\tan x+3\cot x}{\tan x+\cot x}=\frac{\tan x+3.\frac{1}{\tan x}}{\tan x+\frac{1}{\tan x}}$ (do cosx ≠ 0)

b) Vì $\frac{3\pi }{2}<x<2\pi$ nên cosx > 0.

Ta có sin²x + cos²x = 1, suy ra

.

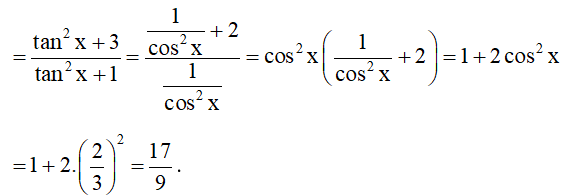
$\iff \cos x=\frac{3}{5}$ (do cosx > 0).

Suy ra $\tan x=\frac{\sin x}{\cos x}=-\frac{4}{5}:\frac{3}{5}=-\frac{4}{3}$.

Khi đó $B=\frac{\sin x+3\cos x}{\tan x}=\frac{-\frac{4}{5}+3.\frac{3}{5}}{-\frac{4}{3}}=-\frac{3}{4}$.

c) Do tanx = 3 nên cosx ≠ 0.

Chia cả tử và mẫu của C cho cos³x, ta được:

$C=\frac{\frac{\sin x}{{\cos }^{3}x}-\frac{\cos x}{{\cos }^{3}x}}{\frac{{\sin }^{3}x}{{\cos }^{3}x}+3+2.\frac{\sin x}{{\cos }^{3}x}}$

Bài 2. Cho tam giác ABC. Chứng minh rằng:

Hướng dẫn giải

Tam giác ABC, có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$

Suy ra $\widehat{A}+2\widehat{B}+\widehat{C}=180°+\widehat{B}$ và $\widehat{B}+\widehat{C}=180°-\widehat{A}$.

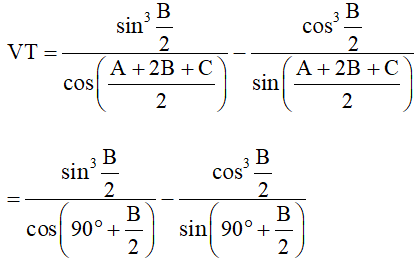
VP = tanA.cot(B + C) = tanA.cot(180° – A) = tanA.(–cotA) = –tanA.cotA = –1 .

Khi đó VT = VP (= –1).

Vậy ta có điều phải chứng minh.

Bài 3. Một bánh xe có bán kính R = 2,4 m quay một góc bằng 30°. Tính độ dài đường đi của một điểm bất kì trên vành bánh xe.

Hướng dẫn giải

Ta xem vành bánh xe là một đường tròn có bán kính R = 2,4 m.

Độ dài đường đi của một điểm bất kì trên vành bánh xe là độ dài của cung tròn có số đo 30°.

Vậy độ dài đường đi cần tìm là $\frac{30°.2\pi .R}{360°}=\frac{30°.2\pi \mathrm{.2,4}}{360°}=\mathrm{0,4}$ m.

Bài 4. Tìm số đo α của góc lượng giác (Ou, Ov) với 0 ≤ α ≤ 2π (0° ≤ α ≤ 360°), biết một góc lượng giác có cùng tia đầu, tia cuối với góc đó có số đo là:

a) $\frac{33\pi }{4}$;

b) $-\frac{291983\pi }{3}$;

c) 3270°.

Hướng dẫn giải

a) Ta có: .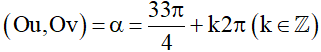

Vì 0 ≤ α ≤ 2π nên $0\le \frac{33\pi }{4}+k2\pi \le 2\pi$.

$\iff -\frac{33\pi }{4}\le k2\pi \le -\frac{25\pi }{4}$.

$\iff -\frac{33}{8}\le k\le -\frac{25}{8}$.

Mà k ∈ ℤ, suy ra k = –4.

Vậy .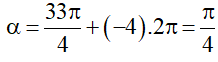

b) Ta có: .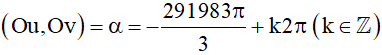

Vì 0 ≤ α ≤ 2π nên $0\le -\frac{291983\pi }{3}+k2\pi \le 2\pi$.

$\iff \frac{291983\pi }{3}\le k2\pi \le \frac{291989\pi }{3}$.

$\iff \frac{291983}{6}\le k\le \frac{291989}{6}$.

Mà k ∈ ℤ, suy ra k = 48664.

Vậy $\alpha =-\frac{291983\pi }{3}+48664.2\pi =\frac{\pi }{3}$.

c) Ta có: (Ou,Ov) = α = 3270° + k.360° (k ∈ ℤ).

Vì 0° ≤ α ≤ 360° nên 0° ≤ 3270° + k.360° ≤ 360°.

⇔ –3270° ≤ k.360° ≤ –2910°.

$\iff -\frac{109}{12}\le k\le -\frac{97}{12}$.

Mà k ∈ ℤ, suy ra k = –9.

Vậy α = 3270° + (–9).360° = 30°.

Bài 5. Tìm các giá trị lượng giác của góc lượng giác $\alpha =\frac{3\pi }{4}$.

Hướng dẫn giải

Lấy điểm M trên đường tròn lượng giác sao cho $\left(OA,OM\right)=\alpha =\frac{3\pi }{4}$ (hình vẽ).

Gọi H, K lần lượt là hình chiếu của điểm M lên các trục Ox, Oy.

Khi đó $\widehat{AOM}=\frac{3\pi }{4}$.

Suy ra $\widehat{BOM}=\widehat{KOM}=\frac{3\pi }{4}-\frac{\pi }{2}=\frac{\pi }{4}$.

Tam giác KOM vuông tại K, có:

⦁ $OK=OM.\cos \widehat{KOM}=1.\cos \frac{\pi }{4}=\frac{\sqrt{2}}{2}$;

⦁ $MK=OM.\sin \widehat{KOM}=1.\sin \frac{\pi }{4}=\frac{\sqrt{2}}{2}$.

Suy ra tọa độ .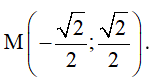

Vậy $\sin \frac{3\pi }{4}=-\frac{\sqrt{2}}{2}$; $\cos \frac{3\pi }{4}=\frac{\sqrt{2}}{2}$; $\tan \frac{3\pi }{4}=\frac{\sin \frac{3\pi }{4}}{\cos \frac{3\pi }{4}}=-1$ và $\cot \frac{3\pi }{4}=\frac{\cos \frac{3\pi }{4}}{\sin \frac{3\pi }{4}}=-1$.

Xem thêm Lý thuyết  các bài Toán 11 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 2: Các phép biến đổi lượng giác

Lý thuyết Bài 3: Hàm số lượng giác và đồ thị

Lý thuyết Bài 4: Phương trình lượng giác cơ bản

Lý thuyết Bài 1: Dãy số