Toptailieu biên soạn và giới thiệu lời giải Toán 11 Bài 3 (Cánh diều): Hàm số lượng giác và đồ thị hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi SGK Toán 11 Bài 3 từ đó học tốt môn Toán 11.

Giải Bài 3: Hàm số lượng giác và đồ thị  SGK Toán 11 Tập 1 (Cánh Diều)

Giải Toán 11 trang 22 Tập 1

Câu hỏi khởi động trang 22 Toán 11 Tập 1: Guồng nước (hay còn gọi là cọn nước) không chỉ là công cụ phục vụ sản xuất nông nghiệp, mà đã trở thành hình ảnh quen thuộc của bản làng và là một nét văn hoá đặc trưng của đồng bào dân tộc miền núi phía Bắc.

Một chiếc guồng nước có dạng hình tròn bán kính 2,5 m; trục của nó đặt cách mặt nước 2 m. Khi guồng quay đều, khoảng cách h (m) từ một ống đựng nước gắn tại một điểm của guồng đến mặt nước được tính theo công thức h = |y|, trong đó y = 2,5sin$\left(2\pi x-\frac{\pi }{2}\right)$+2, với x (phút) là thời gian quay của guồng (x ≥ 0).

(Nguồn: Đại số và Giải tích 11 Nâng cao, NXBGD Việt Nam, 2020).

Khoảng cách h phụ thuộc vào thời gian quay x như thế nào?

Lời giải:

Khoảng cách h phụ thuộc vào thời gian quay x theo biểu thức:

h = |2,5sin$\left(2\pi x-\frac{\pi }{2}\right)$+2|

I. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn

Hoạt động 1 trang 22 Toán 11 Tập 1: a) Cho hàm số f(x) = x².

• Với x ∈ ℝ, hãy so sánh f(‒x) và f(x).

• Quan sát parabol (P) là đồ thị của hàm số f(x) = x² (Hình 19) và cho biết trục đối xứng của (P) là đường thẳng nào.

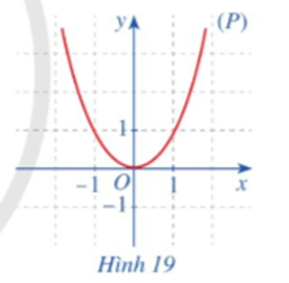
b) Cho hàm số g(x) = x.

• Với x ∈ ℝ, hãy so sánh g(‒x) và ‒g(x).

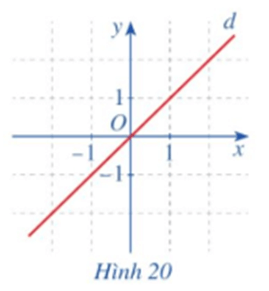
• Quan sát đường thẳng d là đồ thị của hàm số g(x) = x (Hình 20) và cho biết gốc toạ độ O có là tâm đối xứng của đường thẳng d hay không.

Lời giải:

a) Xét hàm số f(x) = x².

• Với x ∈ ℝ, ta có: f(‒x) = (‒x)² = x².

Do đó f(‒x) = f(x).

• Trục đối xứng của (P) là đường thẳng x = 0, hay chính là trục Oy.

b) Xét hàm số g(x) = x.

• Với x ∈ ℝ, ta có: g(‒x) = ‒x và ‒g(x) = ‒x.

Do đó g(‒x) = ‒g(x).

• Gốc tọa độ O là tâm đối xứng của đường thẳng d.

Giải Toán 11 trang 23 Tập 1

Luyện tập 1 trang 23 Toán 11 Tập 1: a) Chứng tỏ rằng hàm số g(x) = x³ là hàm số lẻ.

b) Cho ví dụ về hàm số không là hàm số chẵn và cũng không là hàm số lẻ.

Lời giải:

a) Xét hàm số g(x) = x³ có tập xác định D = ℝ.

∀x ∈ ℝ thì ‒x ∈ ℝ, ta có: g(‒x) = (‒x)³ = ‒x³ = ‒g(x).

Do đó hàm số g(x) = x³ là hàm số lẻ.

b) Ví dụ về hàm số không là hàm số chẵn và cũng không là hàm số lẻ:

f(x) = x² + x; g(x) = 2x³ – 3x²; …

Hoạt động 2 trang 23 Toán 11 Tập 1: Cho hàm số y = f(x) xác định trên ℝ và có đồ thị như Hình 21.

a) Có nhận xét gì về đồ thị hàm số trên mỗi đoạn [a ; a + T], [a + T; a + 2T], [a – T; a]?

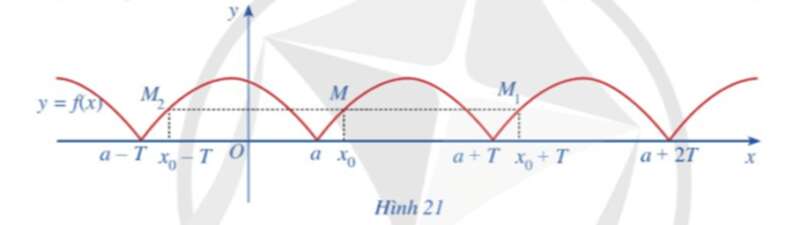
b) Lấy điểm M(x₀; f(x₀)) thuộc đồ thị hàm số với x₀ ∈ [a; a + T]. So sánh mỗi giá trị f(x₀ + T), f(x₀ − T) với f(x₀).

Lời giải:

a) Đồ thị hàm số trên mỗi đoạn [a ; a + T], [a + T; a + 2T], [a – T; a] có dạng giống nhau.

b) Ta có f(x₀ + T) = f(x₀);

f(x₀ − T) = f(x₀).

Luyện tập 2 trang 23 Toán 11 Tập 1: Cho ví dụ về hàm số tuần hoàn.

Lời giải:

Ví dụ về hàm số tuần hoàn:

Cho T là một số hữu tỉ và hàm số f(x) được cho bởi công thức sau:

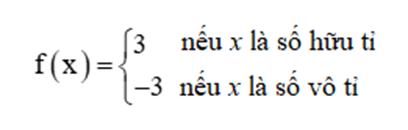
Ta thấy, hàm số xác định trên ℝ. Xét một số thực tùy ý.

Nếu x là số hữu tỉ thì x + T cũng là số hữu tỉ;

Nếu x là số vô tỉ thì x + T cũng là số vô tỉ.

Do đó f(x + T) = f(x) với mọi x.

Vậy hàm số f(x) là hàm số tuần hoàn.

I. Hàm số y = sinx

Giải Toán 11 trang 24 Tập 1

Hoạt động 3 trang 24 Toán 11 Tập 1: Với mỗi số thực x, tồn tại duy nhất điểm M trên đường tròn lượng giác sao cho (OA, OM) = x (rad) (Hình 22). Hãy xác định sinx.

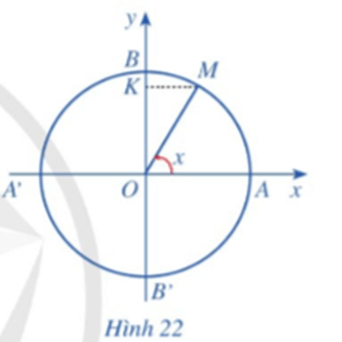
Lời giải:

Giả sử tung độ của điểm M là y.

Khi đó ta có sinx = y.

Hoạt động 4 trang 24 Toán 11 Tập 1: Cho hàm số y = sinx.

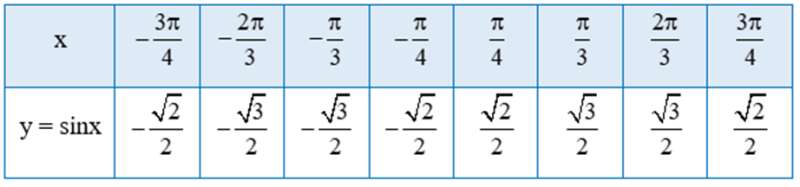
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x ; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; sinx) với x ∈ [‒π; π] và nối lại ta được đồ thị hàm số y = sinx trên đoạn [‒π; π] (Hình 23).

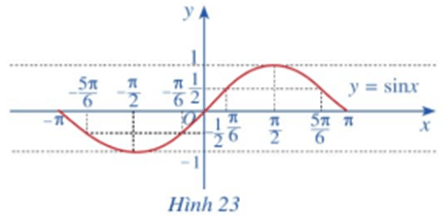
c) Làm tương tự như trên đối với các đoạn [‒3π; ‒π], [π; 3π], …, ta có đồ thị hàm số y = sin x trên ℝ được biểu diễn ở Hình 24.

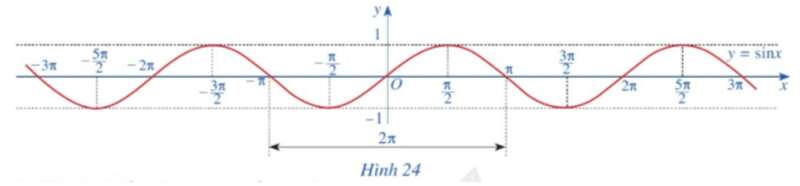
Lời giải:

a) Thay từng giá trị của x vào hàm số y = sinx ta có bảng sau:

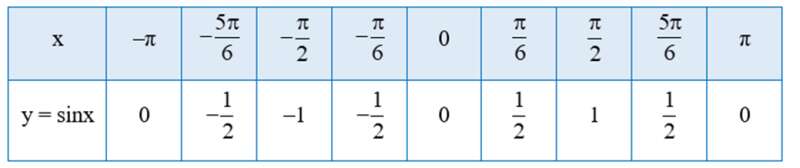
b) Lấy thêm một số điểm (x; sinx) với x ∈ [‒π; π] trong bảng sau và nối lại ta được đồ thị hàm số y = sinx trên đoạn [‒π; π] (hình vẽ).

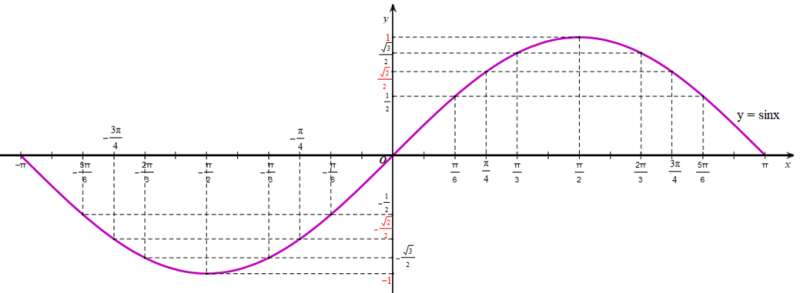
c) Làm tương tự như trên đối với các đoạn [‒3π; ‒π], [π; 3π], …, ta có đồ thị hàm số y = sin x trên ℝ được biểu diễn ở hình vẽ sau:

Giải Toán 11 trang 25 Tập 1

Hoạt động 5 trang 25 Toán 11 Tập 1: Quan sát đồ thị hàm số y = sinx ở Hình 24.

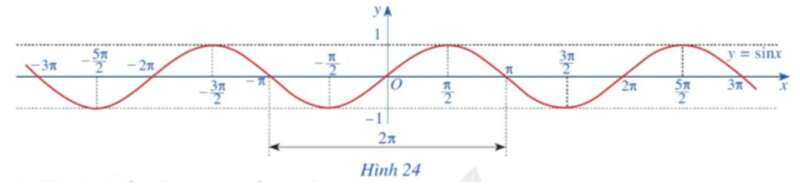
a) Nêu tập giá trị của hàm số y = sinx.

b) Gốc toạ độ có là tâm đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số y = sinx.

c) Bằng cách dịch chuyển đồ thị hàm số y = sinx trên đoạn [‒π; π] song song với trục hoành sang phải theo đoạn có độ dài 2π, ta có nhận được đồ thị hàm số y = sinx trên đoạn [π; 3π] hay không? Hàm số y = sinx có tuần hoàn hay không?

d) Tìm khoảng đồng biến, nghịch biến của hàm số y = sinx.

Lời giải:

a) Tập giá trị của hàm số y = sinx là [‒1; 1].

b) Gốc toạ độ O là tâm đối xứng của đồ thị hàm số.

Do đó hàm số y = sinx là hàm số lẻ.

c)

‒ Bằng cách dịch chuyển đồ thị hàm số y = sinx trên đoạn [‒π; π] song song với trục hoành sang phải theo đoạn có độ dài 2π, ta sẽ nhận được đồ thị hàm số y = sinx trên đoạn [π; 3π].

Làm tương tự như trên ta sẽ được đồ thị hàm số y = sinx trên ℝ.

‒ Xét hàm số f(x) = y = sinx trên ℝ, với T = 2π và x ∈ ℝ ta có:

• x + 2π ∈ ℝ và x – 2π ∈ ℝ;

• f(x + 2π) = f(x)

Do đó hàm số y = sinx là hàm số tuần hoàn với chu kì T = 2π.

d) Quan sát đồ thị hàm số y = sinx ta thấy:

• Hàm số đồng biến trên mỗi khoảng $\left(-\frac{5\pi }{2};-\frac{3\pi }{2}\right);\left(-\frac{\pi }{2};\frac{\pi }{2}\right);\left(\frac{3\pi }{2};\frac{5\pi }{2}\right);\mathrm{...}$

Ta có: $\left(-\frac{5\pi }{2};-\frac{3\pi }{2}\right)=\left(-\frac{\pi }{2}-2\pi ;\frac{\pi }{2}-2\pi \right)$;

$\left(\frac{3\pi }{2};\frac{5\pi }{2}\right)=\left(-\frac{\pi }{2}+2\pi ;\frac{\pi }{2}+2\pi \right)$;

…

Do đó ta có thể viết hàm số đồng biến trên mỗi khoảng $\left(-\frac{\pi }{2}+k2\pi ;\frac{\pi }{2}+k2\pi \right)$ với k ∈ ℤ.

• Hàm số nghịch biến trên mỗi khoảng $\left(-\frac{7\pi }{2};-\frac{5\pi }{2}\right);\left(-\frac{3\pi }{2};-\frac{\pi }{2}\right);\left(\frac{\pi }{2};\frac{3\pi }{2}\right);\mathrm{...}$

Ta có: $\left(-\frac{3\pi }{2};-\frac{\pi }{2}\right)=\left(\frac{\pi }{2}-2\pi ;\frac{3\pi }{2}-2\pi \right)$;

…

Do đó ta có thể viết hàm số nghịch biến trên mỗi khoảng $\left(\frac{\pi }{2}+k2\pi ;\frac{3\pi }{2}+k2\pi \right)$ với k ∈ ℤ.

Luyện tập 3 trang 25 Toán 11 Tập 1: Hàm số y = sinx đồng biến hay nghịch biến trên khoảng $\left(-\frac{7\pi }{2};-\frac{5\pi }{2}\right)$?

Lời giải:

Do $\left(-\frac{7\pi }{2};-\frac{5\pi }{2}\right)=\left(\frac{\pi }{2}-4\pi ;\frac{3\pi }{2}-4\pi \right)=\left(\frac{\pi }{2}+\left(-2\right).2\pi ;\frac{3\pi }{2}+\left(-2\right).2\pi \right)$ nên hàm số y = sinx nghịch biến trên khoảng $\left(-\frac{7\pi }{2};-\frac{5\pi }{2}\right)$.

III. Hàm số y = cosx

Giải Toán 11 trang 26 Tập 1

Hoạt động 6 trang 26 Toán 11 Tập 1: Với mỗi số thực x, tồn tại duy nhất điểm M trên đường tròn lượng giác sao cho (OA, OM) = x (rad) (Hình 25). Hãy xác định cosx.

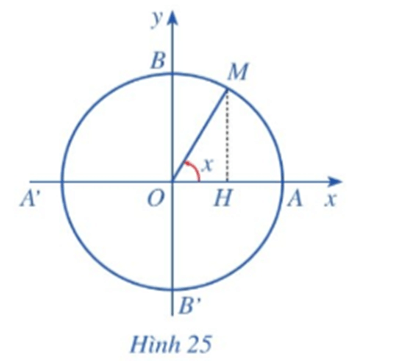
Lời giải:

Giả sử hoành độ của điểm M là y.

Khi đó ta có sinx = y.

Hoạt động 7 trang 26 Toán 11 Tập 1: Cho hàm số y = cosx.

a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

b) Trong mặt phẳng toạ độ Oxy, hãy biểu diễn các điểm (x ; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x ; cosx) với x ∈ [‒π; π] và nối lại ta được đồ thị hàm số y = cosx trên đoạn [‒π; π] (Hình 26).

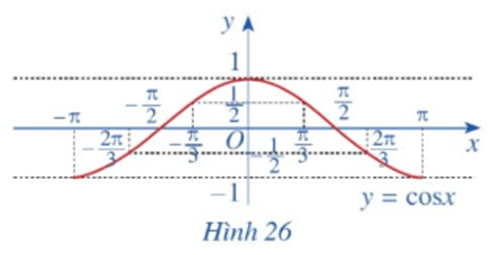
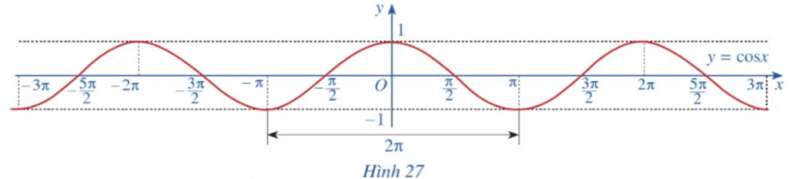
c) Làm tương tự như trên đối với các đoạn [‒3π; ‒π], [π; 3π], ta có đồ thị hàm số y = cosx trên ℝ được biểu diễn ở Hình 27.

Lời giải:

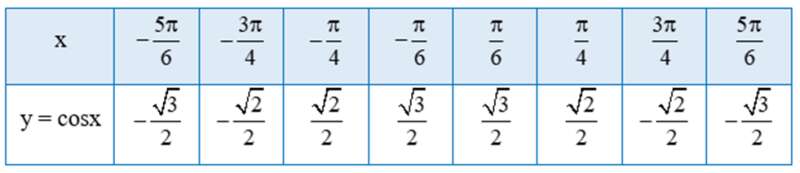
a) Thay từng giá trị của x vào hàm số y = cosx ta có bảng sau:

b) Lấy thêm một số điểm (x; cosx) với x ∈ [‒π; π] trong bảng sau và nối lại ta được đồ thị hàm số y = cosx trên đoạn [‒π; π] (hình vẽ).

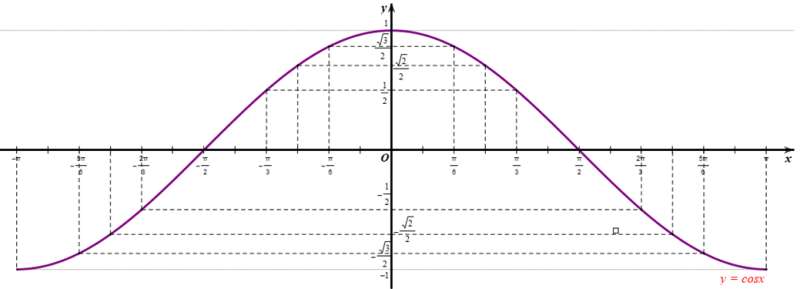
c) Làm tương tự như trên đối với các đoạn [‒3π; ‒π], [π; 3π], …, ta có đồ thị hàm số y = cosx trên ℝ được biểu diễn ở hình vẽ sau:

Giải Toán 11 trang 27 Tập 1

Hoạt động 8 trang 27 Toán 11 Tập 1: Quan sát đồ thị hàm số y = cosx ở Hình 27.

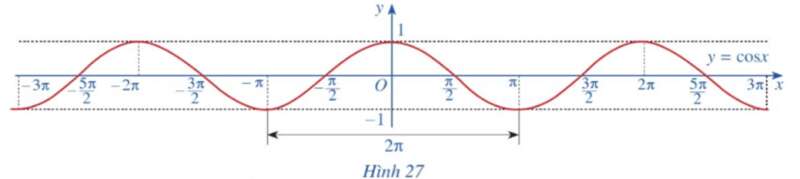
a) Nêu tập giá trị của hàm số y = cosx.

b) Trục tung có là trục đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số y = cosx.

c) Bằng cách dịch chuyển đồ thị hàm số y = cosx trên đoạn [‒π; π] song song với trục hoành sang phải theo đoạn có độ dài 2π, ta nhận được đồ thị hàm số y = cosx trên đoạn [π; 3π] hay không? Hàm số y = cosx có tuần hoàn hay không?

d) Tìm khoảng đồng biến, nghịch biến của hàm số y = cosx.

Lời giải:

a) Tập giá trị của hàm số y = cosx là [‒1; 1].

b) Trục tung là trục đối xứng của đồ thị hàm số.

Do đó hàm số y = cosx là hàm số chẵn.

c)

‒ Bằng cách dịch chuyển đồ thị hàm số y = cosx trên đoạn [‒π; π] song song với trục hoành sang phải theo đoạn có độ dài 2π, ta sẽ nhận được đồ thị hàm số y = cosx trên đoạn [π; 3π].

Làm tương tự như trên ta sẽ được đồ thị hàm số y = cosx trên ℝ.

‒ Xét hàm số f(x) = y = cosx trên ℝ, với T = 2π và x ∈ ℝ ta có:

• x + 2π ∈ ℝ và x – 2π ∈ ℝ;

• f(x + 2π) = f(x)

Do đó hàm số y = cosx là hàm số tuần hoàn với chu kì T = 2π.

d) Quan sát đồ thị hàm số y = cosx ta thấy:

• Hàm số đồng biến trên mỗi khoảng (‒3π; ‒2π); (‒π; 0); (π; 2π); …

Ta có: (‒3π; ‒2π) = (‒π ‒ 2π; 0 ‒ 2π);

(π; 2π) = (‒π + 2π; 0 + 2π);

…

Do đó ta có thể viết hàm số đồng biến trên mỗi khoảng (‒π + k2π; k2π) với k ∈ ℤ.

• Hàm số nghịch biến trên mỗi khoảng (‒2π; ‒π); (0; π); (2π; 3π); …

Ta có: (‒2π; ‒π) = (0 ‒ 2π; π ‒ 2π);

(2π; 3π) = (0 + 2π; π + 2π);

…

Do đó ta có thể viết hàm số nghịch biến trên mỗi khoảng (k2π; π + k2π) với k ∈ ℤ.

Luyện tập 4 trang 27 Toán 11 Tập 1: Hàm số y = cosx đồng biến hay nghịch biến trên khoảng (‒2π; ‒π)?

Lời giải:

Do (‒2π; ‒π) = (0 – 2π; π – 2π) nên hàm số nghịch biến trên khoảng (‒2π; ‒π).

IV. Hàm số y = tanx

Hoạt động 9 trang 27 Toán 11 Tập 1: Xét tập hợp D = R\$\left(\frac{\pi }{2}+k\pi |k\in \mathbb{Z}\right)$. Với mỗi số thực x ∈ D, hãy nêu định nghĩa tanx.

Lời giải:

Nếu cosx ≠ 0, tức $x\in ℝ\backslash \left(\frac{\pi }{2}+k\pi |k\in \mathbb{Z}\right)$ hay x ∈ D thì ta có: tanx = $\frac{\sin x}{\cos x}$.

Giải Toán 11 trang 28 Tập 1

Hoạt động 10 trang 28 Toán 11 Tập 1: Cho hàm số y = tanx.

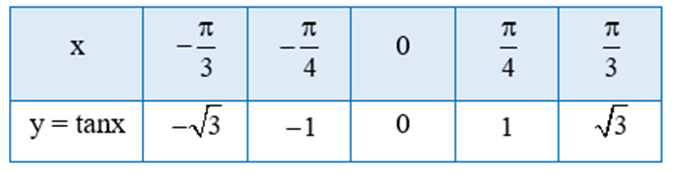
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

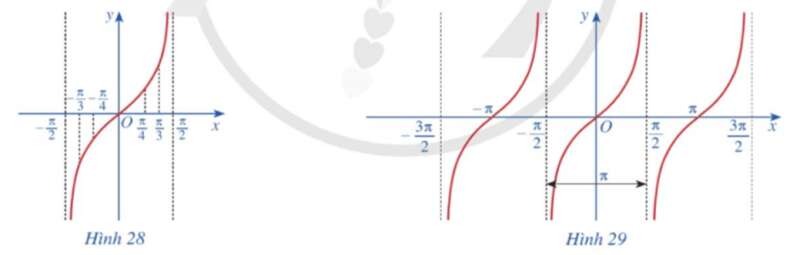
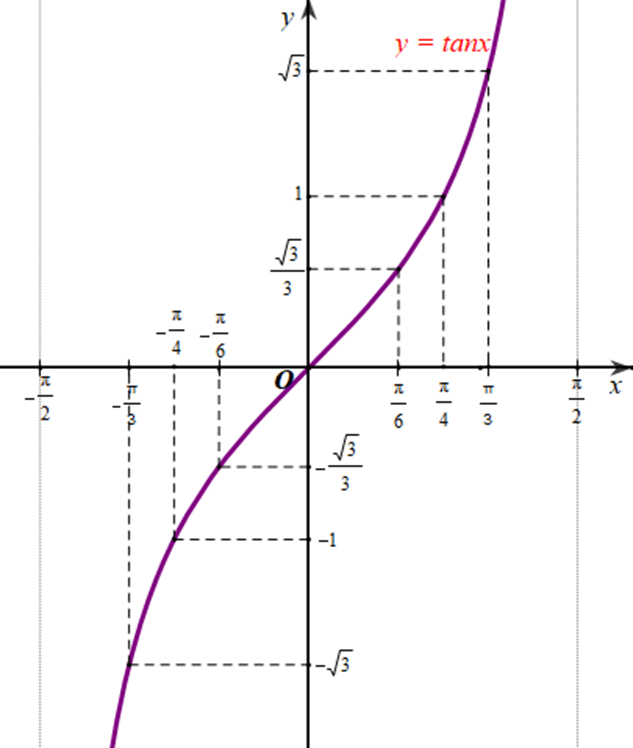
b) Trong mặt phẳng toạ độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; tanx) với $x\in \left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ và nối lại ta được đồ thị hàm số y = tan x trên khoảng $x\in \left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ (Hình 28).

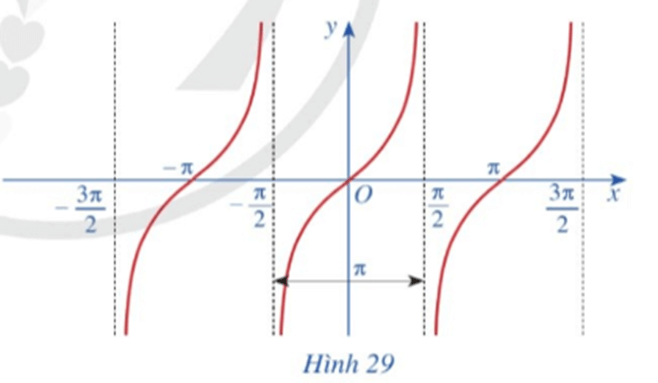
c) Làm tương tự như trên đối với các khoảng $\left(\frac{\pi }{2};\frac{3\pi }{2}\right),\left(-\frac{3\pi }{2};-\frac{\pi }{2}\right)$, …, ta có đồ thị hàm số y = tan x trên D được biểu diễn ở Hình 29.

Lời giải:

a) Thay từng giá trị của x vào hàm số y = tanx ta có bảng sau:

b) Lấy thêm một số điểm (x; tanx) với $x\in \left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ trong bảng sau và nối lại ta được đồ thị hàm số y = tanx trên khoảng $x\in \left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ (hình vẽ).

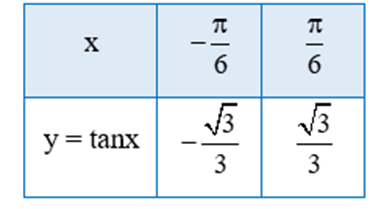
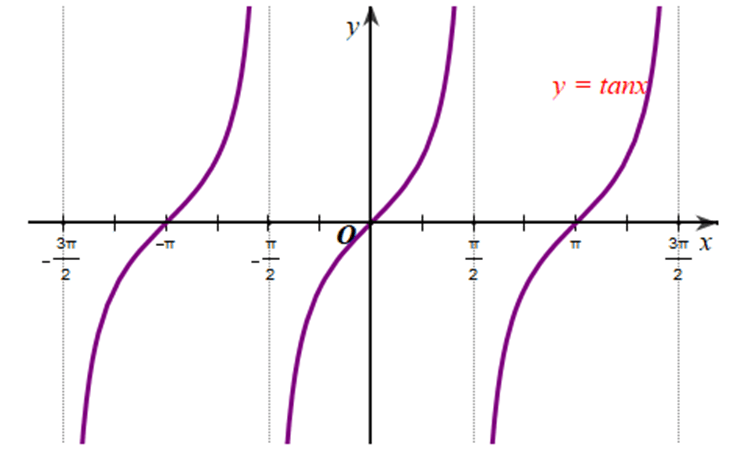
c) Làm tương tự như trên đối với các $\left(\frac{\pi }{2};\frac{3\pi }{2}\right),\left(-\frac{3\pi }{2};-\frac{\pi }{2}\right)$, …, ta có đồ thị hàm số y = tanx trên D được biểu diễn ở hình vẽ sau:

Hoạt động 11 trang 28 Toán 11 Tập 1: Quan sát đồ thị hàm số y = tanx ở Hình 29.

a) Nêu tập giá trị của hàm số y = tanx.

b) Gốc toạ độ có là tâm đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số y = tanx.

c) Bằng cách dịch chuyển đồ thị hàm số y = tanx trên khoảng $\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ song song với trục hoành sang phải theo đoạn có độ dài π, ta nhận được đồ thị hàm số y = tanx trên khoảng $\left(\frac{\pi }{2};\frac{3\pi }{2}\right)$ hay không? Hàm số y = tanx có tuần hoàn hay không?

d) Tìm khoảng đồng biến, nghịch biến của hàm số y = tanx.

Lời giải:

a) Tập giá trị của hàm số y = tanx là ℝ.

b) Gốc toạ độ là tâm đối xứng của đồ thị hàm số y = tanx.

Do đó hàm số y = tanx là hàm số lẻ.

c)

‒ Bằng cách dịch chuyển đồ thị hàm số y = tanx trên khoảng $\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ song song với trục hoành sang phải theo đoạn có độ dài π, ta sẽ nhận được đồ thị hàm số y = tanx trên khoảng $\left(\frac{\pi }{2};\frac{3\pi }{2}\right)$.

Làm tương tự như trên ta sẽ được đồ thị hàm số y = tanx trên R\$\left(\frac{\pi }{2}+k\pi |k\in \mathbb{Z}\right)$.

‒ Xét hàm số f(x) = y = tanx trên D = R\$\left(\frac{\pi }{2}+k\pi |k\in \mathbb{Z}\right)$, với T = π và x ∈ D ta có:

• x + π ∈ D và x – π ∈ D;

• f(x + π) = f(x)

Do đó hàm số y = tanx là hàm số tuần hoàn với chu kì T = π.

d) Quan sát đồ thị hàm số y = tanx ở Hình 29, ta thấy: đồ thị hàm số đồng biến trên mỗi khoảng $\left(-\frac{3\pi }{2};-\frac{\pi }{2}\right);\left(-\frac{\pi }{2};\frac{\pi }{2}\right);\left(\frac{\pi }{2};\frac{3\pi }{2}\right)$;...

Ta có: $\left(-\frac{3\pi }{2};-\frac{\pi }{2}\right)=\left(-\frac{\pi }{2}-\pi ;\frac{\pi }{2}-\pi \right)$;

$\left(\frac{\pi }{2};\frac{3\pi }{2}\right)=\left(-\frac{\pi }{2}+\pi ;\frac{\pi }{2}+\pi \right)$;

…

Do đó ta có thể viết đồ thị hàm số y = tanx đồng biến trên mỗi khoảng $\left(-\frac{\pi }{2}+k\pi ;\frac{\pi }{2}+k\pi \right)$ với k ∈ ℤ.

Giải Toán 11 trang 29 Tập 1

Luyện tập 5 trang 29 Toán 11 Tập 1: Với mỗi số thực m, tìm số giao điểm của đường thẳng y = m và đồ thị hàm số y = tanx trên khoảng $\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$.

Lời giải:

Xét đồ thị của hàm số y = m và đồ thị của hàm số y = tanx trên khoảng $\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ (hình vẽ).

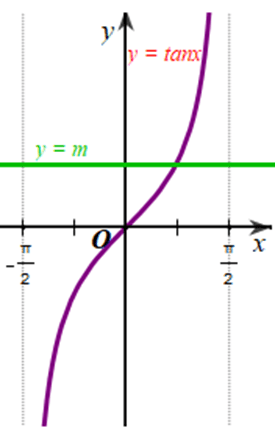
Từ đồ thị của hai hàm số trên hình vẽ, ta thấy mọi m ∈ ℝ thì hai đồ thị trên luôn cắt nhau tại 1 điểm.

Vậy số giao điểm của đường thẳng y = m (m ∈ ℝ) và đồ thị hàm số y = tanx trên khoảng $\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ là 1.

V. Hàm số y = cotx

Hoạt động 12 trang 29 Toán 11 Tập 1: Xét tập hợp E = ℝ \ {kπ | k ∈ ℤ}. Với mỗi số thực x ∈ E, hãy nêu định nghĩa cotx.

Lời giải:

Nếu sinx ≠ 0, tức x ∈ ℝ \ {kπ | k ∈ ℤ} hay x ∈ E thì ta có: cot x = $\frac{\cos x}{\sin x}$.

Hoạt động 13 trang 29 Toán 11 Tập 1: Cho hàm số y = cotx.

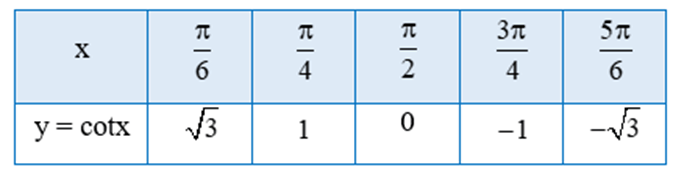
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

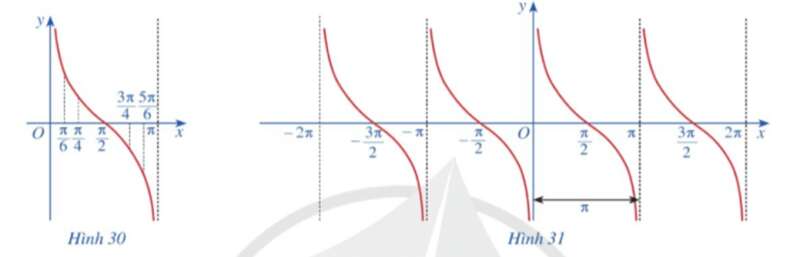
b) Trong mặt phẳng toạ độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; cotx) với x ∈ (0; π) và nối lại ta được đồ thị hàm số y = cotx trên khoảng (0; π) (Hình 30).

c) Làm tương tự như trên đối với các khoảng (π; 2π), (‒π; 0), (‒2π; ‒π), …, ta có đồ thị hàm số y = cotx trên E được biểu diễn ở Hình 31.

Lời giải:

a) Thay từng giá trị của x vào hàm số y = cotx ta có bảng sau:

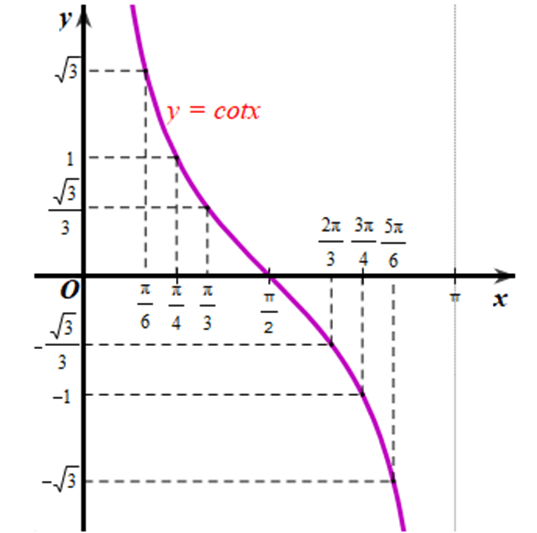
b) Lấy thêm một số điểm (x; cotx) với x ∈ (0; π) trong bảng sau và nối lại ta được đồ thị hàm số y = cotx trên khoảng x ∈ (0; π) (hình vẽ).

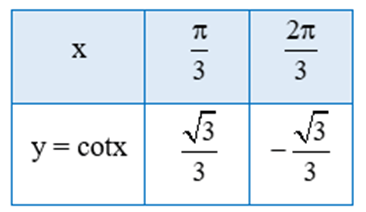
c) Làm tương tự như trên đối với các $\left(\frac{\pi }{2};\frac{3\pi }{2}\right),\left(-\frac{3\pi }{2};-\frac{\pi }{2}\right)$, …, ta có đồ thị hàm số y = tanx trên D được biểu diễn ở hình vẽ sau:

Giải Toán 11 trang 30 Tập 1

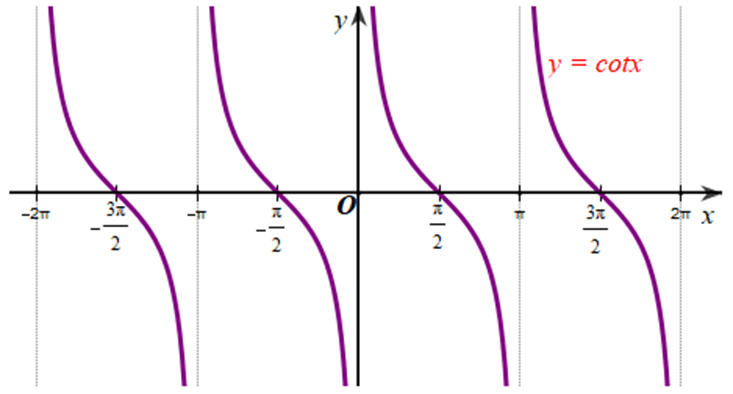
Hoạt động 14 trang 30 Toán 11 Tập 1: Quan sát đồ thị hàm số y = cotx ở Hình 31.

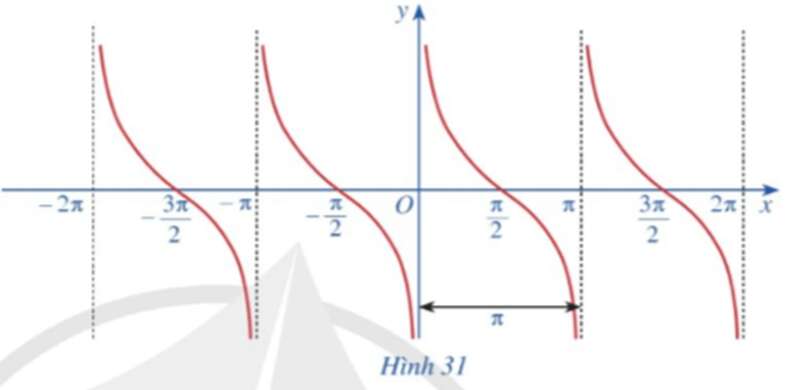
a) Nêu tập giá trị của hàm số y = cotx.

b) Gốc toạ độ có là tâm đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số y = cotx.

c) Bằng cách dịch chuyển đồ thị hàm số y = cotx trên khoảng (0; π) song song với trục hoành sang phải theo đoạn có độ dài π, ta nhận được đồ thị hàm số y = cotx trên khoảng (π; 2π) hay không? Hàm số y = cotx có tuần hoàn hay không?

d) Tìm khoảng đồng biến, nghịch biến của hàm số y = cotx.

Lời giải:

a) Tập giá trị của hàm số y = cotx là ℝ.

b) Gốc toạ độ là tâm đối xứng của đồ thị hàm số y = cotx.

Do đó hàm số y = cotx là hàm số lẻ.

c)

‒ Bằng cách dịch chuyển đồ thị hàm số y = cotx trên khoảng (0; π) song song với trục hoành sang phải theo đoạn có độ dài π, ta sẽ nhận được đồ thị hàm số y = cotx trên khoảng (π; 2π).

Làm tương tự như trên ta sẽ được đồ thị hàm số y = cotx trên ℝ \ {kπ | k ∈ ℤ}.

‒ Xét hàm số f(x) = y = cotx trên D = ℝ \ {kπ | k ∈ ℤ}, với T = π và x ∈ D ta có:

• x + π ∈ D và x – π ∈ D;

• f(x + π) = f(x)

Do đó hàm số y = cotx là hàm số tuần hoàn với chu kì T = π.

d) Quan sát đồ thị hàm số y = cotx ở Hình 31, ta thấy: đồ thị hàm số nghịch biến trên mỗi khoảng (‒2π; ‒π); (‒π; 0); (0; π); (π; 2π); …

Ta có: (‒2π; ‒π) = (0 ‒ 2π; π – 2π);

(‒π; 0) = (0 – π; π ‒ π);

(π; 2π) = (0 + π; π + π);

…

Do đó ta có thể viết đồ thị hàm số y = cotx nghịch biến trên mỗi khoảng (kπ; π + kπ) với k ∈ ℤ.

Luyện tập 6 trang 30 Toán 11 Tập 1: Với mỗi số thực m, tìm số giao điểm của đường thẳng y = m và đồ thị hàm số y = cotx trên khoảng (0; π).

Lời giải:

Xét đồ thị của hàm số y = m và đồ thị của hàm số y = cotx trên khoảng (0; π) (hình vẽ).

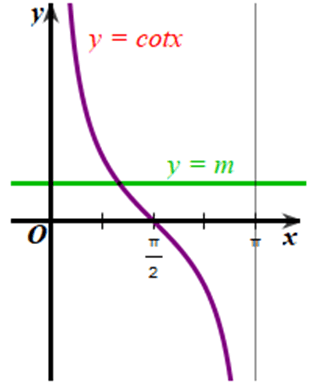
Từ đồ thị của hai hàm số trên hình vẽ, ta thấy mọi m ∈ ℝ thì hai đồ thị trên luôn cắt nhau tại 1 điểm.

Vậy số giao điểm của đường thẳng y = m (m ∈ ℝ) và đồ thị hàm số y = cotx trên khoảng (0; π) là 1.

Bài tập

Giải Toán 11 trang 31 Tập 1

Bài 1 trang 31 Toán 11 Tập 1: Dùng đồ thị hàm số, tìm giá trị của x trên đoạn [‒2π; 2π] để:

a) Hàm số y = sinx nhận giá trị bằng 1;

b) Hàm số y = sinx nhận giá trị bằng 0;

c) Hàm số y = cosx nhận giá trị bằng ‒1;

d) Hàm số y = cosx nhận giá trị bằng 0.

Lời giải:

a) Đồ thị hàm số y = sinx:

Quan sát đồ thị hàm số y = sinx trên đoạn [‒2π; 2π] ta thấy hàm số y = sinx nhận giá trị bằng 1 tại x$\in \left(-\frac{3\pi }{2};\frac{\pi }{2}\right)$.

b) Đồ thị hàm số y = sinx:

Quan sát đồ thị hàm số y = sinx trên đoạn [‒2π; 2π] ta thấy hàm số y = sinx nhận giá trị bằng 0 tại x ∈ {‒2π; ‒π; 0; π; 2π}.

c) Đồ thị hàm số y = cosx:

Quan sát đồ thị hàm số y = cosx trên đoạn [‒2π; 2π] ta thấy hàm số y = cosx nhận giá trị bằng ‒1 tại x ∈ {‒π; π}.

d) Đồ thị hàm số y = cosx:

Quan sát hai đồ thị hàm số y = cosx trên đoạn [‒2π; 2π] ta thấy hàm số y = cosx nhận giá trị bằng 0 tại x$\in \left(-\frac{3\pi }{2};-\frac{\pi }{2};\frac{\pi }{2};\frac{3\pi }{2}\right)$.

Bài 2 trang 31 Toán 11 Tập 1: Dùng đồ thị hàm số, tìm giá trị của x trên khoảng $\left(-\pi ;\frac{3\pi }{2}\right)$ để:

a) Hàm số y = tanx nhận giá trị bằng ‒1;

b) Hàm số y = tanx nhận giá trị bằng 0;

c) Hàm số y = cotx nhận giá trị bằng 1;

d) Hàm số y = cotx nhận giá trị bằng 0.

Lời giải:

a) Xét đồ thị hàm số y = ‒1 và đồ thị hàm số y = tanx trên khoảng $\left(-\pi ;\frac{3\pi }{2}\right)$:

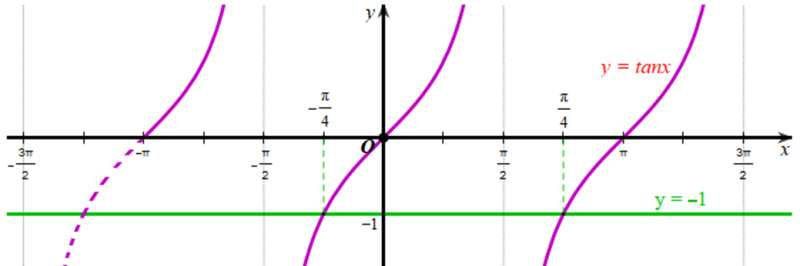
Quan sát đồ thị của hai hàm số, ta thấy hàm số y = tanx nhận giá trị bằng ‒1 tại x$\in \left(-\frac{\pi }{4};\frac{\pi }{4}\right)$.

b) Xét đồ thị hàm số y = tanx trên khoảng $\left(-\pi ;\frac{3\pi }{2}\right)$:

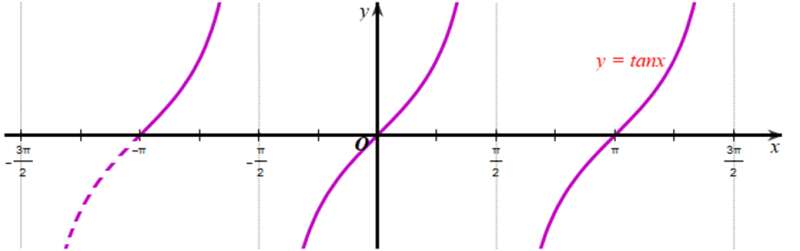
Quan sát hình vẽ, ta thấy hàm số y = tanx nhận giá trị bằng 0 tại x ∈ {0; π}.

c) Xét đồ thị hàm số y = 1 và đồ thị hàm số y = cotx trên khoảng $\left(-\pi ;\frac{3\pi }{2}\right)$:

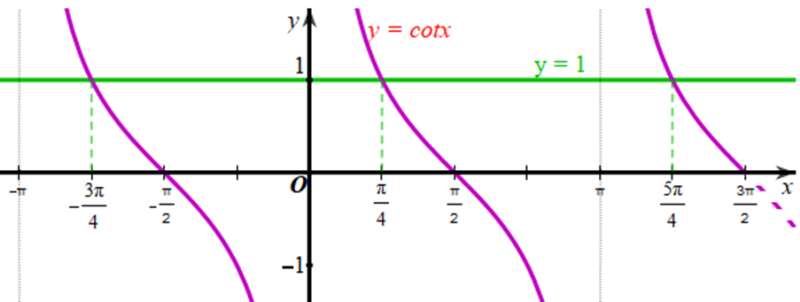
Quan sát đồ thị của hai hàm số, ta thấy hàm số y = cotx nhận giá trị bằng 1 tại x$\in \left(-\frac{3\pi }{4};\frac{\pi }{4};\frac{5\pi }{4}\right)$.

b) Xét đồ thị hàm số y = cotx trên khoảng $\left(-\pi ;\frac{3\pi }{2}\right)$:

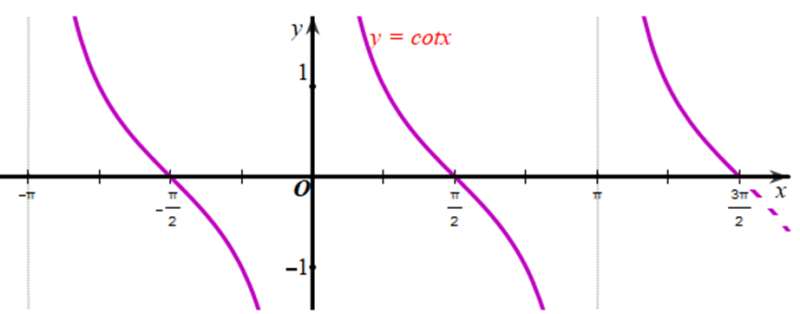
Quan sát hình vẽ, ta thấy hàm số y = cotx nhận giá trị bằng 0 tại x$\in \left(-\frac{\pi }{2};\frac{\pi }{2}\right)$.

Bài 3 trang 31 Toán 11 Tập 1: Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:

a) y = sinx trên khoảng $\left(-\frac{9\pi }{2};-\frac{7\pi }{2}\right),\left(\frac{21\pi }{2};\frac{23\pi }{2}\right)$;

b) y = cosx trên khoảng (‒20π; ‒19π), (‒9π; ‒8π).

Lời giải:

a) Xét hàm số y = sinx:

Do $\left(-\frac{9\pi }{2};-\frac{7\pi }{2}\right)=\left(-\frac{\pi }{2}-4\pi ;\frac{\pi }{2}-4\pi \right)$ nên hàm số y = sinx đồng biến trên khoảng $\left(-\frac{9\pi }{2};-\frac{7\pi }{2}\right)$.

Do $\left(\frac{21\pi }{2};\frac{23\pi }{2}\right)=\left(\frac{\pi }{2}+10\pi ;\frac{3\pi }{2}+10\pi \right)$ nên hàm số y = sinx nghịch biến trên khoảng $\left(\frac{21\pi }{2};\frac{23\pi }{2}\right)$.

b) Xét hàm số y = cosx:

Do (‒20π; ‒19π) = (0 ‒20π; π ‒ 20π) nên hàm số y = cosx nghịch biến trên khoảng (‒20π; ‒19π).

Do (‒9π; ‒8π) = (‒π – 8π; 0 ‒ 8π) nên hàm số y = cosx đồng biến trên khoảng (‒9π; ‒8π).

Bài 4 trang 31 Toán 11 Tập 1: Dùng đồ thị hàm số, hãy cho biết:

a) Với mỗi m ∈ [‒1;1], có bao nhiêu giá trị $\alpha \in \left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ sao cho sinα = m;

b) Với mỗi m ∈ [‒1;1], có bao nhiêu giá trị α ∈ [0; π] sao cho cosα = m;

c) Với mỗi m ∈ ℝ, có bao nhiêu giá trị $\alpha \in \left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ sao cho tanα = m;

d) Với mỗi m ∈ ℝ, có bao nhiêu giá trị α ∈ [0; π] sao cho cotα = m.

Lời giải:

a) Xét đồ thị hàm số y = m (m ∈ [‒1;1]) và đồ thị hàm số y = sinx trên :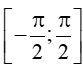

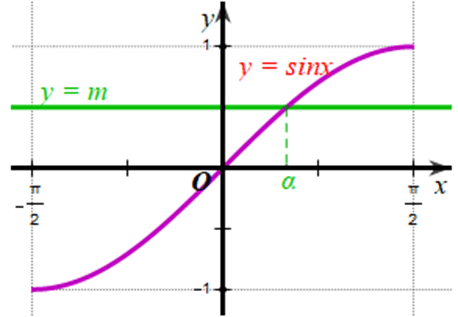
Từ đồ thị của hai hàm số ở hình vẽ trên, ta thấy với mỗi m ∈ [‒1;1] thì hai đồ thị cắt nhau tại 1 điểm.

Vậy với mỗi m ∈ [‒1;1] sẽ có 1 giá trị 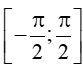$\alpha \in$  sao cho sinα = m.

b) Xét đồ thị hàm số y = m (m ∈ [‒1;1]) và đồ thị hàm số y = cosx trên [0; π]:

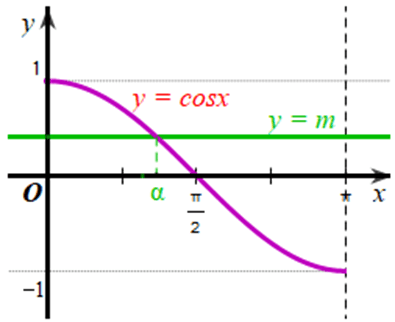
Từ đồ thị của hai hàm số ở hình vẽ trên, ta thấy với mỗi m ∈ [‒1;1] thì hai đồ thị cắt nhau tại 1 điểm.

Vậy m ∈ [‒1;1] sẽ có 1 giá trị α ∈ [0; π] sao cho cosα = m.

c) Xét đồ thị hàm số y = m (m ∈ ℝ) và đồ thị hàm số y = tanx trên :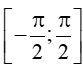

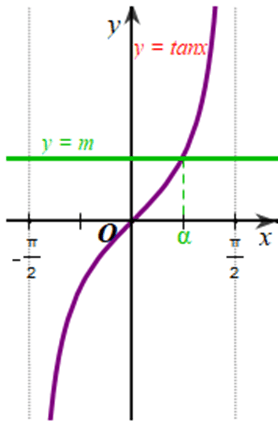
Từ đồ thị của hai hàm số ở hình vẽ trên, ta thấy với mỗi m ∈ ℝ thì hai đồ thị cắt nhau tại 1 điểm.

Vậy với mỗi m ∈ ℝ sẽ có 1 giá trị 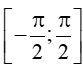$\alpha \in$  sao cho tanα = m.

d) Xét đồ thị hàm số y = m (m ∈ ℝ) và đồ thị hàm số y = cotx trên [0; π]:

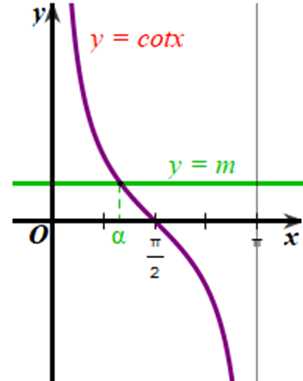
Từ đồ thị của hai hàm số ở hình vẽ trên, ta thấy với mỗi m ∈ ℝ thì hai đồ thị cắt nhau tại 1 điểm.

Vậy với mỗi m ∈ ℝ sẽ có 1 giá trị α ∈ [0; π] sao cho cotα = m.

Bài 5 trang 31 Toán 11 Tập 1: Xét tính chẵn, lẻ của các hàm số:

a) y = sinx cosx;

b) y = tanx + cotx;

c) y = sin²x.

Lời giải:

a) Xét hàm số f(x) = y = sinx cosx có D = ℝ:

• ∀x ∈ D thì ‒x ∈ D;

• f(‒x) = sin(‒x) . cos(‒x) = ‒sinx cosx = ‒f(x).

Do đó hàm số y = sinx cosx là hàm số lẻ.

b) Xét hàm số f(x) = y = tanx + cotx có D=R\$\left(k\pi ;\frac{\pi }{2}+k\pi |k\in \mathbb{Z}\right)$:

• ∀x ∈ D thì ‒x ∈ D;

• f(‒x) = tan(‒x) + cot(‒x) = (‒tanx) + (‒cotx) = ‒(tanx + cotx) = ‒f(x).

Do đó hàm số y = tanx + cotx là hàm số lẻ.

c) Xét hàm số f(x) = y = sin²x có D = ℝ:

• ∀x ∈ D thì ‒x ∈ D;

• f(‒x) = sin²(‒x) = (‒sinx)² = sin²x = f(x).

Do đó hàm số y = tanx + cotx là hàm số chẵn.

Bài 6 trang 31 Toán 11 Tập 1: Một dao động điều hoà có phương trình li độ dao động là: x = Acos(ωt + φ), trong đó t là thời gian tính bằng giây, A là biên độ dao động và x là li độ dao động đều được tính bằng centimét. Khi đó, chu kì T của dao động là T=$\frac{2\pi }{\omega }$. Xác định giá trị của li độ khi t = 0, $t=\frac{T}{4},t=\frac{T}{2},t=\frac{3T}{4}$, t = T và vẽ đồ thị biểu diễn li độ của dao động điều hoà trên đoạn [0; 2T] trong trường hợp:

a) A = 3 cm, φ = 0;

b) A = 3 cm, $\phi =-\frac{\pi }{2}$;

c) A = 3 cm, $\phi =\frac{\pi }{2}$.

Lời giải:

Từ T = $\frac{2\pi }{\omega }$ ta có $\omega =\frac{2\pi }{T}$.

Khi đó ta có phương trình li độ là x = Acos$\left(\frac{2\pi }{T}.t+\phi \right)$.

a)

‒ Với A = 3 cm và φ = 0 thay vào phương trình li độ x = Acos$\left(\frac{2\pi }{T}.t+\phi \right)$ ta có:

x = 3cos$\left(\frac{2\pi }{T}.t\right)$.

• t = 0 thì x = 3cos0 = 3;

• t = $\frac{T}{4}$ thì x = 3cos$\left(\frac{2\pi }{T}.\frac{T}{4}\right)$= 3cos$\frac{\pi }{2}$ = 0;

• t = $\frac{T}{2}$ thì x = 3cos$\left(\frac{2\pi }{T}.\frac{T}{2}\right)$ = 3cos$\pi$ = -3

• t = $\frac{3T}{4}$ thì x = 3cos$\left(\frac{2\pi }{T}.\frac{3T}{4}\right)$ = 3cos$\frac{3\pi }{2}$ = 0;

• t = T thì x = 3cos$\left(\frac{2\pi }{T}.T\right)$ = 3cos2$\pi$ = 3

‒ Vẽ đồ thị biểu diễn li độ của dao động điều hoà x = 3cos$\left(\frac{2\pi }{T}.t\right)$ trên đoạn [0; 2T]:

Xét hàm số x = 3cos$\left(\frac{2\pi }{T}.t\right)$ có chu kì là T.

Ta vẽ đồ thị hàm số x = 3cos$\left(\frac{2\pi }{T}.t\right)$ trên đoạn [0; T] theo bảng sau:

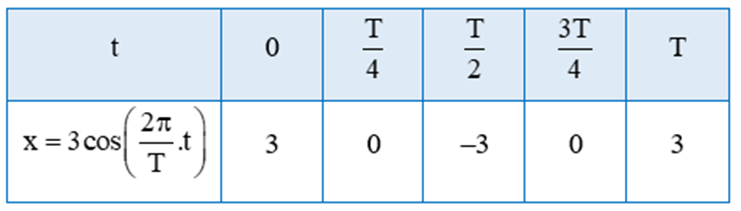
Bằng cách dịch chuyển đồ thị hàm số x = 3cos$\left(\frac{2\pi }{T}.t\right)$ trên đoạn [0; T] song song với trục hoành sang phải theo đoạn có độ dài T, ta sẽ nhận được đồ thị hàm số x = 3cos$\left(\frac{2\pi }{T}.t\right)$ trên đoạn [T; 2T].

Từ đó ta vẽ được đồ thị biểu diễn li độ của dao động điều hoà x = 3cos$\left(\frac{2\pi }{T}.t\right)$ trên đoạn [0; 2T] như sau:

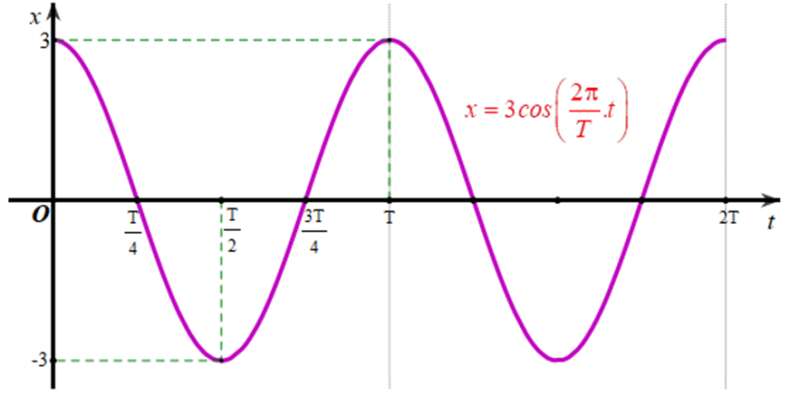
b)

‒ Với A = 3 cm và $\phi =-\frac{\pi }{2}$ thay vào phương trình li độ x = Acos$\left(\frac{2\pi }{T}.t+\phi \right)$ ta có:

x = 3cos$\left(\frac{2\pi }{T}.t-\frac{\pi }{2}\right)$ = 3cos$\left(\frac{\pi }{2}-\frac{2\pi }{T}.t\right)$ = 3sin$\left(\frac{2\pi }{T}.t\right)$

• t = 0 thì x = 3sin$\left(\frac{2\pi }{T}.0\right)$ = 3sin0 = 0

• t = $\frac{T}{4}$ thì x = 3sin$\left(\frac{2\pi }{T}.\frac{T}{4}\right)$ = 3sin$\frac{\pi }{2}$ = 3;

• t = $\frac{T}{2}$ thì x = 3sin$\left(\frac{2\pi }{T}.\frac{T}{2}\right)$ = 3sin$\pi$ = 0;

• t = $\frac{3T}{4}$ thì x = 3sin$\left(\frac{2\pi }{T}.\frac{3T}{4}\right)$ = 3sin$\frac{3\pi }{2}$ = -3;

• t = T thì x = 3sin$\left(\frac{2\pi }{T}.T\right)$ = 3sin2$\pi$ = 0.

‒ Vẽ đồ thị biểu diễn li độ của dao động điều hoà x = 3sin$\left(\frac{2\pi }{T}.t\right)$ trên đoạn [0; 2T]:

Xét hàm số x = 3sin$\left(\frac{2\pi }{T}.t\right)$ có chu kì là T.

Ta vẽ đồ thị hàm số x = 3sin$\left(\frac{2\pi }{T}.t\right)$ trên đoạn [0; T] theo bảng sau:

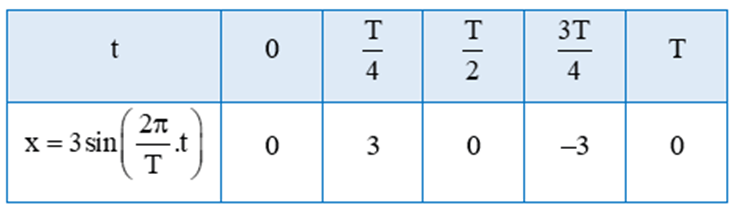
Bằng cách dịch chuyển đồ thị hàm số x = 3sin$\left(\frac{2\pi }{T}.t\right)$ trên đoạn [0; T] song song với trục hoành sang phải theo đoạn có độ dài T, ta sẽ nhận được đồ thị hàm số x = 3sin$\left(\frac{2\pi }{T}.t\right)$ trên đoạn [T; 2T].

Từ đó ta vẽ được đồ thị biểu diễn li độ của dao động điều hoà x = 3sin$\left(\frac{2\pi }{T}.t\right)$ trên đoạn [0; 2T] như sau:

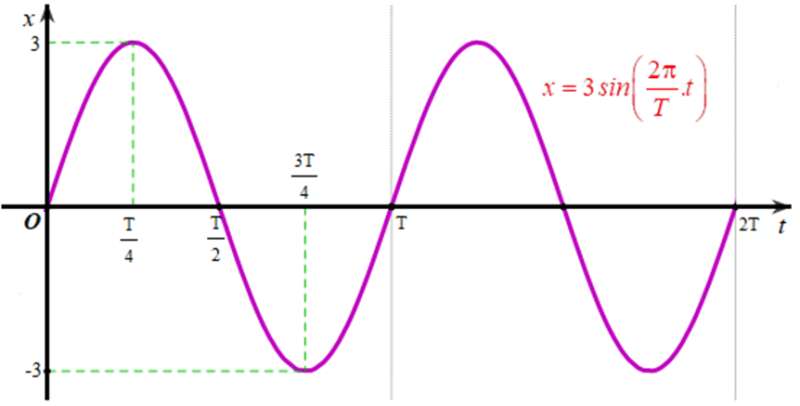
c)

‒ Với A = 3 cm và $\phi =\frac{\pi }{2}$ thay vào phương trình li độ x = Acos$\left(\frac{2\pi }{T}.t+\phi \right)$ ta có:

x = 3cos$\left(\frac{2\pi }{T}.t+\frac{\pi }{2}\right)$ = -3cos$\left(\pi -\left(\frac{2\pi }{T}.t+\frac{\pi }{2}\right)\right)$

= -3cos$\left(\frac{\pi }{2}-\frac{2\pi }{T}.t\right)$ = -3sin$\left(\frac{2\pi }{T}.t\right)$

• t = 0 thì x = -3sin$\left(\frac{2\pi }{T}.0\right)$ = -3sin0 = 0

• t = $\frac{T}{4}$ thì x = -3sin$\left(\frac{2\pi }{T}.\frac{T}{4}\right)$ = -3sin$\frac{\pi }{2}$ = -3;

• t = $\frac{T}{2}$ thì x = -3sin$\left(\frac{2\pi }{T}.\frac{T}{2}\right)$ = -3sin$\pi$ = 0;

• t = $\frac{3T}{4}$ thì x = -3sin$\left(\frac{2\pi }{T}.\frac{3T}{4}\right)$ = -3sin$\frac{3\pi }{2}$ = 3;

• t = T thì x = -3sin$\left(\frac{2\pi }{T}.T\right)$ = -3sin2$\pi$ = 0.

‒ Vẽ đồ thị biểu diễn li độ của dao động điều hoà x = -3sin$\left(\frac{2\pi }{T}.t\right)$ trên đoạn [0; 2T]:

Đồ thị hàm số x = -3sin$\left(\frac{2\pi }{T}.t\right)$ là hình đối xứng với đồ thị hàm số x = 3sin$\left(\frac{2\pi }{T}.t\right)$ qua trục hoành:

Bài 7 trang 31 Toán 11 Tập 1: Trong bài toán mở đầu, hãy chỉ ra một số giá trị của x để ống đựng nước cách mặt nước 2m

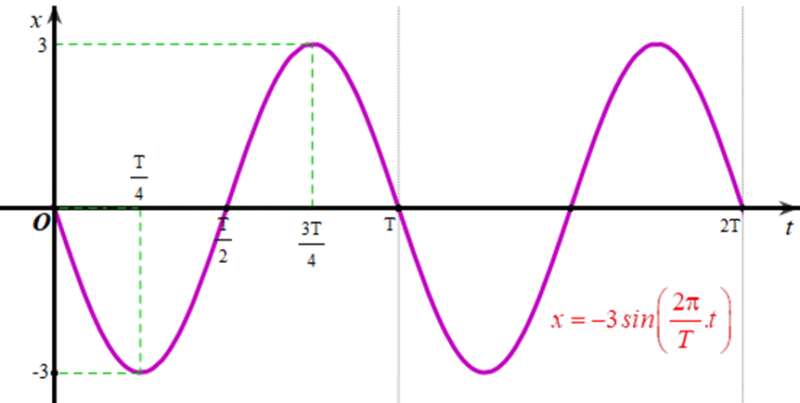
Lời giải:

Để ống đựng nước cách mặt nước 2m, ta có phương trình:

|2,5sin(2$\pi$x - $\frac{\pi }{2}$) + 2| = 2

TH1: 2,5sin(2x - $\frac{\pi }{2}$) + 2 = 2

$\iff$sin(2$\pi$x - $\frac{\pi }{2}$) = 0

$\Rightarrow$2$\pi$x - $\frac{\pi }{2}$ = k$\pi$

$\iff$x = $\frac{2k +1}{4}$

Vì x $\ge 0$ nên

Một số giá trị của x là: $\frac{1}{4}; \frac{5}{4}$

TH2:

$$\begin{gathered} 2,5.\sin \left(2\pi x-\frac{\pi }{2}\right)+2=-2 \\ \iff \sin \left(2\pi x-\frac{\pi }{2}\right)=-1,6<-1 \end{gathered}$$

Vì tập giá trị của hàm số sin là $\left[-1;1\right]$ nên trong trường hợp này phương trình vô nghiệm.

Vậy một số giá trị của x để ống nước cách mặt nước 2m là $\frac{1}{4};\frac{3}{4};\frac{5}{4}$

Xem thêm các bài giải sách giáo khoa Toán 11 Cánh Dều hay, chi tiết khác:

Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác

Bài 2: Các phép biến đổi lượng giác

Bài 4: Phương trình lượng giác cơ bản

Bài tập cuối chương 1

Bài 1: Dãy số