Toptailieu.vn giới thiệu Giải bài tập Toán lớp 7 Bài 6: Số vô tỉ. Căn bậc hai số học sách Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7 Tập 1. Mời các bạn đón xem:

Giải SGK Toán 7 Bài 6 (Kết nối tri thức): Số vô tỉ. Căn bậc hai số học

1. Số vô tỉ

Hoạt động 1 trang 29 Toán 7: Cắt một hình vuông cạnh bằng 2 dm, rồi cắt nó thành bốn tam giác vuông bằng nhau dọc theo hai đường chéo của hình vuông (H.2.2.a)

Phương pháp giải:

Cắt theo mô tả của đề bài

Lời giải:

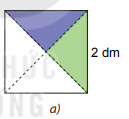
Bước 1: Cắt một hình vuông cạnh bằng 2 dm

Bước 2: Cắt hình vuông thành bốn tam giác vuông bằng nhau dọc theo hai đường chéo của hình vuông.

Hoạt động 2 trang 29 Toán 7: Lấy hai trong bốn tam giác nhận được ở trên ghép thành một hình vuông (H.2.2.b). Em hãy tính diện tích hình vuông nhận được.

Phương pháp giải:

Ghép 2 tam giác như hình.

Diện tích hình vuông = Diện tích hình vuông ban đầu (cạnh 2 dm) : 2

Lời giải:

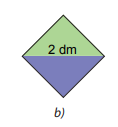
Lấy hai trong bốn tam giác nhận được ở trên ghép thành một hình vuông.

Vì 2 tam giác vuông chiếm một nửa hình vuông ban đầu nên

Diện tích hình vuông thu được là:

2.2:2= 2 (dm2)

Hoạt động 3 trang 29 Toán 7: Dùng thước có vạch chia để đo độ dài cạnh hình vuông nhận được trong HĐ2. Độ dài cạnh hình vuông này bằng bao nhiêu đềximét ?

Phương pháp giải:

Bước 1: Dùng thước đo cạnh hình vuông nhận được trong HĐ2, ta được số liệu có đơn vị cm.

Bước 2: Đổi đơn vị cm sang dm.

Lời giải:

Dùng thước đo ta được cạnh hình vuông dài khoảng 14 cm.

Ta có: 14 cm = 1,4 dm

Vận dụng trang 30 Toán 7: Người xưa đã tính đường kính thân cây theo quy tắc “quân bát, phát tam, tổn ngũ, quân nhị”, tức là lấy chu vi thân cây chia làm 8 phần bằng nhau (quân bát); bớt đi ba phần (phát tam) còn lại 5 phần (tổn ngũ) rồi chia đôi kết quả (quân nhị). Hãy cho biết người xưa đã ước lượng số $\pi$ bằng bao nhiêu?

Phương pháp giải:

Từ công thức tính chu vi đường tròn: C = $\pi$. d $a=\sqrt{S}$$\Rightarrow d=\frac{C}{\pi }$$$

Thực hiện theo quy tắc “quân bát, phát tam, tổn ngũ, quân nhị”

Lời giải:

Theo quy tắc “quân bát, phát tam, tổn ngũ, quân nhị”, có: $d=\frac{C}{8}.5:2=\frac{C}{8}.5.\frac{1}{2}=\frac{5C}{16}=\frac{C}{\frac{16}{5}}$

Theo công thức, có: $d=\frac{C}{\pi }$

Như vậy, người xưa đã ước lượng số $\pi$ bằng $\frac{16}{5}=3,2$.

2. Căn bậc hai số học

Luyện tập 1 trang 30 Toán 7:Tính: $a)\sqrt{16};b)\sqrt{81};c)\sqrt{{2021}^2}$

Phương pháp giải:

$\sqrt{a}=x$ thì ta có: $a=x^2(x\ge 0)$

Lời giải:

a) Vì $4^2=16$ nên $\sqrt{16}=4$

b) Vì $9^2=81$ nên $\sqrt{81}=9$

c) Vì 2021 > 0 nên $\sqrt{{2021}^2}=2021$

Vận dụng 1 trang 30 Toán 7: Sàn thi đấu bộ môn cử tạ có dạng một hình vuông, diện tích 144 m2. Em hãy tính chu vi của sàn thi đấu đó

Phương pháp giải:

Tìm cạnh a của hình vuông có diện tích S: $a=\sqrt{S}$

Tính chu vi hình vuông cạnh a là: C = 4.a

Lời giải:

Cạnh của sàn thi đấu là: $\sqrt{144}=12$ (m)

Chu vi của sàn thi đấu là: 4. 12 = 48 (m)

3. Tính căn bậc hai số học bằng máy tính cầm tay

Luyện tập 2 trang 31 Toán 7: Sử dụng máy tính cầm tay tính các căn bậc hai số học sau (làm tròn kết quả với độ chính xác 0,005, nếu cần).

$a)\sqrt{15};b)\sqrt{2,56};c)\sqrt{17256};d)\sqrt{793881}$

Phương pháp giải:

+ Bước 1: Bấm máy tính, tính các căn bậc hai.

+ Bước 2: Xác định hàng làm tròn.

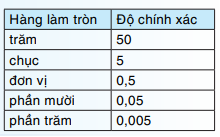
+ Bước 3: Làm tròn theo quy tắc làm tròn số thập phân.

- Đối với chữ số hàng làm tròn:

    + Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;

    +Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5

- Đối với chữ số sau hàng làm tròn:

    + Bỏ đi nếu ở phần thập phân;

    + Thay bằng các chữ số 0 nếu ở phần số nguyên

Lời giải:

Độ chính xác 0,005 tức là ta cần làm tròn đến hàng phần trăm

$\begin{array}{l}a)\sqrt{15}\approx 3,87\\ b)\sqrt{2,56}=1,6\\ c)\sqrt{17256}\approx 131,36\\ d)\sqrt{793881}=891\end{array}$

Vận dụng 2 trang 31 Toán 7: Kim tự tháp Kheops là công trình kiến trúc nổi tiếng thế giới. Để xây dựng được công trình này, người ta phải sử dụng tới hơn 2,5 triệu mét khối đá, với diện tích đáy lên tới 52 198,16 m2.Biết rằng đáy của kim tự tháp Kheops có dạng một hình vuông. Tính độ dài cạnh đáy của kim tự tháp này (làm tròn kết quả đến chữ số thập phân thứ nhất).

Phương pháp giải:

Tính cạnh a của hình vuông có diện tích S: $a=\sqrt{S}$

Làm tròn theo quy tắc làm tròn số thập phân.

- Đối với chữ số hàng làm tròn:

    + Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;

    +Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5

- Đối với chữ số sau hàng làm tròn:

    + Bỏ đi nếu ở phần thập phân;

    + Thay bằng các chữ số 0 nếu ở phần số nguyên

Lời giải:

Độ dài cạnh đáy của kim tự tháp này là: $\sqrt{52198,16}\approx 228,469$(m)

Làm tròn đến chữ số thập phân thứ nhất, ta được: 228,5 m.

Bài tập

Bài 2.6 trang 32 Toán 7: Cho biết ${153}^2=23409$. Hãy tính $\sqrt{23409}$

Phương pháp giải:

  x^2=a thì √a=x (x > 0)

Lời giải:

$\sqrt{23409}$ = 153.

Bài 2.7 trang 32 Toán 7: Từ các số là bình phương cảu 12 số tự nhiên đầu tiên, em hãy tìm căn bậc hai số học của các số sau:

a) 9;                                        b) 16;

c) 81;                                      d) 121

Phương pháp giải

x^2=a thì √a=x (x>0)

Lời giải:

a) Vì $3^2=9$ nên $\sqrt{9}=3$

b) Vì $4^2=16$ nên $\sqrt{16}=4$

c) Vì $9^2=81$ nên $\sqrt{81}=9$

d) Vì ${11}^2=121$ nên $\sqrt{121}=11$

Bài 2.8 trang 32 Toán 7: Khi tìm căn bậc hai số học của một số tự nhiên ta thường phân tích số đó ra thừa số nguyên tố. Chẳng hạn:

Vì $324=2^2{.3}^4=({2.3}^2{)}^2={18}^2$ nên $\sqrt{324}=18$

Tính căn bậc hai số học của 129 600.

Phương pháp giải

Phân tích 129 600 ra thừa số nguyên tố, rồi đưa về dạng 

Lời giải

Ta có: $129600=2^6{.3}^4{.5}^2=(2^3{.3}^2.5{)}^2={360}^2$ nên $\sqrt{129600}=360$

Bài 2.9 trang 32 Toán 7: Tính độ dài các cạnh của hình vuông có diện tích bằng:

a) 81 dm2;       b) 3 600 m2;                c) 1 ha

Phương pháp giải

Tìm căn bậc hai số học của một số.

Chú ý đơn vị.

Lời giải:

a) Độ dài các cạnh của hình vuông là: $\sqrt{81}=9$ (dm)

b) Độ dài các cạnh của hình vuông là: $\sqrt{3600}=60$ (m)

c) Đổi 1 ha  = 10 000 m2

Độ dài các cạnh của hình vuông là: $\sqrt{10000}=100$ (m)

Chú ý: Câu c cần đổi đơn vị trước khi tìm căn bậc hai số học.

Bài 2.10 trang 32 Toán 7: Sử dụng máy tính cầm tay tìm căn bậc hai số học của các số sau rồi làm tròn các kết quả với độ chính xác 0,005.

a) 3;                                        b) 41;                                 c) 2 021

Phương pháp giải

* Bấm máy tính tìm căn bậc hai số học.

* Làm tròn theo quy tắc làm tròn số thập phân.

- Đối với chữ số hàng làm tròn:

    + Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;

    +Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5

- Đối với chữ số sau hàng làm tròn:

    + Bỏ đi nếu ở phần thập phân;

    + Thay bằng các chữ số 0 nếu ở phần số nguyên

Lời giải:

Làm tròn các kết quả với độ chính xác 0,005 tức là làm tròn đến hàng phần trăm.

$\begin{array}{l}a)\sqrt{3}=1,\mathrm{73205....}\approx 1,73\\ b)\sqrt{41}=6,\mathrm{40312....}\approx 6,40\\ c)\sqrt{2021}=44,\mathrm{95553....}\approx 44,96\end{array}$

Bài 2.11 trang 32 Toán 7: Biết rằng bình phương độ dài đường chéo của một hình chữ nhật bằng tổng các bình phương độ dài hai cạnh của nó. Một hình chữ nhật có chiều dài là 8 dm và chiều rộng là 5 dm. Độ dài đường chéo của hình chữ nhật đó bằng bao nhiêu đềximét (làm tròn kết quả đến hàng phần mười)?

Phương pháp giải

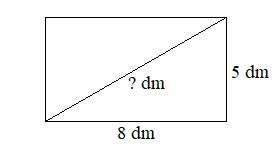
Bước 1: Tính tổng các bình phương độ dài hai cạnh của hình chữ nhật.

Bước 2: Tìm căn bậc hai số học của tổng vừa tìm được bằng máy tính cầm tay

Bước 3: Làm tròn kết quả đến hàng phần mười.

Lời giải:

Ta có: Bình phương độ dài đường chéo của một hình chữ nhật là: $5^2+8^2=25+64=89$

Độ dài đường chéo của một hình chữ nhật là: $\sqrt{89}=9,\mathrm{43398...}$(dm)

Làm tròn kết quả này ta được: 9,4 dm

Chú ý: Độ dài đường chéo của một hình chữ nhật bằng căn bậc hai số học của tổng các bình phương độ dài hai cạnh của nó

Bài 2.12 trang 32 Toán 7: Để lát một mảnh sân hình vuông có diện tích 100 m2, người ta cần dùng bao nhiêu viên gạch hình vuông có cạnh dài 50 cm (coi các mạch ghép là không đáng kể)?

Phương pháp giải

Bước 1: Tìm diện tích 1 viên gạch

Bước 2: Đổi các số liệu về cùng đơn vị

Bước 3: Tìm số viên gạch

Lời giải:

Diện tích 1 viên gạch là: 502 = 2500 (cm2) = 0,25 m2.

Số viên gạch cần là: 100 : 0,25 = 400 (viên)