Toptailieu.vn giới thiệu Giải bài tập Toán lớp 6 trang 9, 10, 11, 12 Bài 2: Cách ghi số tự nhiên sách Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6 Tập 1. Mời các bạn đón xem:

Toán 6 (Kết nối tri thức) trang 9, 10, 11, 12 Bài 2: Cách ghi số tự nhiên

Trả lời câu hỏi giữa bài

Toán lớp 6 trang 9 Câu hỏi: Từ ba chữ số 0, 1 và 2, viết các số tự nhiên có ba chữ số, mỗi chữ số chỉ viết một lần.

Phương pháp giải: 

+ Bước 1: Chọn chữ số hàng trăm ( khác 0)

+ Bước 2: Chọn chữ số hàng chục ( khác chữ số hàng trăm)

+ Bước 3: Chọn chữ số hàng đơn vị ( khác chữ số hàng trăm, hàng chục)

Lời giải:

Các số có ba chữ số lập được là: 120, 210, 102, 201

Toán lớp 6 trang 10 Hoạt động: Trong số 32 019, ta thấy:

"Chữ số 2 nằm ở hàng nghìn và có giá trị bằng 2 x 1 000 = 2 000".

Hãy phát biểu theo mẫu câu đó đối với các chữ số còn lại.

Phương pháp giải: 

- Chữ số hàng chục nghìn có giá trị bằng số đó nhân với 10000

- Chữ số hàng trăm có giá trị bằng số đó nhân với 100

- Chữ số hàng chục có giá trị bằng số đó nhân với 10.

- Chữ số hàng đơn vị có giá trị bằng số đó.

Lời giải:

- Chữ số 3 nằm ở hàng chục nghìn có giá trị bằng 3 x 10 000 = 30 000

- Chữ số 0 nằm ở hàng trăm có giá trị bằng 0 x 100 = 0

- Chữ số 1 nằm ở hàng chục có giá trị bằng 1 x 10 = 10

- Chữ số 9 nằm ở hàng đơn vị có giá trị bằng 9.

Toán lớp 6 trang 10 Hoạt động: Viết số 32 019 thành tổng giá trị các chữ số của nó. 

Phương pháp giải: 

Cộng các giá trị của các hàng đã tính ở HĐ1

Lời giải:

32 019 = 3 x 10 000 + 2 x 1 000 + 0 x 100 + 1 x 10 + 9 x 1

Toán lớp 6 trang 10 Luyện tập: Viết số 34 604 thành tổng giá trị các chữ số của nó

Lời giải:

Số 34 604 được viết thành tổng giá trị các chữ số của nó là:

34 604 = (3 x 10 000) + (4 x 1 000) + (6 x 100) + (0 x 10) + 4

Toán lớp 6 trang 10 Vận dụng: Bác Hoa đi chợ, Bác chi mang ba loại tiền: loại (có mệnh giá) 1 nghìn (1 0000 đồng, loại 10 nghìn (10 000 đồng và loại 100 nghìn (100 000 đồng. Tổng số tiền bác phải trả là 492 nghìn đồng. Nếu mỗi loại tiền, bác mang theo không quá 9 tờ thì bác sẽ phải trả bao nhiêu tờ tiền mỗi loại, mà người bán không phải trả lại tiền thừa?

Phương pháp giải: 

Viết số 492 thành tổng giá trị các chữ số của nó từ đó suy ra số tờ tiền mỗi loại phải trả.

Lời giải:

Ta biểu diễn 492 thành:

492 = (4 x 100) + (9 x 10) + 2 x 1

Vậy để người bán hàng không phải trả lại tiền thừa thì số tờ tiền mỗi loại bác phải trả là: 4 tờ loại

100 nghìn (100 000) đồng, 9 tờ 10 nghìn (10 000 đồng) và 2 tờ loại 1 nghìn (1 000 đồng)

Toán lớp 6 trang 11 Câu hỏi: a) Viết các số 14 và 27 bằng số La Mã.

b) Đọc các số La Mã XVI, XXII.

Phương pháp giải: 

Xem cách viết số La Mã SGK (Trang 11)

Lời giải:

a) Số 14: XIV

Số 27: XXVII

b) XVI: Mười sáu

XXII: Hai mươi hai

Toán lớp 6 trang 11 Thử thách nhỏ: Sử dụng đúng 7 que tính, em xếp được những số La Mã nào?

Phương pháp giải: 

Ghép các que tính thành các số La Mã

Lời giải:

Các số có thể ghép được: XVIII (18), XXIII (23), XXIV (24), XXVI (26), XXIX(29), XXXI(31).

Bài tập trang 12

Toán lớp 6 trang 12 Bài 1.6: Cho các số: 27 501; 106 712; 7 110 385; 2 915 404 267 (viết trong hệ thập phân)

a) Đọc mỗi số đã cho

b) Chữ số 7 trong mỗi số đã cho có giá trị bằng bao nhiêu

Phương pháp giải: 

a) Đọc các số đã cho

b) Số 7 đứng ở hàng nào thì nhân 7 với số tương ứng.

Lời giải:

a)

27 501: Hai mươi bảy nghìn năm trăm lẻ một

106 712: Một trăm lẻ sáu nghìn bảy trăm mười hai

7 110 385: Bảy triệu một trăm mười nghìn ba trăm tám mươi lăm

2 915 404 267: Hai tỉ chín trăm mười lăm triệu bốn trăm lẻ bốn nghìn hai trăm sáu mươi bảy.

b)

27 501: chữ số 7 nằm ở hàng nghìn và có giá trị là 7x1 000 = 7 000

106 712: chữ số 7 nằm ở hàng trăm và có giá trị là 7x 100 = 700

7 110 385: chữ số 7 nằm ở hàng triệu và có giá trị là 7x 1 000 000 = 7 000 000

2 915 404 267: chữ số 7 nằm ở hàng đơn vị và có giá trị là 7x1 = 7

Toán lớp 6 trang 12 Bài 1.7: Chữ số 4 đứng ở hàng nào trong một số tự nhiên nếu nó có giá trị bằng

a) 400

b) 40

c) 4

Phương pháp giải: 

Đếm số chữ số 0 sau số 4, nếu không có số 0 thì 4 đứng ở hàng đơn vị, có 1 số 0 thì 4 đứng ở hàng chục, có hai số 0 thì 4 đứng ở hàng trăm.

Lời giải:

a) Vì 400 = 4 x 100 nên chữ số 4 có giá trị bằng 400 khi nó đứng ở hàng trăm.

b) Vì 40 = 4 x 10 nên chữ số 4 có giá trị bằng 40 khi nó đứng ở hàng chục.

c) Vì 4 = 4 x 1 nên chữ số 4 có giá trị bằng 4 khi nó đứng ở hàng đơn vị.

Toán lớp 6 trang 12 Bài 1.8: Đọc các số La Mã XIV; XVI; XXIII.

Phương pháp giải: 

Đọc các số La Mã đã cho

Lời giải:

XIV : mười bốn

XVI : mười sáu

XXIII: hai mươi ba

Toán lớp 6 trang 12 Bài 1.9: Viết các số sau bằng số La Mã: 18, 25

Phương pháp giải: 

Viết các số đã cho bằng số La Mã

Lời giải:

18: XVIII

25: XXV

Toán lớp 6 trang 12 Bài 1.10: Một số tự nhiên được viết bởi ba chữ số 0 và ba chữ số 9 nằm xen kẽ nhau. Đó là số nào?

Phương pháp giải: 

Do số 0 không thể đứng đầu tiên từ trái qua phải nên ta viết số 9 đứng đầu su đó viết các số xen kẽ nhau

Lời giải:

Vì số 0 không thể đứng đầu nên số cần tìm là 909 090.

Toán lớp 6 trang 12 Bài 1.11: Dùng các chữ số 0, 3 và 5, viết một số tự nhiên có ba chữ số khác nhau mà chữ số 5 có giá trị là

50

Phương pháp giải: 

Lưu ý chữ số 0 không thể đứng ở hàng trăm

Lời giải:

Chữ số 5 có giá trị là 50 nên nó ở hàng chục.

Số 0 không thể đứng đầu nên chữ số 3 ở hàng trăm và chữ số 0 ở hàng đơn vị.

Vậy số cần tìm là 350.

Toán lớp 6 trang 12 Bài 1.12: Trong một cửa hàng bánh kẹo, người ta đóng gói kẹo thành các loại: mỗi gói có 10 cái kẹo, mỗi hộp có 10 gói, mỗi thùng có 10 hộp. Một người mua 9 thùng, 9 hộp và 9 gói kẹo. Hỏi người đó đã mua tất cả bao nhiêu cái kẹo

Phương pháp giải: 

Tính số cái kẹo có trong 1 hộp

Tính số cái kẹo có trong 1 thùng

=> Tính số kẹo trong 9 thùng, 9 hộp và 9 gói kẹo.

Lời giải:

Số cái kẹo có trong 1 hộp là: 10 x 10 = 100 (cái kẹo)

Số cái kẹo có trong 1 thùng là: 100 x 10 = 1 000 (cái kẹo)

Vậy một người mua 9 thùng, 9 hộp và 9 gói kẹo thì số kẹo người đó đã mua tất cả là:

      9 x 1000 + 9 x 100 + 9 x 10 = 9990 (cái kẹo)

Đáp số 9990 cái kẹo.

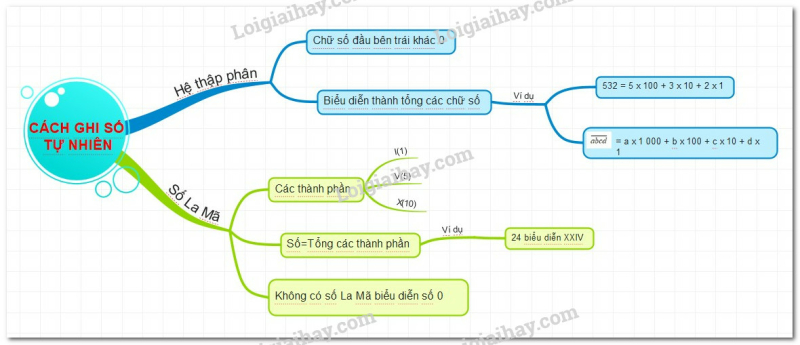
Lý thuyết Bài 2: Cách ghi số tự nhiên 

Biểu diễn 1 số dưới dạng tổng các chữ số của nó

I. Hệ thập phân

1. Cách ghi số tự nhiên trong hệ thập phân

Để ghi số tự nhiên trong hệ thập phân, người ta dùng mười chữ số là $0;1;2;3;4;5;6;7;8;9.$ Người ta lấy các chữ số trong 10 chữ số này rồi viết liền nhau thành một dãy, vị trí của các chữ số đó trong dãy gọi là hàng.

Trong hệ thập phân, cứ 10 đơn vị của một hàng thì làm thành 1 đơn vị của hàng liền trước đó. Ví dụ 10 chục thì bằng 1 trăm; mười trăm thì bằng 1 nghìn;...

Chú ý: Khi viết các số tự nhiên, ta quy ước:

1. Với các số tự nhiên khác 0, chữ số đầu tiên bên trái khác 0.

2. Đối với các số có 4 chữ số khác 0 trở lên, ta viết tách riêng từng lớp. Mỗi lớp là một nhóm 3 chữ só từ phải sang trái.

3. Với những số tự nhiên có nhiều chữ số, mỗi chữ số ở các vị trí (hàng) khác nhau thì có giá trị khác nhau

Ví dụ:

Số 120 250 160 555

- Đọc: Một trăm hai mươi tỉ, hai trăm năm mươi triệu một trăm sáu mươi nghìn năm trăm năm mươi lăm.

- Các lớp: lớp tỉ, triệu, nghìn, đơn vị được ghi lại như sau:

Lớp

Tỉ

Triệu

Nghìn

Đơn vị

Hàng

Trăm tỉ

Chục tỉ

Tỉ

Trăm triệu

Chục triệu

Triệu

Trăm nghìn

Chục nghìn

Nghìn

Trăm

Chục

Đơn vị

Chữ số

1

2

0

2

5

0

1

6

0

5

5

5

- Cùng là số 2 nhưng số 2 ở hàng chục tỉ có giá trị khác với số 2 ở hàng trăm triệu.

2. Cấu tạo thập phân của một số

+ Kí hiệu $\overline{ab}$ chỉ số tự nhiên có hai chữ số, chữ số hàng chục là $a\left(a\ne 0\right)$, chứ số hàng đơn vị là $b$. Ta có:

$\overline{ab}=\left(a\times 10\right)+b$với $a\ne 0.$

 

+ Kí hiệu $\overline{abc}$ chỉ số tự nhiên có 3 chữ số, chữ số hàng trăm là $a\left(a\ne 0\right)$,  chữ số hàng chục là $b$, chữ số hàng đơn vị là $c$. Ta có:

$\overline{abc}=a.100+b.10+c$ với $a\ne 0.$

+ Với các số tự nhiên cụ thể thì không có dấu gạch ngang trên đầu.

Ví dụ:

$\begin{array}{l}\overline{2b}=2.10+b\\ \overline{a5b}=a.100+5.10+b\left(a\ne 0\right)\end{array}$

$\overline{a03bcd}=a.100000+0.10000$$+3.1000+b.100+c.10+d$$\left(a\ne 0\right)$

II. Hệ La Mã

Cách viết số La Mã: Ta chỉ viết các số La Mã không quá 30.

+ Các thành phần để ghi số La Mã:

- Các kí tự  I, V, X : Các chữ số La Mã.

- Các cụm chữ số IV, IX

- Giá trị của các thành phần này không thay đổi dù ở vị trí nào.

Thành phần	I	V	X	IV	IX
Giá trị (viết trong hệ thập phân)	1	5	10	4	9

 

 

Các số La Mã biểu diễn các số từ 1 đến 10

I	II	III	IV	V	VI	VII	VIII	IX	X
1	2	3	4	5	6	7	8	9	10

 

Các số La Mã biểu diễn các số từ 11 đến 20: Thêm X vào bên trái mỗi số từ I đến X

XI	XII	XIII	XIV	XV	XVI	XVII	XVIII	XIX	XX
1	2	3	4	5	6	7	8	9	10

 

Các số La Mã biểu diễn các số từ 21 đến 30: Thêm XX vào bên trái mỗi số từ I đến X

XXI	XXII	XXIII	XXIV	XXV	XXVI	XXVII	XXVIII	XXIX	XXX
1	2	3	4	5	6	7	8	9	10

 

Chú ý:

- Mỗi số La Mã biểu diễn một số tự nhiên bằng tổng giá trị của các thành phần tạo nên số đó.

- Không có số La Mã nào biểu diễn số 0.

Ví dụ:

Số XIII có 4 thành phần là X, I, I, I tương ứng với các giá trị 10,1,1,1. Do đó biểu diễn số 10+1+1+1=13.

Viết số 17 thành số La Mã:

Số 7 được viết là VII

Số 17 = 7+10, tức là số 7 thêm 10 đơn vị nên ta thêm chữ X trước VII được: XVII

Các dạng toán về ghi số tự nhiên

1. Viết tất cả các số có n chữ số từ n chữ số cho trước

Phương pháp:

Giả sử từ ba chữ số  khác   ta viết các số có ba chữ số như sau:

Chọn  là chữ số hàng trăm ta có: , ;

Chọn  là chữ số hàng trăm ta có: , ;

Chọn  là chữ số hàng trăm ta có: , .

Vậy tất cả có 6 số có ba chữ số lập được từ ba chữ số khác :  và 

Chữ số  không thể đứng ở hàng cao nhất của số có   chữ số phải viết.

Dùng  chữ số , hãy viết tất cả các số có  chữ số mà các chữ số khác nhau.

Giải:

Chữ số hàng chục có thể là  hoặc .

Nếu chữ số hàng chục là  thì chữ số hàng đơn vị là .

Nếu chữ số hàng chục là  thì chữ số hàng đơn vị là .

2. Tính số các số có n chữ số cho trước

Phương pháp:

Bước 1: Tìm số nhỏ nhất và số lớn nhất có  chữ số.

Bước 2: Để tính số các số có   chữ số ta lấy số lớn nhất có   chữ số trừ đi số nhỏ nhất có  chữ số rồi cộng với 

Ví dụ:

Có bao nhiêu số có  chữ số?
Giải:
Số lớn nhất có  chữ số là .
Số nhỏ nhất có  chữ số là: .
Số các số có  chữ số là .

3. Sử dụng công thức đếm số các số tự nhiên

Phương pháp:

 Để đếm các số tự nhiên từ  đến   hai số liên tiếp cách nhau   đơn vị, ta dùng công thức sau:

 hay bằng (số cuối – số đầu):khoảng cách +1.

- Căn cứ vào các phần tử đã được liệt kê hoặc căn cứ vào tính chất đặc trưng cho các phần tử của tập hợp cho trước, ta có thể tìm được số phần tử của tập hợp đó.

- Sử dụng các công thức sau:

+ Tập hợp các số tự nhiên từ  đến  có:  phần tử  (1)

+ Tập hợp các số chẵn từ số chẵn  đến số chẵn  có:  phần tử  ( 2)

+ Tập hợp các số lẻ từ số lẻ  đến số lẻ  có:  phần tử  ( 3)

+ Tập hợp các số tự nhiên từ   đến   hai số kế tiếp cách nhau d đơn vị, có:  phần tử  (4)