Với giải Bài 7.44 trang 46 Toán lớp 7 SGK Tập 2 Kết nối tri thức chi tiết trong Bài tập cuối chương VII giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:

Giải bài tập Toán 7 Bài 7.44 trang 46 Toán lớp 7 SGK Tập 2

Bài 7.44 trang 46 Toán lớp 7 SGK Tập 2: Cho đa thức A = x⁴ + x³ – 2x – 2

a) Tìm đa thức B sao cho A + B = x³ + 3x + 1

b) Tìm đa thức C sao cho A – C = x⁵

c) Tìm đa thức D biết rằng D = (2x³ – 3) . A

d) Tìm đa thức P sao cho A = (x+1) . P

e) Có hay không một đa thức Q sao cho A = (x² + 1) . Q?

Phương pháp giải:

* Cách cộng (trừ) 2 đa thức:

Cách 1: Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.

Cách 2: Đặt tính cộng (trừ) sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng ( trừ) theo từng cột.

* Cách nhân 2 đa thức:

Cách 1: Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau

Cách 2: Đặt tính nhân:

+ Nhân lần lượt mỗi hạng tử ở dòng dưới với đa thức ở dòng trên và viết kết quả trng một dòng riêng.

+ Viết các dòng sao cho các hạng tử cùng bậc thẳng cột với nhau để thực hiện phép cộng theo cột.

*  Muốn chia đa thức A cho đa thức B, ta làm như sau:

Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B.

Bước 2: Lấy A trừ đi tích của B với thương mới thu được ở bước 1

Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B

Bước 4: Lấy dư thứ nhất trừ đi tích B với thương vừa thu được ở bước 3

Bước 5: Làm tương tự như trên

Đến khi dư cuối cùng có bậc nhỏ hơn bậc của B thì quá trình chia kết thúc.

Lời giải:

a) Ta có:

B = (A + B) – A

= (x³ + 3x + 1) – (x⁴ + x³ – 2x – 2)

= x³ + 3x + 1 – x⁴ - x³ + 2x + 2

= – x⁴ + (x³ – x³) + (3x + 2x) + (1 + 2)

= – x⁴ + 5x + 3

b) C = (A – C) – A

= x⁵ – (x⁴ + x³ – 2x – 2)

= x⁵ – x⁴ -  x³ + 2x + 2)

c) D = (2x³ – 3) . A

= (2x³ – 3) . (x⁴ + x³ – 2x – 2)

= 2x³ . (x⁴ + x³ – 2x – 2) + (-3) .(x⁴ + x³ – 2x – 2)

= 2x³ . x⁴ + 2x³ . x³ + 2x³ . (-2x) + 2x³ . (-2) + (-3). x⁴ + (-3) . x³ + (-3). (-2x) + (-3). (-2)

= 2x⁷ + 2x⁶ – 4x⁴ – 4x³ – 3x⁴ – 3x³ + 6x + 6

= 2x⁷ + 2x⁶ + (-4x⁴ – 3x⁴) + (-4x³ – 3x³) + 6x + 6

= 2x⁷ + 2x⁶ – 7x⁴ – 7x³ + 6x + 6

d) P = A : (x+1) = (x⁴ + x³ – 2x – 2) : (x + 1)

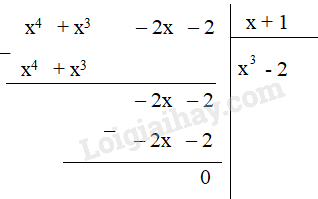
Vậy P = x³ - 2

e) Q = A : (x² + 1)

Nếu A chia cho đa thức x² + 1 không dư thì có một đa thức Q thỏa mãn

Ta thực hiện phép chia (x⁴ + x³ – 2x – 2) : (x² + 1)

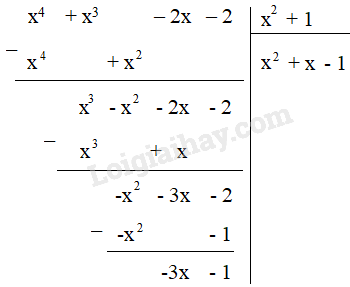
Do phép chia có dư nên không tồn tại đa thức Q thỏa mãn

Xem thêm các bài giải Toán 10 Kết nối tri thức hay, chi tiết khác:

Bài 7.42 trang 46 Toán lớp 7 SGK Tập 2: Một hãng taxi quy định giá cước như sau: 0,5 km đầu tiên giá 8 000 đồng; tiếp theo cứ mỗi kilomet giá 11 000 đồng. Giả sử một người thuê xe đi x (km)

Bài 7.43 trang 46 Toán lớp 7 SGK Tập 2: Cho đa thức bậc hai F(x) = ax² + bx + c, trong đó, a,b và c là những số với a ≠ 0

Bài 7.45 trang 46 Toán lớp 7 SGK Tập 2: Cho đa thức P(x). Giải thích tại sao nếu có đa thức Q(x) sao cho P(x) = (x – 3) . Q(x) (tức là P(x) chia hết cho x – 3) thì x = 3 là một nghiệm của P(x)

Bài 7.46 trang 46 Toán lớp 7 SGK Tập 2: Hai bạn Tròn và Vuông tranh luận với nhau như sau: