Toptailieu.vn giới thiệu Giải bài tập Toán lớp 7 trang 39, 40, 41, 42, 43 Bài 28: Phép chia đa thức một biến sách Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7 Tập 2. Mời các bạn đón xem:
Nội dung bài viết
Giải Toán lớp 7 trang 39, 40, 41, 42, 43 Bài 28: Phép chia đa thức một biến
1. Làm quen với phép chia đa thức
Hoạt động 1 trang 40 Toán lớp 7 SGK Tập 2: Tìm thương của mỗi phép chia sau:
a) 12x3 : 4x
b) (-2x4 ) : x4
c) 2x5 : 5x2
Phương pháp giải:
Bước 1: Chia 2 hệ số
Bước 2: Chia 2 lũy thừa của biến
Bước 3: Nhân 2 kết quả trên, ta được thương
Lời giải:
a) 12x3 : 4x = (12:4) . (x3 : x) = 3.x2
b) (-2x4 ) : x4 = [(-2) : 1] . (x4 : x4) = -2
c) 2x5 : 5x2 = (2:5) . (x5 : x2) = x3
Hoạt động 2 trang 40 Toán lớp 7 SGK Tập 2: Giả sử x 0. Hãy cho biết:
a) Với điều kiện nào ( của hai số mũ) thì thương hai lũy thừa của x cũng là một lũy thừa của x với số mũ nguyên dương?
b) Thương hai lũy thừa của x cùng bậc bằng bao nhiêu?
Phương pháp giải:
Lời giải:
a) Do nên muốn thương hai lũy thừa của x cũng là một lũy thừa của x với số mũ nguyên dương, tức là m – n > 0 thì m > n
b) Ta có:
Vậy thương hai lũy thừa của x cùng bậc bằng 1
Luyện tập 1 trang 40 Toán lớp 7 SGK Tập 2: Thực hiện các phép chia sau:
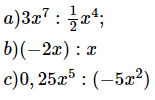
Phương pháp giải:
Bước 1: Chia 2 hệ số
Bước 2: Chia 2 lũy thừa của biến
Bước 3: Nhân 2 kết quả trên, ta được thương
Lời giải:
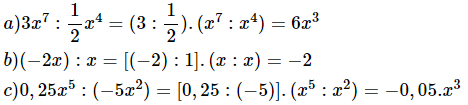
2. Chia đa thức cho đa thức, trường hợp chia hết
Phương pháp giải:
Nhân đa thức B với đa thức 2x2 – 5x + 1. Nếu kết quả bằng đa thức A thì đúng
Lời giải:
Ta có: B . (2x2 – 5x + 1)
= (x2 – 4x – 3) . (2x2 – 5x + 1)
= x2 .(2x2 – 5x + 1) – 4x . (2x2 – 5x + 1) – 3.(2x2 – 5x + 1)
= x2 . 2x2 + x2 . (-5x) + x2 . 1 – [4x . 2x2 + 4x . (-5x) + 4x . 1] – [3.2x2 + 3.(-5x) + 3.1]
= 2x4 – 5x3 + x2 – ( 8x3 – 20x2 + 4x) – (6x2 – 15x + 3)
= 2x4 – 5x3 + x2 – 8x3 + 20x2 - 4x – 6x2 + 15x - 3
= 2x4 + (-5x3 – 8x3) + (x2 + 20x2 – 6x2 ) + (-4x + 15x) – 3
= 2x4 - 13x3 + 15x2 + 11x - 3
=A
Vậy ta có phép chia hết A : B = 2x2 – 5x + 1
Luyện tập 2 trang 41 Toán lớp 7 SGK Tập 2: Thực hiện phép chia:
a) (-x6 + 5x4 – 2x3) : (0,5x2)
b) (9x2 – 4) : (3x + 2)
Phương pháp giải:
Muốn chia đa thức A cho đa thức B, ta làm như sau:
Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B.
Bước 2: Lấy A trừ đi tích của B với thương mới thu được ở bước 1
Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B
Bước 4: Lấy dư thứ nhất trừ đi tích B với thương vừa thu được ở bước 3
Bước 5: Làm tương tự như trên
Đến khi dư cuối cùng có bậc nhỏ hơn bậc của B thì quá trình chia kết thúc.
Lời giải:
a) (-x6 + 5x4 – 2x3) : (0,5x2)
= (-x6 : 0,5x2) + (5x4 : 0,5x2) + (-2x3 : 0,5x2)
= -2x4 + 10x2 – 4x
b)
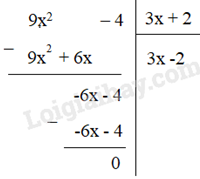
Vận dụng trang 41 Toán lớp 7 SGK Tập 2: Vận dụng giải bài toán tròn tính huống mở đầu
Tìm đa thức P sao cho A = B. P, trong đó A = 2x4 – 3x3 – 3x2 + 6x – 2 và B = x2 – 2
Phương pháp giải:
+) P = A : B
+) Muốn chia đa thức A cho đa thức B, ta làm như sau:
Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B.
Bước 2: Lấy A trừ đi tích của B với thương mới thu được ở bước 1
Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B
Bước 4: Lấy dư thứ nhất trừ đi tích B với thương vừa thu được ở bước 3
Bước 5: Làm tương tự như trên
Đến khi dư cuối cùng có bậc nhỏ hơn bậc của B thì quá trình chia kết thúc.
Lời giải:
Ta có: A = B . P nên P = A : B

3. Chia đa thức cho đa thức, trường hợp chia có dư
Phương pháp giải:
Mô tả lại các bước tương tự như chia đa thức cho đa thức trường hợp chia hết.
Lời giải:
Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của D chia cho hạng tử bậc cao nhất của E.
Bước 2: Lấy D trừ đi tích của E với thương mới thu được ở bước 1
Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của E
Bước 4: Lấy dư thứ nhất trừ đi tích E với thương vừa thu được ở bước 3. Ta được dư thứ hai có bậc nhỏ hơn bậc của E thì quá trình chia kết thúc.
Phương pháp giải:
Đa thức bậc n không chia được cho đa thức bậc m (n < m)
Lời giải:
Lúc này phép chia không thực hiện được nữa vì bậc của đa thức -6x + 10 (là 1) nhỏ hơn bậc của đa thức chia x2 + 1 (là 2)
Hoạt động 5 trang 42 Toán lớp 7 SGK Tập 2: Hãy kiểm tra lại đẳng thức D = E . (5x – 3) + G
Phương pháp giải:
Bước 1: Thực hiện phép nhân đa thức E .(5x – 3)
Bước 2: Thực hiện phép cộng đa thức tìm được ở bước 1 với đa thức G
Nếu kết quả = đa thức D thì đúng
Lời giải:
Ta có: E . (5x – 3) + G
= (x2 + 1) . (5x – 3) + (-6x + 10)
= x2 .(5x – 3) + 1. (5x – 3) + (-6x) + 10
= x2 . 5x + x2 . (-3) + 5x – 3 – 6x + 10
= 5x3 – 3x2 + (5x – 6x) + (-3 + 10)
= 5x3 – 3x2 – x + 7
= D
Vậy đẳng thức đúng.
Phương pháp giải:
+) Muốn chia đa thức A cho đa thức B, ta làm như sau:
Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B.
Bước 2: Lấy A trừ đi tích của B với thương mới thu được ở bước 1
Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B
Bước 4: Lấy dư thứ nhất trừ đi tích B với thương vừa thu được ở bước 3
Bước 5: Làm tương tự như trên
Đến khi dư cuối cùng có bậc nhỏ hơn bậc của B thì quá trình chia kết thúc.
+) Viết A = B. Q + R
Lời giải:
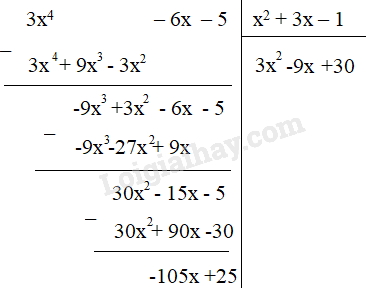
Vậy A = (x2+ 3x – 1) . (3x2 – 9x + 30) - 105x + 25
Thử thách nhỏ trang 42 Toán lớp 7 SGK Tập 2: Em có biết tại sao Vuông làm nhanh thế không?

Phương pháp giải:
Xét phép chia (A + B) : C với bậc của B nhỏ hơn bậc của C
Nếu A chia C không dư thì số dư của (A + B ) : C là B
Lời giải:
Ta có: x3 – 3x2 + x – 1 = (x3 – 3x2 ) + (x -1).
Vì x3 – 3x2 chia cho x2 – 3x không dư ; bậc của x – 1 nhỏ hơn bậc của x2 – 3x nên số dư của phép chia (x3 – 3x2 ) + (x -1) cho x2 – 3x là x – 1
Vậy Vuông làm nhanh và đúng.
Bài tập
Bài 7.30 trang 43 Toán lớp 7 SGK Tập 2: Tính:
a) 8x5 : 4x3
b) 120x7 : (-24x5)
c) 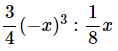
d) -3,72x4 : (-4x2)
Phương pháp giải:
Bước 1: Chia 2 hệ số
Bước 2: Chia 2 lũy thừa của biến
Bước 3: Nhân 2 kết quả trên, ta được thương
Lời giải:
a) 8x5 : 4x3 = (8 : 4) . (x5 : x3) = 2.x2
b) 120x7 : (-24x5) = [120 : (-24)] . (x7 : x5) = -5.x2
c) 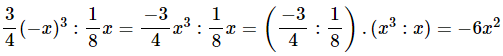
d) -3,72x4 : (-4x2) = [(-3,72) : (-4)] . (x4 : x2) = 0,93x2
Bài 7.31 trang 43 Toán lớp 7 SGK Tập 2: Thực hiện các phép chia đa thức sau:
a) (-5x3 + 15x2 + 18x) : (-5x)
b) (-2x5 – 4x3 + 3x2) : 2x2
Phương pháp giải:
Muốn chia đa thức cho đơn thức, ta chia từng hạng tử của đa thức cho đơn thức rồi tổng các kết quả thu được.
Lời giải:
a) (-5x3 + 15x2 + 18x) : (-5x)
= (-5x3) : (-5x) + 15x2 : (-5x) + 18x : (-5x)
= [(-5): (-5)] . (x3 : x) + [15 : (-5)] . (x2 : x) + [18 : (-5)]. (x : x)
= x2 – 3x - ![]()
b) (-2x5 – 4x3 + 3x2) : 2x2
= (-2x5 : 2x2) + (-4x3 : 2x2) + (3x2 : 2x2)
= [(-2) : 2] . (x5 : x2) + [(-4) : 2] . (x3 : x2) + (3 : 2) . (x2 : x2)
= -x3 – 2x + ![]()
Bài 7.32 trang 43 Toán lớp 7 SGK Tập 2: Thực hiện phép chia đa thức sau bằng cách đặt tính chia:
a) (6x3 – 2x2 – 9x + 3) : (3x – 1)
b) (4x4 + 14x3 – 21x – 9) : (2x2 – 3)
Phương pháp giải:
+) Muốn chia đa thức A cho đa thức B, ta làm như sau:
Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B.
Bước 2: Lấy A trừ đi tích của B với thương mới thu được ở bước 1
Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B
Bước 4: Lấy dư thứ nhất trừ đi tích B với thương vừa thu được ở bước 3
Bước 5: Làm tương tự như trên
Đến khi dư cuối cùng có bậc nhỏ hơn bậc của B thì quá trình chia kết thúc.
Lời giải:
a, 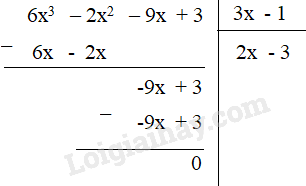
b, 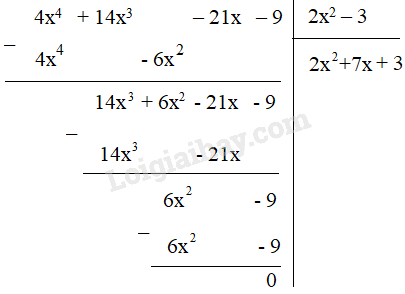
a) n = 2
b) n = 3
Phương pháp giải:
Muốn chia đa thức cho đơn thức, ta chia từng hạng tử của đa thức cho đơn thức rồi tổng các kết quả thu được.
Lời giải:
a) (0,5x5 + 3,2x3 – 2x2 ) : 0,25x2
= 0,5x5 : 0,25x2 + 3,2x3 : 0,25x2 + (2x2 : 0,25x2)
= (0,5:0,25).(x5 : x2) + (3,2 : 0,25). (x3 : x2 ) + (2 : 0,25). (x2 : x2)
= 2x3 + 12,8x + 4
b) (0,5x5 + 3,2x3 – 2x2 ) : 0,25x3

F(x) = G(x) . Q(x) + R(x)
a) F(x) = 6x4 – 3x3 + 15x2 + 2x – 1 ; G(x) = 3x2
b) F(x) = 12x4 + 10x3 – x – 3 ; G(x) = 3x2 + x + 1
Phương pháp giải:
+) Muốn chia đa thức A cho đa thức B, ta làm như sau:
Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B.
Bước 2: Lấy A trừ đi tích của B với thương mới thu được ở bước 1
Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B
Bước 4: Lấy dư thứ nhất trừ đi tích B với thương vừa thu được ở bước 3
Bước 5: Làm tương tự như trên
Đến khi dư cuối cùng có bậc nhỏ hơn bậc của B thì quá trình chia kết thúc.
+) Viết A = B. Q + R
Lời giải:
a, 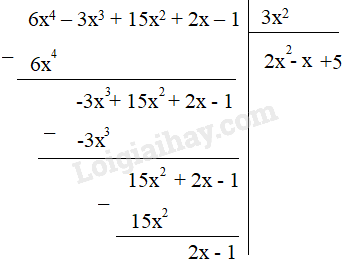
Thương Q(x) = 2x2 – x + 5
Dư R(x) = 2x – 1
Ta có: F(x) = 3x2 . (2x2 – x + 5) + 2x – 1
b, 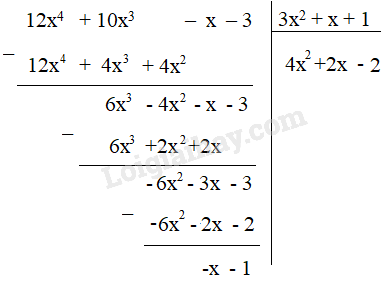
Thương Q(x) = 4x2 + 2x – 2
Dư R(x) = -x – 1
Ta có: F(x) = (3x2 + x + 1) . (4x2 + 2x – 2) – x – 1
Phương pháp giải:
Khi đa thức bị chia có bậc nhỏ hơn bậc của đa thức chia thì thương là 0, số dư là đa thức chia
Lời giải:
Chia đa thức 21x – 4 cho 3x2 được thương là 0, dư 21x – 4
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.