Toptailieu.vn giới thiệu Giải bài tập Toán lớp 7 trang 66, 67, 68, 69 Bài 33: Quan hệ giữa ba cạnh của một tam giác sách Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7 Tập 2. Mời các bạn đón xem:

Giải Toán lớp 7 trang 66, 67, 68, 69 Bài 33: Quan hệ giữa ba cạnh của một tam giác

1. Bất đẳng thức tam giác

Hoạt động 1 trang 66 Toán lớp 7 SGK Tập 2: Cho hai bộ ba thanh tre nhỏ có độ dài như sau:

Bộ thứ nhất: 10 cm, 20 cm, 25 cm.

Bộ thứ hai: 5 cm, 15 cm, 25 cm.

Em hãy ghép và cho biết bộ nào ghép được thành một tam giác.

Phương pháp giải:

Ghép sao cho cứ 2 đầu của 2 thanh tre trùng nhau thì bộ ba đó ghép được thành tam giác.

Lời giải:

Bộ thứ nhất ghép được thành tam giác.

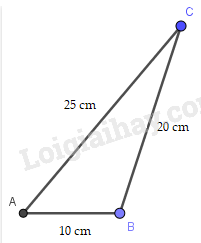
Hoạt động 2 trang 66 Toán lớp 7 SGK Tập 2: Với bộ ba thanh tre ghép lại được thành một tam giác trong HĐ1, em hãy so sánh độ dài của thanh tre bất kì với tổng độ dài 2 thanh còn lại

Phương pháp giải:

Tính tổng độ dài của 2 thanh tre bất kì rồi so sánh với dộ dài thanh còn lại.

Lời giải:

Ta có: 10 + 20 = 30 > 25

10 + 25 = 35 > 20

20 + 25 = 45 > 10

Vậy độ dài của thanh tre bất kì luôn nhỏ hơn tổng độ dài 2 thanh còn lại.

Tranh luận trang 67 Toán lớp 7 SGK Tập 2: Ý kiến của em thì sao?

Phương pháp giải:

Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại.

Kiểm tra, nếu ba độ dài không thỏa mãn bất đẳng thức tam giác thì chúng không ghép được thành một tam giác.

Lời giải:

Vì 1+ 2 < 4 nên bộ ba đoạn thẳng không lập được thành 1 tam giác.

Vậy Vuông sai, Tròn đúng.

Chú ý: Khi kiểm tra 3 đoạn thẳng có thỏa mãn bất đẳng thức tam giác không, để nhanh gọn, ta chỉ cần kiểm tra tổng độ dài của 2 cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất hay không

Luyện tập trang 68 Toán lớp 7 SGK Tập 2: Hỏi ba độ dài nào sau đây không thể là độ dài ba cạnh của một tam giác? Vì sao? Hãy vẽ tam giác nhận ba độ dài còn lại làm độ dài 3 cạnh.

a) 5 cm, 4 cm, 6 cm.

b) 3 cm, 6 cm, 10 cm.

Phương pháp giải:

Khi kiểm tra 3 đoạn thẳng có thỏa mãn bất đẳng thức tam giác không, để nhanh gọn, ta chỉ cần kiểm tra tổng độ dài của 2 cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất hay không

Lời giải:

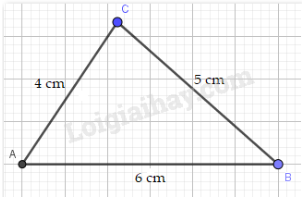
a) Vì 5+4 > 6 nên ba độ dài 5 cm, 4 cm, 6 cm có thể là độ dài ba cạnh của một tam giác.

b) Vì 3 + 6 = 9 < 10 nên ba độ dài 3 cm, 6 cm, 10 cm không thể là độ dài ba cạnh của một tam giác

Vận dụng trang 68 Toán lớp 7 SGK Tập 2: Trở lại tình huống mở đầu, em hãy giải thích vì sao nếu dựng cột điện ở vị trí C trên đoạn thẳng AB thì tổng độ dài dây dẫn điện cần sử dụng là ngắn nhất? (H.9.17)

Phương pháp giải:

Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại.

Lời giải:

+) Nếu A,B,C không thẳng hàng thì ta lập được tam giác ABC. Khi đó, theo bất đẳng thức tam giác, ta có:

AC + CB > AB, tức là độ dài dây dẫn luôn lớn hơn AB.

+) Nếu A,B,C thẳng hàng thì C nằm giữa A và B nên AC + CB = AB, tức là độ dài dây dẫn bằng AB.

Vậy khi C nằm trên đoạn thẳng AB thì tổng độ dài dây dẫn điện cần sử dụng là ngắn nhất.

Bài tập

Bài 9.10 trang 69 Toán lớp 7 SGK Tập 2: Cho các bộ ba đoạn thẳng có độ dài như sau:

a) 2 cm, 3 cm, 5 cm

b) 3 cm, 4 cm, 6 cm

c) 2 cm, 4 cm, 5 cm.

Hỏi bộ ba nào không thể là độ dài ba cạnh của một tam giác? Vì sao? Với mỗi bộ ba còn lại, hãy vẽ một tam giác có độ dài ba cạnh được cho trong bộ ba đó

Phương pháp giải:

Khi kiểm tra 3 đoạn thẳng có thỏa mãn bất đẳng thức tam giác không, để nhanh gọn, ta chỉ cần kiểm tra tổng độ dài của 2 cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất hay không

Lời giải:

Theo bất đẳng thức tam giác:

a) Vì 2 + 3 = 5 nên bộ ba đoạn thẳng có độ dài 2 cm, 3 cm, 5 cm không thể là độ dài ba cạnh của một tam giác

b) Vì 3+4 > 6 nên bộ ba đoạn thẳng có độ dài 3 cm, 4 cm, 6 cm có thể là độ dài ba cạnh của một tam giác

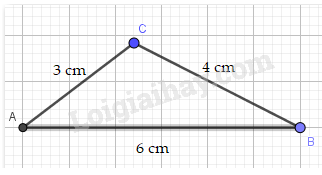
* Cách vẽ: + Vẽ độ dài cạnh AB = 6cm.

+ Dùng compa, vẽ cung tròn tâm A bán kính 3 cm, cung tròn tâm B bán kính 4cm. Hai cung tròn này cắt nhau tại C.

Ta được tam giác ABC cần vẽ.

c) Vì 2+4 > 5 nên bộ ba đoạn thẳng có độ dài 2 cm, 4 cm, 5 cm có thể là độ dài ba cạnh của một tam giác

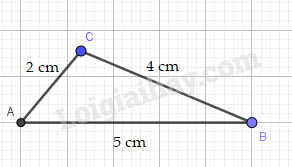
* Cách vẽ: + Vẽ độ dài cạnh AB = 5cm.

+ Dùng compa, vẽ cung tròn tâm A bán kính 2 cm, cung tròn tâm B bán kính 4cm. Hai cung tròn này cắt nhau tại C.

Ta được tam giác ABC cần vẽ.

Bài 9.11 trang 69 Toán lớp 7 SGK Tập 2: a) Cho tam giác ABC có AB = 1 cm, BC = 7 cm. Hãy tìm độ dài cạnh CA biết rằng đó là một số nguyên ( cm).

b) Cho tam giác ABC có AB= 2 cm, BC = 6 cm và BC là cạnh lớn nhất. Hãy tìm độ dài cạnh CA biết rằng đó là một số nguyên ( cm).

Phương pháp giải:

Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại và lớn hơn hiệu độ dài 2 cạnh còn lại: b – c < a < b + c ( với a, b, c là độ dài 3 cạnh của tam giác)

Kết hợp điều kiện độ dài cạnh CA là số nguyên

Lời giải:

Áp dụng bất đẳng thức tam giác trong tam giác ABC, ta có:

7 – 1 < CA < 7 + 1

6 < CA < 8

Mà CA là số nguyên

CA = 7 cm.

Vậy CA = 7 cm.

b) Áp dụng bất đẳng thức tam giác trong tam giác ABC, ta có:

AB + CA > BC

2 + CA > 6

CA > 4 cm

Mà CA là số nguyên và CA < 6 ( vì BC = 6 cm là cạnh lớn nhất của tam giác)

CA = 5 cm

Vậy CA = 5 cm.

Bài 9.12 trang 69 Toán lớp 7 SGK Tập 2: Cho điểm M nằm bên trong tam giác ABC. Gọi N là giao điểm của đường thẳng AM và cạnh BC. (H.9.18)

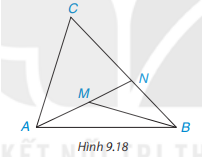
a) So sánh MB với MN + NB, từ đó suy ra MA + MB < NA + NB

b) So sánh NA với CA + CN, từ đó suy ra NA + NB < CA + CB

c) Chứng minh MA + MB < CA + CB.

Phương pháp giải:

Sử dụng định lí:

+ Trong các đường xiên và đường vuông góc kẻ từ 1 điểm nằm ngoài 1 đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất.

+ Trong một tam giác, cạnh đối diện với góc lớn nhất là cạnh lớn nhất.

Lời giải:

a) 3 điểm M,N,B không thẳng hàng.

Áp dụng bất đẳng thức tam giác trong tam giác MNB có:

MB < MN + NB

MA + MB < MA + MN + NB

MA + MB < NA + NB ( vì MA + MN = NA) (1)

b) 3 điểm A,N,C không thẳng hàng.

Áp dụng bất đẳng thức tam giác trong tam giác ACN có:

NA < CA + CN

NA + NB < CA + CN + NB

NA + NB < CA + CB ( vì CN + NB = CB) (2)

c) Từ (1) và (2) ta có:

MA + MB < NA + NB < CA + CB

Vậy MA + MB < CA + CB

Bài 9.13 trang 69 Toán lớp 7 SGK Tập 2: Cho tam giác ABC, điểm D nằm giữa B và C. Chứng minh rằng AD nhỏ hơn nửa chu vi tam giác ABC.

Phương pháp giải:

Áp dụng quan hệ giữa ba cạnh của tam giác ABD và tam giác ACD.

Lời giải:

Áp dụng quan hệ giữa ba cạnh của tam giác ABD, ta có: AD < AB + BD

Áp dụng quan hệ giữa ba cạnh của tam giác ACD, ta có: AD < CD + AC

=> AD + AD < AB + BD + CD + AC

=> 2AD < AB + BC + AC (vì DB + DC = BC)

=> 2AD < Chu vi tam giác ABC hay AD < (Chu vi tam giác ABC) : 2

Vậy AD nhỏ hơn nửa chu vi tam giác ABC.