SBT Toán 7 Kết nối tri thức: Ôn tập chương IX

Giang Ngày: 01-02-2023 Lớp 7

700

Toptailieu biên soạn và giới thiệu giải sách bài tập Toán 7 Ôn tập chương IX sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 7 Ôn tập chương IX.

Giải SBT Toán 7 (Kết nối tri thức): Ôn tập chương IX

Câu hỏi 1 trang 59 sách bài tập Toán 7: Tìm phương án Sai trong câu sau: Trong tam giác

A.đối diện với góc lớn nhất là cạnh lớn nhất

B.đối diện với cạnh bé nhất là góc nhọn

C.đối diện với cạnh lớn nhất là góc tù

D.đối diện với góc tù (nếu có) là cạnh lớn nhất.

Phương pháp giải

Quan hệ giữa góc và cạnh đối diện trong một tam giác

Lời giải

Chọn C

Câu hỏi 2 trang 59 sách bài tập Toán 7: Bộ ba số nào sau đây không là độ dài ba cạnh của một tam giác?

A.7, 5, 7

B.7, 7, 7

C.3, 5, 4

D.4, 7, 3

Phương pháp giải

Áp dụng bất đẳng thức tam giác

Nếu cạnh lớn nhất nhỏ hơn tổng 2 cạnh còn lại thì bộ ba số có là độ dài ba cạnh của một tam giác.

Lời giải

4 + 3 = 7 => Bộ ba số 4,7,3 không là độ dài ba cạnh của một tam giác.

Chọn D

Câu hỏi 3 trang 59 sách bài tập Toán 7: Tam giác cân có độ dài cạnh bên b, độ dài cạnh đáy d thì ta phải có:

A.d > b

B.d = 2b

C.d < b/2

D. d < 2b

Phương pháp giải

Áp dụng bất đẳng thức tam giác

Trong tam giác cân, 2 cạnh bên bằng nhau

Lời giải

Tam giác có 2 cạnh bên là b, áp dụng bất đẳng thức trong tam giác:

b + b > d => 2b > d.

Chọn D

Câu hỏi 4 trang 59 sách bài tập Toán 7: Với mọi tam giác ta đều có:

A.mỗi cạnh lớn hơn nửa chu vi

B.mỗi cạnh lớn hơn hoặc bằng nửa chu vi

C.mỗi cạnh nhỏ hơn nửa chu vi

D.cả ba trường hợp trên đều có thể xảy ra.

Phương pháp giải

Áp dụng bất đẳng thức tam giác

Lời giải

Ba cạnh bất kì trong tam giác:a, b, c

Theo bất đẳng thức tam giác: a < b + c =>a + a < a + b + c

Vậy mỗi cạnh nhỏ hơn nửa chu vi.

Câu hỏi 5 trang 59 sách bài tập Toán 7: Xét hai đường trung tuyến BM, CN của tam giác ABC có BC = 4cm. Trong các số sau, số nào có thể là tổng độ dài BM + CN?

A.5 cm

B.5,5 cm

C.6 cm

D.6,5 cm

Phương pháp giải

Áp dụng bất đẳng thức tam giác

Tính chất trọng tâm tam giác

Lời giải

G là trọng tâm tam giác ABC

Xét tam giác GBC có GB + GC > BC ( Bất đẳng thức tam giác)

$\begin{array}{l} \Rightarrow \frac{2}{3} (B M + C N) > B C \\ \Rightarrow B M + C N > \frac{3}{2} B C = 6 \end{array}$

Chọn D.

Câu hỏi 6 trang 59 sách bài tập Toán 7: Tam giác ABC có số đo ba góc thoả mãn: $\hat{A} = \hat{B} + \hat{C}$ . Hai tia phân giác của góc A và góc B cắt nhau tại điểm I. Khi đó góc BIC có số đo là:

A. $120^{0}$

B. $125^{0}$

C. $130^{0}$

D. $135^{0}$

Phương pháp giải

Áp dụng định lí về tổng ba góc trong tam giác; tính chaasrt tia phân giác của một góc.

Lời giải

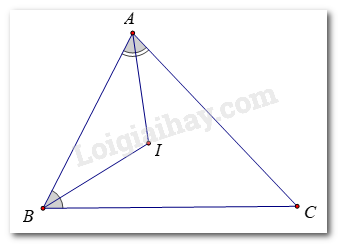
Tam giác ABC có số đo ba góc thoả mãn: góc A = B+ C. Hai tia phân giác (ảnh 1)

Ta có:

$\hat{A} + \hat{B} + \hat{C} = 180^{0}$ (Tổng ba góc trong tam giác)

Mà $\hat{A} = \hat{B} + \hat{C}$

$\begin{array}{l} \Rightarrow (\hat{B} + \hat{C}) + \hat{B} + \hat{C} = 180^{0} \\ \Rightarrow 2 (\hat{B} + \hat{C}) = 180^{0} \\ \Rightarrow \hat{B} + \hat{C} = 180^{0} : 2 = 90^{0} \\ \Rightarrow \hat{A} = \hat{B} + \hat{C} = 90^{0} \end{array}$

Xét tam giác BIC có:

$\hat{B I C} = 180^{0} - (\hat{\frac{B}{2}} + \frac{\hat{C}}{2}) = 180^{0} - \frac{90^{0}}{2} = 180^{0} - 45^{0} = 135^{0}$ .

Chọn D.

Bài 9.23 trang 60 sách bài tập Toán 7: Cho D là một điểm bên trong tam giác ABC. Chứng minh:

a) $\hat{B D C} > \hat{B A C}$

b) BD + DC < AB + AC

Phương pháp giải

- Tia AD chia góc A thành góc A1 và góc A2, chia góc BDC thành góc D1 và góc D2.

-Áp dụng tính chất góc ngoài của tam giác

- Gọi E là giao điểm của BD và AC. Ta có:

AB + AC = AB + (AE + EC) = (AB + AE) + EC

-Áp dụng các bất đẳng thức cho tam giác: ABE, DEC

Lời giải

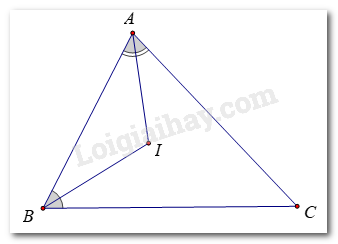
Tìm giá trị của x biết rằng: a) 3x^2 – 3x(x – 2) = 36 (ảnh 1)

Tia AD chia góc A thành góc A1 và góc A2, chia góc BDC thành góc D1 và góc D2.

Góc D1 là góc ngoài tại đỉnh D của tam giác ABD nên:

$\hat{D_{1}} > \hat{A_{1}}$

Góc D2 là góc ngoài tại đỉnh D của tam giác ADC nên:

$\hat{D_{2}} > \hat{A_{2}}$

$\Rightarrow \hat{D} = \hat{D_{1}} + \hat{D_{2}} > \hat{A_{1}} + \hat{A_{2}} = \hat{A}$

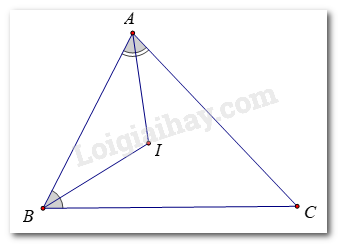
Tìm giá trị của x biết rằng: a) 3x^2 – 3x(x – 2) = 36 (ảnh 2)

Gọi E là giao điểm của BD và AC. Ta có:

AB + AC = AB + (AE + EC) = (AB + AE) + EC

Mà: AB + AE > BE (bất đẳng thức trong tam giác ABE)

=>(AB + AE) + EC > BE + EC = (BD + DE) + EC = BD + (DE + EC)

Mà DE + EC > DC (bất đẳng thức trong tam giác DEC)

=>AB + AC > BD + DC.

Bài 9.24 trang 60 sách bài tập Toán 7: Cho M là một điểm tuỳ ý bên trong tam giác đều ABC. Lấy điểm N nằm khác phía với M đối với đường thẳng AC sao cho $\hat{C A N} = \hat{B A M}$ và AN = AM.

Chứng minh:

a) Tam giác AMN là tam giác đều

b) $Δ M A B = Δ N A C$

c) MN = MA, NC = MB

Phương pháp giải

a)Tam giác AMN cân có 1 góc bằng 60 độ

b) Cm: $Δ M A B = Δ N A C$ (c – g – c )

c) Áp dụng ý a, b.

Lời giải

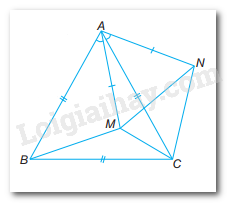
Thực hiện các phép tính sau: a) (x^3 – 8) : (x – 2); b) (x – 1)(x + 1)(x^2 + 1) (ảnh 1)

Tam giác ABC là tam giác đều nên: $\hat{A} = \hat{B} = \hat{C} = 60^{0}$

Ta có:

$\begin{array}{l} \hat{M A N} = \hat{M A C} + \hat{C A N} = \hat{M A C} + \hat{B A M} (d o \hat{C A N} = \hat{B A M}) \\ \Rightarrow \hat{M A N} = \hat{B A C} = 60^{0} \end{array}$

Xét tam giác AMN có: AM = AN (gt)

$\Rightarrow Δ A M N$ cân tại A

Mà $\hat{M A N} = 60^{0} \Rightarrow Δ A B C$ là tam giác đều.

Xét $Δ M A B$ và $Δ N A C$ có:

AB = AC (gt)

AM = AN (gt)

$\hat{M A B} = \hat{N A C}$ (gt)

$\Rightarrow$ $Δ M A B$ = $Δ N A C$ (c – g – c)

Tam giác AMN đều (cm ý a)

$\Rightarrow$ MN = MA

$Δ M A B$ = $Δ N A C$ (cm ý b)

$\Rightarrow M B = N C$ (cạnh tương ứng)

Bài 9.25 trang 60 sách bài tập Toán 7: Xét tam giác ABC vuông tại A; đường phân giác góc B cắt cạnh AC tại E; đường thẳng qua E vuông góc với BC cắt đường thẳng AB tại K. Chứng minh:

a)AE < EC

b) BK = BC.

Phương pháp giải

-Chứng minh: EA = EH (Điểm nằm trên tia phân giác của góc thì cách đều 2 cạnh của góc đó).

-Áp dụng mối liên hệ giữa cạnh huyền và cạnh góc vuông.

Chứng minh tam giác BCK cân tại B.

Lời giải

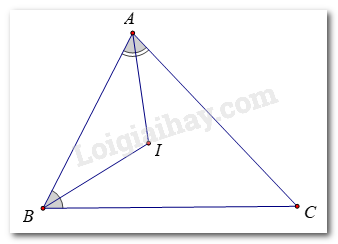
Trong một trò chơi ở câu lạc bộ Toán học, chủ trò viết lên bảng (ảnh 1)

Đường thẳng EK cắt BC tại H

Ta có: E nằm trên đường phân giác góc B

$\Rightarrow E A = E H$ (T/c)

Lại có: Tam giác EHC vuông tại H có: EH là cạnh góc vuông, EC là cạnh huyền

$\Rightarrow E H < E C$ (mlh giữa cạnh huyền và cạnh góc vuông)

$\Rightarrow E A < E C$ .

Xét tam giác BCK có:

${\begin{cases} K H ⊥ B C \\ C A ⊥ B K \end{cases}$

$\Rightarrow$ CH, BK là đường cao trong tam giác BCK

Mà CH cắt BK tại E

$\Rightarrow$ E là trực tâm tam giác BCK

$\Rightarrow$ BE là đường cao

$\Rightarrow$ BE vừa là đường phân giác, vừa là đường cao xuất phát từ B của tam giác BCK

$\Rightarrow$ Tam giác BCK cân tại B.

$\Rightarrow$ BC = BK.

Bài 9.26 trang 60 sách bài tập Toán 7: Cho C là trung điểm của đoạn thẳng AB. Gọi Ax, By là hai đường thẳng vuông góc với AB tại A và tại B. Một đường thẳng qua C cắt Ax tại M, cắt By tại P. Điểm N nằm trên tia đối của tia BP sao cho góc MCN là góc vuông. Gọi H là hình chiếu của C trên MN.

Chứng minh:

a)AM + BN = MN;

b) CM là đường trung trực của AH, CN là đường trung trực của BH;

c) Góc AHB là góc vuông.

Phương pháp giải

-Chứng minh AM = MH: $Δ A M C = Δ H M C$

-Chứng minh:NB = NH: $Δ C H N = Δ C B N (c h - g n)$

b)Áp dụng kết quả ý a

c)Trong tam giác đường trung tuyến ứng với 1 cạnh và bằng nửa cạnh đó thì tam giác đó là tam giác vuông

Lời giải

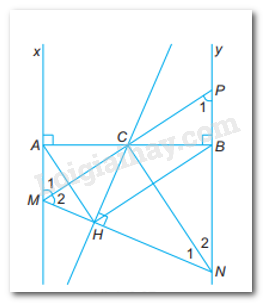
Tìm số b sao cho đa thức x^3 – 3x^2 + 2x – b chia hết cho đa thức x – 3 (ảnh 1)

-Chứng minh AM = MH

Xét $Δ A M C$ và $Δ B P C$ có:

AC = CB (gt)

$\hat{M A C} = \hat{P B C} = 90^{0}$

$\hat{A C M} = \hat{B C P}$ (đối đỉnh)

$\Rightarrow$ $Δ A M C$ = $Δ B P C$ (g – c – g)

$\Rightarrow$ MC = CP (cạnh tương ứng)

Mà $N C ⊥ M P$

$\Rightarrow$ NC là đường trung trực của MP

$\Rightarrow$ Tam giác NMP cân tại N

$\Rightarrow$ $\hat{P_{1}} = \hat{M_{2}}$

Mà $\hat{P_{1}} = \hat{M_{1}}$ (so le trong: Mx // By)

$\Rightarrow \hat{M_{1}} = \hat{M_{2}}$

Xét $Δ A M C$ và $Δ H M C$ có:

$\begin{array}{l} \hat{M A C} = \hat{M H C} = 90^{0} \\ M C : c h u n g \\ \hat{M_{1}} = \hat{M_{2}} (c m t) \\ \Rightarrow Δ A M C = Δ H M C (c h - g n) \\ \Rightarrow A M = M H (c t u) \end{array}$

-Chứng minh:NB = NH

Tam giác MNP cân tại N có NC là đường trung trực đồng thời là đường phân giác xuất phát từ N.

Xét $Δ H N C$ và $Δ B N C$ có:

CN: chung

$\begin{array}{l} \hat{N_{1}} = \hat{N_{2}} (c m t) \\ \hat{C H N} = \hat{C B N} = 90^{0} \\ \Rightarrow Δ C H N = Δ C B N (c h - g n) \end{array}$
$\Rightarrow N H = N B$ (cạnh tương ứng)