Với Giải SBT Toán 7 Bài 9.26 trang 60 Tập 2 trong Ôn tập chương IX Sách bài tập Toán lớp 7 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7.
Cho C là trung điểm của đoạn thẳng AB. Gọi Ax, By là hai đường thẳng
Bài 9.26 trang 60 sách bài tập Toán 7: Cho C là trung điểm của đoạn thẳng AB. Gọi Ax, By là hai đường thẳng vuông góc với AB tại A và tại B. Một đường thẳng qua C cắt Ax tại M, cắt By tại P. Điểm N nằm trên tia đối của tia BP sao cho góc MCN là góc vuông. Gọi H là hình chiếu của C trên MN.
Chứng minh:
a)AM + BN = MN;
b) CM là đường trung trực của AH, CN là đường trung trực của BH;
c) Góc AHB là góc vuông.
Phương pháp giải
a)
-Chứng minh AM = MH: ΔAMC=ΔHMC
-Chứng minh:NB = NH:ΔCHN=ΔCBN(ch−gn)
b)Áp dụng kết quả ý a
c)Trong tam giác đường trung tuyến ứng với 1 cạnh và bằng nửa cạnh đó thì tam giác đó là tam giác vuông
Lời giải
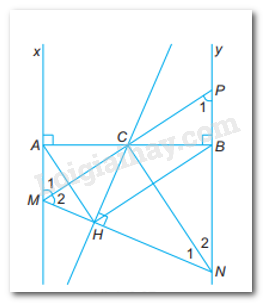
a)
-Chứng minh AM = MH
Xét ΔAMC và ΔBPC có:
AC = CB (gt)
^MAC=^PBC=900
^ACM=^BCP(đối đỉnh)
⇒ΔAMC = ΔBPC(g – c – g)
⇒ MC = CP (cạnh tương ứng)
Mà NC⊥MP
⇒NC là đường trung trực của MP
⇒Tam giác NMP cân tại N
⇒^P1=^M2
Mà ^P1=^M1(so le trong: Mx // By)
⇒^M1=^M2
Xét ΔAMC và ΔHMC có:
^MAC=^MHC=900MC:chung^M1=^M2(cmt)⇒ΔAMC=ΔHMC(ch−gn)⇒AM=MH(ctu)
-Chứng minh:NB = NH
Tam giác MNP cân tại N có NC là đường trung trực đồng thời là đường phân giác xuất phát từ N.
Xét ΔHNC và ΔBNC có:
CN: chung
^N1=^N2(cmt)^CHN=^CBN=900⇒ΔCHN=ΔCBN(ch−gn)
⇒NH=NB(cạnh tương ứng)
⇒AM+BN=MH+HN=MN
b)
Tam giác MAH cân tại M với MC là đường phân giác xuất phát từ đỉnh cân M
⇒MC là đồng thời là đường trung trực của AH
Tam giác NBH cân tại N với NC là đường phân giác xuất phát từ đỉnh cân N
⇒NC đồng thời là đường trung trực của BH.
c)
Xét tam giác HAB có CA = CB
⇒HC là đường trung tuyến
ΔAMC=ΔHMC(cmt) ⇒AC=HC(cạnh tương ứng)
⇒HC=CA=CB
Đường trung tuyến ứng với cạnh AB và bằng nửa cạnh AB.
Vậy tam giác HAB vuông tại H.
Xem thêm lời giải sách bài tập Toán 7 lớp 7 Kết nối tri thức với cuộc sống hay, chi tiết khác:
Câu hỏi 1 trang 59 sách bài tập Toán 7: Tìm phương án Sai trong câu sau: Trong tam giác...
Câu hỏi 4 trang 59 sách bài tập Toán 7: Với mọi tam giác ta đều có...
Bài 9.23 trang 60 sách bài tập Toán 7: Cho D là một điểm bên trong tam giác ABC. Chứng minh...
Xem thêm các bài giải SBT Toán lớp 7 Kết nối với tri thức hay, chi tiết khác:
Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
Bài 36: Hình hộp chữ nhật và hình lập phương
Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.