Toptailieu.vn giới thiệu Giải bài tập Toán lớp 7 trang 84 Bài tập cuối chương IX sách Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7 Tập 2. Mời các bạn đón xem:
Nội dung bài viết
Giải Toán lớp 7 trang 84 Bài tập cuối chương 9
Bài tập
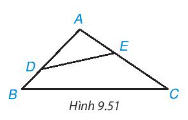
Bài 9.36 trang 84 Toán lớp 7 SGK Tập 2: Cho tam giác ABC có ^BACˆBAC là góc tù. Lấy điểm D nằm giữa A và B, lấy điểm E nằm giữa A và C (H.9.51). Chứng minh DE < BC.
Phương pháp giải:
-Sử dụng tính chất bắc cầu
-Chứng minh DE < DC
-Chứng minh DC < BC
Lời giải:
Ta có ^BACˆBAC là góc tù nên ^ADE,^AEDˆADE,ˆAED là các góc nhọn
⇒^DEC⇒ˆDEC là góc tù
⇒DE<DC⇒DE<DC (quan hệ giữa góc và cạnh đối diện trong tam giác DEC). (1)
Xét tam giác ADC có:
^DACˆDAC là góc tù nên ^ADC,^ACDˆADC,ˆACD là các góc nhọn
⇒^BDC⇒ˆBDC là góc tù.
⇒DC<BC⇒DC<BC (quan hệ giữa góc và cạnh đối diện trong tam giác BDC) (2)
Từ (1) và (2) suy ra: BC > DE
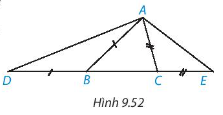
Bài 9.37 trang 84 Toán lớp 7 SGK Tập 2: Cho tam giác ABC ( AB > AC). Trên đường thẳng chứa cạnh BC, lấy điểm D và điểm E sao cho B nằm giữa D và C, C nằm giữa B và E, BD = BA, CE = CA ( H.9.52)
a) So sánh ^ADEˆADE và ^AEDˆAED
b) So sánh các đoạn thẳng AD và AE.
Phương pháp giải:
a) AB>AC⇒^ABC<^ACBAB>AC⇒ˆABC<ˆACB
-Chứng minh .
-^ABD=1800−2^ADBˆABD=1800−2ˆADB,^ACE=1800−2^AECˆACE=1800−2ˆAEC
b)Sử dụng kết quả câu a)
Lời giải:
a) AB>AC⇒^ABC<^ACBAB>AC⇒ˆABC<ˆACB( quan hệ giữa góc và cạnh đối diện trong tam giác ABC)
⇒1800−^ABD<1800−^ACE⇒^ABD>^ACE
Tam giác ABD cân tại B ( BD= BA) ⇒^ABD=1800−2^ADB
Tam giác ACE cân tại C ( CE = CA)⇒^ACE=1800−2^AEC
⇒1800−2^ADB>1800−2^AEC⇒^ADB<^AECHay^ADE<^AED
b) Xét tam giác ADE ta có : ^ADB<^AEC
⇒AD>AE (Mối liên hệ giữa cạnh và góc trong tam giác).
Bài 9.38 trang 84 Toán lớp 7 SGK Tập 2: Gọi AI và AM lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng
a)AI<12(AB+AC)
b)AM<12(AB+AC)
Phương pháp giải:
a)Sử dụng mối liên hệ giữa đường vuông góc và đường xiên, chứng minh AI < AB, AI < AC.
b) Lấy D sao cho M là trung điểm của AD
-Chứng minh AB = CD
-Áp dụng bất đẳng thức tam giác cho tam giác ACD.
Lời giải:
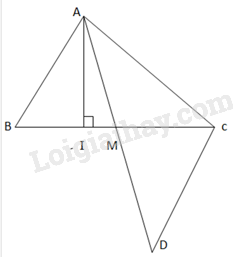
a) AI là đường cao từ A xuống đoạn thẳng BC
⇒AI là khoảng cách từ A đến BC
⇒AI ngắn nhất
⇒{AI<ABAI<AC⇒2AI<AB+AC⇒AI<12(AB+AC)
b) Lấy D sao cho M là trung điểm của AD
Xét ΔABM và DCM có
AM = DM ( M là trung điểm củaAD)
BM = CM ( M là trung điểm của BC)
^AMB=^CMD( 2 góc đối đỉnh)
⇒ΔABM=ΔDCM(c−g−c)
⇒AB=CD(cạnh tương ứng)
Xét ΔADC ta có: AD < AC + CD (bất đẳng thức tam giác)
⇒ 2AM < AC + AB
⇒ AM < 12(AB + AC)
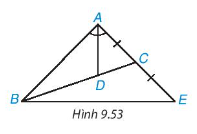
Bài 9.39 trang 84 Toán lớp 7 SGK Tập 2: Cho tam giác ABC có đường phân giác AD, D nằm trên BC sao cho BD= 2DC. Trên đường thẳng AC, lấy điểm E sao cho C là trung điểm của AE (H.9.53). Chứng minh rằng tam giác ABE cân tại A
Gợi ý D là trọng tâm của tam gíac ABE, tam giác này có đường phân giác AD đồng thời là trung tuyến.
Phương pháp giải:
-BD = 2 DC, BC là đường trung tuyến từ đó chứng minh được D là trọng tâm tam giác ABE
-AD là phân giác góc ABE
Lời giải:
C là trung điểm của AE
⇒ BC là trung tuyến của tam giác ABE (1)
D thuộc BC, BD=2DC⇒BD=2(BC−BD)⇒3BD=2BC⇒BD=23BC(2)
Từ (1) và (2) suy ra: D là trọng tâm của tam giác ABE
⇒ AD là đường trung tuyến ứng với BE
mà AD là đường phân giác của ^BAC hay ^ABE thuộc tam giác ABE
⇒ Tam giác ABE cân tại A.
Bài 9.40 trang 84 Toán lớp 7 SGK Tập 2: Một sợi dây thép dài 1,2m. Cần đánh dấu trên sợ dây thép đó hai điểm để khi uốn gập nó lại tại hai điểm đó sẽ tạo thành tam giác cân có một cạnh bằng 30 cm (h.9.54). Em hãy mô tả các cách đánh dấu hai điểm trên sợi dây thép.
Phương pháp giải:
-Chọn cạnh bên bằng 30 cm, tính cạnh đáy?
-Chọn cạnh đáy bằng 30 cm, tính cạnh bên?
Lời giải:
TH1: Cạnh bên bằng 30 cm
Khi đó cạnh đáy bằng: 120 – (30 + 30 ) =60 (cm)
Đánh dấu AB = CD = 30 cm, BC = 60 cm
TH2: Cạnh đáy bằng 30 cm
Khi đó cạnh bên bằng: (120 – 30) : 2 = 45 (cm)
Đánh dấu AB = CD = 45 cm
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.