Toptailieu.vn giới thiệu Giải bài tập Toán lớp 7 trang 82, 83 Luyện tập chung trang 82 sách Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7 Tập 2. Mời các bạn đón xem:

Giải Toán lớp 7 trang 82, 83 Luyện tập chung trang 82

Bài tập

Bài 9.31 trang 83 Toán lớp 7 SGK Tập 2: Chứng minh rằng tam giác có đường trung tuyến và đường cao xuất phát từ cùng một đỉnh trùng nhau là một tam giác cân.

Phương pháp giải:

-Chứng minh ΔABD = ΔACD (c−g−c)

Lời giải:

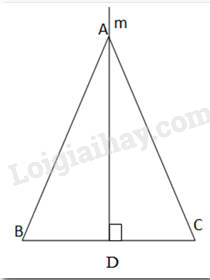
Từ A kẻ đường thẳng m vuông góc với BC tại trung điểm D của BC.

⇒ AD là đường trung tuyến của BC.

Xét ΔABD và ΔACD có:

AD :chung

BD = CD (gt)

⇒ΔABD = ΔACD (c−g−c)

⇒AB = AC (2 cạnh tương ứng)

⇒ ΔABC cân tại A (đpcm).

Bài 9.32 trang 83 Toán lớp 7 SGK Tập 2: Cho ba điểm phân biệt thẳng hàng A, B, C. Gọi d là đường thẳng vuông góc với AB tại A. Với điểm M thuộc d, M khác A, vẽ đường thẳng CM. Qua B kẻ đường thẳng vuông góc với đường thẳng CM, cắt d tại N. Chứng minh đường thẳng BM vuông góc với đường thẳng CN.

Phương pháp giải:

-Ba đường cao trong tam giác đồng quy tại một điểm.

Lời giải:

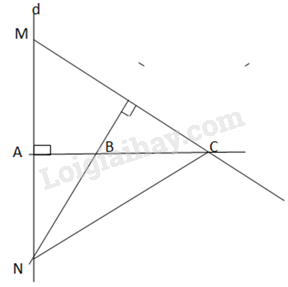
Xét tam giác MNC có

$\begin{array}{l}BN\mathrm{\perp }CM\\ CA\mathrm{\perp }MN\end{array}$

$BN\cap CA=$ {B}

$\Rightarrow$ B là trực tâm của tam giác MNC

$\Rightarrow MB\mathrm{\perp }CN$

Bài 9.33 trang 83 Toán lớp 7 SGK Tập 2: Có một mảnh tôn hình tròn cần đục lỗ ở tâm. Làm thế nào để xác định được tâm của mảnh tôn đó?

Phương pháp giải:

-Lấy ba điểm phân biệt A, B, C trên đường viền ngoài mảnh tôn.

- Xác định giao của các đường trung trực.

Lời giải:

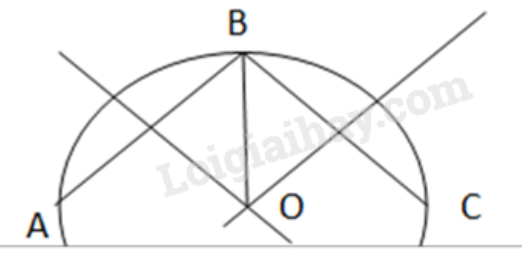
-Lấy ba điểm phân biệt A, B, C trên đường viền ngoài mảnh tôn.

- Vẽ đường trung trực cạnh AB và cạnh BC. Hai đường trung trực này cắt nhau tại O. Khi đó O là tâm cần xác định.

Bài 9.34 trang 83 Toán lớp 7 SGK Tập 2: Cho tam giác ABC. Kẻ tia phân giác At của góc tạo bởi tia AB và tia đối của AC. Chứng minh rằng nếu đường thẳng chứa tia At song song với đường thẳng BC thì tam giác ABC cân tại A.

Phương pháp giải:

$At\parallel BC$

$\widehat{ABC}=\widehat{BAt}$(Hai góc sole trong)

$\widehat{ACB}=\widehat{MAt}$(Hai góc đồng vị)

Lời giải:

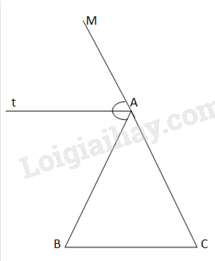
Gọi AM là tia đối của AC. At là đường phân giác của $\widehat{MAB}\Rightarrow \widehat{MAt}=\widehat{BAt}$

Ta có: $At\parallel BC$ nên:

$\widehat{ABC}=\widehat{BAt}$(Hai góc sole trong)

$\widehat{ACB}=\widehat{MAt}$(Hai góc đồng vị)

Mà $\widehat{MAt}=\widehat{BAt}$$\Rightarrow \widehat{ABC}=\widehat{ACB}$

Vậy tam giác ABC cân tại A ( Dấu hiệu nhận biết tam giác cân).

Bài 9.35 trang 83 Toán lớp 7 SGK Tập 2: Kí hiệu $S_{ABC}$ là diện tích tam giác ABC. Gọi G là trọng tâm tam giác ABC, M là trung điểm BC.

a) Chúng minh $S_{GBC}={\displaystyle \frac{1}{3}}{S}_{ABC}$

Gợi ý: Sử dụng $GM={\displaystyle \frac{1}{3}}AM$ để chứng minh $S_{GMB}={\displaystyle \frac{1}{3}}{S}_{ABM},S_{GCM}={\displaystyle \frac{1}{3}}{S}_{ACM}$.

b) Chứng minh $S_{GCA}=S_{GAB}={\displaystyle \frac{1}{3}}{S}_{ABC}$.

Phương pháp giải:

a)

Kẻ  $BP\mathrm{\perp }AM$, $CN\mathrm{\perp }AM$

Sử dụng $GM={\displaystyle \frac{1}{3}}AM$ để chứng minh $S_{GMB}={\displaystyle \frac{1}{3}}{S}_{ABM},S_{GCM}={\displaystyle \frac{1}{3}}{S}_{ACM}$.

b)

-Chứng minh $S_{GAB}=S_{GAC}$

-Sử dụng $S_{ABC}=S_{GAB}+S_{GAC}+S_{GBC}$

Lời giải:

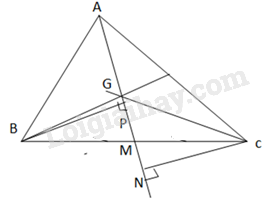
a) Vì G là trọng tâm tam giác ABC nên $GM={\displaystyle \frac{1}{3}}AM$

Kẻ $BP\mathrm{\perp }AM$ ta có

 $\begin{array}{l}{S}_{GMP}={\displaystyle \frac{1}{2}}BP.GM\\ S_{ABM}={\displaystyle \frac{1}{2}}BP.AM\end{array}$

$\Rightarrow {\displaystyle \frac{S_{GMP}}{S_{ABM}}}={\displaystyle \frac{GM}{AM}}={\displaystyle \frac{1}{3}}\Rightarrow S_{GMP}={\displaystyle \frac{1}{3}}{S}_{ABM}$(1)                         

Tương tự, kẻ $CN\mathrm{\perp }AM$, ta có  

$\begin{array}{l}{S}_{GMC}={\displaystyle \frac{1}{2}}CN.GM\\ S_{ACM}={\displaystyle \frac{1}{2}}CN.AM\\ \Rightarrow {\displaystyle \frac{S_{GMC}}{S_{ACM}}}={\displaystyle \frac{GM}{AM}}={\displaystyle \frac{1}{3}}\Rightarrow S_{GMC}={\displaystyle \frac{1}{3}}{S}_{ACM}\left(2\right)\end{array}$

Cộng 2 vế của (1) và (2) ta có: 

$\begin{array}{l}{S}_{GMB}+S_{GMC}={\displaystyle \frac{1}{3}}\left(S_{AMC}+S_{ABM}\right)\\ \Rightarrow S_{GBC}={\displaystyle \frac{1}{3}}{S}_{ABC}\end{array}$

b) 

Ta có

$\begin{array}{l}{S}_{GAB}={\displaystyle \frac{1}{2}}BP.AG\\ S_{GAC}={\displaystyle \frac{1}{2}}CN.AG\end{array}$

Xét $\mathrm{\Delta }BPM$ và $\mathrm{\Delta }CNM$ có:

$\widehat{BPM}=\widehat{CNM}={90}^0$

 BM = CM ( M là trung điểm của BC)

$\widehat{PMB}=\widehat{CMN}$(2 góc đối đỉnh)

$\Rightarrow \mathrm{\Delta }BPM=\mathrm{\Delta }CNM$(cạnh huyền – góc nhọn)

$\Rightarrow$ BP = CN (cạnh tương ứng)

$\Rightarrow S_{GAB}=S_{GAC}$

Ta có: $AG={\displaystyle \frac{2}{3}}AM$

$\begin{array}{l}{S}_{ACB}=S_{GAB}+S_{GAC}+S_{GCB}\\ \Rightarrow S_{ACB}=S_{GAB}+S_{GAC}+{\displaystyle \frac{1}{3}}{S}_{ABC}\\ \Rightarrow {\displaystyle \frac{2}{3}}{S}_{ABC}=2S_{GAC}\\ \Rightarrow {\displaystyle \frac{1}{3}}{S}_{ABC}=S_{GAC}=S_{GAB}\end{array}$