Toptailieu biên soạn và giới thiệu giải sách bài tập Toán 7 Bài tập ôn tập cuối năm sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 7 Bài tập ôn tập cuối năm.
Giải SBT Toán 7 (Kết nối tri thức): Bài tập ôn tập cuối năm
Phương pháp giải
Viết các số dưới dạng phân số với mẫu số chung là 8:
Lời giải
Ta có:
Chia đoạn thẳng đơn vị thành 8 phần bằng nhau, lấy một đoạn làm đơn vị mới. Sau đó, biểu diễn các số hữu tỉ trên trục số.
Bài 2 trang 69 sách bài tập Toán 7: Tính giá trị của biểu thức sau: B = 85 + (-2)12 / 215 + 643
Phương pháp giải
Áp dụng công thức:
Lời giải
Bài 3 trang 69 sách bài tập Toán 7: Bạn Minh đọc một cuốn sách trong ba ngày thì xong. Ngày thứ nhất, Minh đọc được số trang sách. Ngày thứ hai, Minh đọc được số trang sách còn lại. Ngày thứ ba, Minh đọc nốt 36 trang còn lại. Hỏi cuốn sách bạn Minh có bao nhiêu trang?
Phương pháp giải
-Tính số phần trang sách ngày thứ 2 Minh đọc.
-Tính số phần trang sách ngày thứ 3 Minh đọc.
-Ngày thứ 3 đọc được 36 trang, từ đó tính được số trang của cuốn sách.
Lời giải
Ngày thứ 2 Minh đọc số phần trang sách là:
(số trang sách)
Số trang sách còn lại sau 2 ngày là:
(số trang sách)
Theo bài ra, ta có: số trang sách là 36 trang
Cuốn sách của Minh có số trang là:
(trang)
Vậy cuốn sách Minh đọc có 120 trang.
Bài 4 trang 69 sách bài tập Toán 7: a)Không dùng máy tính, hãy tính
b)Trong hai số 1,7(3) và , số nào lớn hơn?
HD:Trước hết hãy dùng máy tính để tính .
Phương pháp giải
-Rút gọn số trong căn
-Bấm máy tính, kiểm tra .
Lời giải
a)
b)
Ta có:
Bài 5 trang 69 sách bài tập Toán 7: a)Trên trục số, hãy xác định điểm biểu diễn số .
b)Viết biểu thức dưới dạng không chứa dấu giá trị tuyệt đối.
Phương pháp giải
nếu
nếu
Lời giải
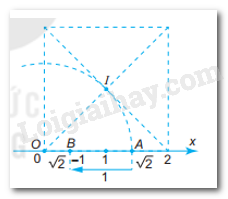
a)
Gọi A là điểm biểu diễn số . Khi đó ta có OA =
Do đó, muốn có điểm B biểu diễn số , từ điểm A, ta di chuyển 1 đơn vị theo chiều âm như hình bên.
Bằng dụng cụ học tập ta xác ssijnh điểm B như sau:
b)Ta có: 1 < 2 nên
Do đó:
Bài 6 trang 69 sách bài tập Toán 7: Trong một đợt phát động làm kế hoạch nhỏ, ba lớp 7A, 7B, 7C tham gia thu gom giấy vụn. Số kilogam giấy vụn gom được của ba lớp này lần lượt tỉ lệ với 2; 4; 5. Biết rằng khối lượng giấy vụn gom được của cả hai lớp 7A và 7C nhiều hơn của lớp 7B là 27 kg. Hỏi mỗi lớp thu gom được bao nhiêu kilogam giấy vụn?
Phương pháp giải
-Gọi x, y, z (kg) lần lượt là khối lượng giấy vụn thu gom được của ba lớp 7A, 7B và 7C.
-
-Áp dụng tính chất dãy tỉ số bằng nhau.
Lời giải
Gọi x, y, z (kg) lần lượt là khối lượng giấy vụn thu gom được của ba lớp 7A, 7B và 7C.
Theo đề bài, ta có:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
Vậy khối lượng giấy vụn của lớp 7A, 7B và 7C thu gom được lần lượt là 18 kg, 36 kg và 45 kg.
Bài 7 trang 69 sách bài tập Toán 7: Xe ô tô và xe máy cùng đi từ tỉnh A đến tỉnh B trên cùng một con đường. Biết rằng xe ô tô đi với vận tốc 80 km/h, xe máy đi với vận tốc 60 km/h. Thời gian đi từ A đến B của xe ô tô ít hơn thời gian đi tương ứng của xe máy là 30 phút. Hãy tính thời gian mỗi xe đi từ A đến B và độ dài quãng đường AB.
Phương pháp giải
-Do 2 xe cùng đi quãng đường AB nên thời gian đi tỉ lệ nghịch với vận tốc đi.
-Áp dụng tính chất dãy tỉ số bằng nhau để tính.
Lời giải
Gọi (giờ) là thời gian xe ô tô khi đi từ A đến B.
Gọi (giờ) là thời gian xe máy khi đi từ A đến B.
Do 2 xe cùng đi quãng đường AB nên thời gian đi tỉ lệ nghịch với vận tốc đi.
Do đó, ta có:
Đổi 30 phút = 0,5 giờ
Theo bài ra, ta có:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
Vậy thời gian để đi từ tỉnh A đến tỉnh B của xe ô tô và xe máy lần lượt là 1,5 giờ và 2 giờ.
Quãng đường AB dài là: S = v.t = 80 . 1,5 = 120 (km)
Bài 8 trang 69 sách bài tập Toán 7: Hai đa thức A(x) và B(x) thoả mãn:
a)Tìm A(x), B(x) rồi xác định bậc, hệ số cao nhất và hệ số tự do của mỗi đa thức đó.
b)Tìm giá trị của mỗi đa thức A(x) và B(x) tại x = -1.
Phương pháp giải
-Lấy vế trái cộng vế trái, vế phải cộng vế phải:
-Thay x = -1 vào 2 đa thức tìm được.
Lời giải
a)
Lấy vế trái cộng vế trái, vế phải cộng vế phải, ta được:
Bậc: 2
Hệ số cao nhất:-1
Hệ số tự do: 1
Mà
Bậc: 3
Hệ số cao nhất: 1
Hệ số tự do: 3
b)
Ta có:
Bài 9 trang 70 sách bài tập Toán 7: Cho đa thức F(x) = x4 - x3 - 6x2 +15x - 9
a)Kiểm tra lại rằng x = 1 và x = -3 là hai nghiệm của F(x).
b)Tìm đa thức G(x) sao cho
Phương pháp giải
Lời giải
a)
Ta có:
Vậy x = 1 và x = -3 là hai nghiệm của F(x).
b)
Ta đặt tính chia:
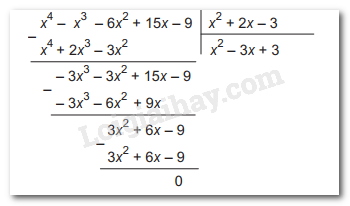
Vậy
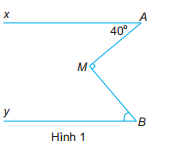
Bài 10 trang 70 sách bài tập Toán 7: Tìm góc MBy trong hình 1, biết rằng Ax // By
HD: Kẻ thêm đường thẳng đi qua M và song song với Ax.
Phương pháp giải
-Kẻ thêm đường thẳng đi qua M và song song với Ax
-Chỉ ra các cặp góc so le trong bằng nhau
-Từ đó, tính được góc MBy.
Lời giải
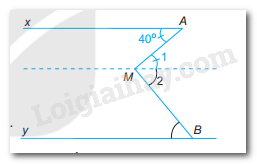
Kẻ thêm đường thẳng đi qua M và song song với Ax.
Từ các đường thẳng song song, ta có:
(2 góc so le trong)
Mà
Mặt khác: (2 góc so le trong).
Bài 11 trang 70 sách bài tập Toán 7: Cho 5 điểm A, B, C, D, E cùng nằm trên một đường thẳng d sao cho AB = DE, BC = CD. Điểm M không thuộc d sao cho MC vuông góc với d. Chứng minh rằng:
a)
b)
Phương pháp giải
-Chứng minh:
-Áp dụng kết quả ý a, chứng minh b)
Lời giải
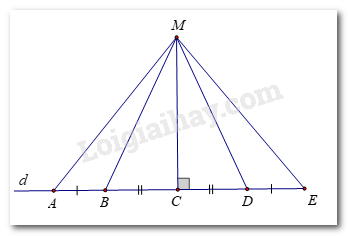
a)
-Xét và có:
-Xét và có:
b)
Xét và có:
MA = ME (cmt)
MB = MD (cmt)
AB = ED (gt)
Bài 12 trang 70 sách bài tập Toán 7: Cho tam giác ABC vuông tại đỉnh A; ba điểm M, N, P lần lượt nằm trên các cạnh BC, CA, AB của tam giác ABC sao cho M là trung điểm của BC, MN vuông góc với AC và MP vuông góc với AB. Chứng minh rằng:
a)
b)
Phương pháp giải
a)
b) Chứng minh tứ giác MNAP là hình chữ nhật.
Lời giải
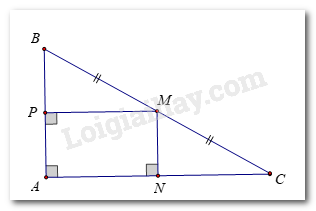
a)
Xét và có:
(cùng phụ với góc B)
b)
Xét tứ giác MNAP có:
Tứ giác MNAP là hình chữ nhật
Bài 13 trang 70 sách bài tập Toán 7: Cho bốn điểm A, B, C và D như Hình 2. Biết rằng góc BEC = 40 độ; góc EBA = 110 độ; AB = CD. Chứng minh rằng:
a)Tam giác BEC cân tại đỉnh E.
b)EA = ED.
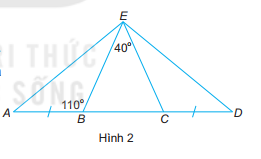
Phương pháp giải
a)Chứng minh
b)Chứng minh: .
Lời giải
a)
Ta có: (2 góc kề bù)
Xét tam giác EBC: (Tổng ba góc trong tam giác)
cân tại E
b)CM: EA = ED
Ta có:
Xét và có:
Bài 14 trang 70 sách bài tập Toán 7: Tròn đưa cho Vuông một tờ giấy, trên đó có vẽ điểm C và hai đường thẳng a và b không đi qua C, cho biết hai đường thẳng a và b không song song với nhau (giao điểm của a và b nằm ngoài tờ giấy). Tròn đố Vuông vẽ được đường thẳng c đi qua C sao cho ba đường thẳng a, b, c đồng quy. Sau một hồi suy nghĩ, Vuông làm như sau (H.3):
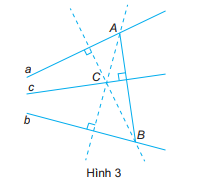
-Vẽ đường thẳng đi qua C và vuông góc với a. Đường thẳng này cắt b tại B.
-Vẽ đường thẳng đi qua C và vuông góc với b. Đường thẳng này cắt a tại A.
Vuông khẳng định rằng đường thẳng c cần vẽ chính là đường thằng đi qua C và vuông góc với AB.
Em hãy giải thích tại sao Vuông lại khẳng định như vậy.
Phương pháp giải
Chứng minh: a, b, c là 3 đường cao trong tam giác.
Lời giải
Xét tam giác ABC, có:
là ba đường cao của tam giác ABC nên chúng đồng quy
b)Cho đoạn thẳng AB. Hãy nêu một cách sử dụng kết quả của câu a để vẽ đường thẳng vuông góc với AB tại A (bằng thước và compa)
Phương pháp giải
- MA = MB = MC
- Chỉ ra các tam giác cân và các góc bằng nhau
- Chứng minh góc A bằng 90 độ.
Lời giải
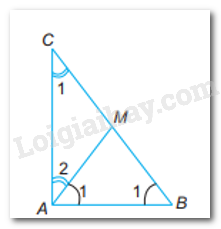
a) Ta có:MA = MB = MC (gt)
là hai tam giác cân tại đỉnh M
Xét tam giác ABC:
(Tổng 3 góc trong 1 tam giác)
b)
Vẽ tam giác cân MAB rồi kéo dài BM về phía M đến điểm C sao cho MC = BM. Khi đó tam giác ABC vuông tại A.
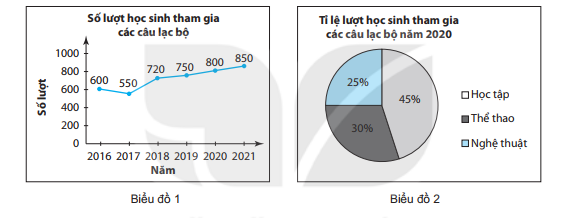
a)Biểu đồ a biểu diễn đại lượng nào theo thời gian?
b)Nêu nhận xét về sự thay đổi số lượt học sinh tham gia các câu lạc bộ từ năm 2016 đến năm 2021.
c)Lập bảng thống kê cho số liệu biểu diễn trong Biểu đồ 2.
d)Tính số lượt học sinh đăng kí trong mỗi câu lạc bộ trong năm 2020.
Phương pháp giải
Dựa vào biểu đồ đọc các dữ liệu
Lời giải
a)Biểu đồ 1 biểu diễn số lượt học sinh tham gia các câu lạc bộ từ năm 2016 đến năm 2021.
b)
Năm 2017, số lượt học sinh tham gia các câu lạc bộ giảm so với năm 2016.
Các năm tiếp theo, số lượt học sinh tham gia các câu lạc bộ đều tăng so với năm trước đó.
c)
Bảng thống kê
|
Câu lạc bộ |
Thể thao |
Nghệ thuật |
Học tập |
|
Tỉ lệ lượt học sinh tham gia (%) |
30 |
25 |
45 |
d)
Tổng số lượt học sinh tham gia các câu lạc bộ năm 2020 là 800 (lượt)
Số lượt học sinh tham gia câu lạc bộ Thể thao là: 800 . 30% = 240 (lượt)
Số lượt học sinh tham gia câu lạc bộ Nghệ thuật là: 800 . 25% = 200 (lượt)
Số lượt học sinh tham gia câu lạc bộ Học tập là: 800 . 45% = 360 (lượt)
Bài 17 tranh 70 sách bài tập Toán 7: Một nhà mạng muốn tìm hiểu loại nhạc chuông của điện thoại di động được người dùng yêu thích, đã lập phiếu khảo sát như hình bên và dự kiến tiến hành thu nhập dữ liệu theo 2 cách sau:
Cách 1: Phát phiếu điều tra cho 100 người tham dự một buổi hoà nhạc thính phòng.
Cách 2: Gửi phiếu điều tra đến 100 người dùng được lựa chọn một cách ngẫu nhiên.
a)Dữ liệu thu được thuộc loại nào?
b)Theo em, dữ liệu thu được trong mỗi cách trên có đại diện cho toàn bộ người dùng dịch vụ của nhà mạng không?

Lời giải
a)
Dữ liệu không phải là số và không thể sắp thứ tự.
b)
Dữ liệu thu được theo cách thứ nhất không có tính đại diện vì chỉ là 100 người tham gia hoà nhạc thính phòng.
Dữ liệu thu được ở cách thứ hai có tính đại diện cho toàn bộ người dùng dịch vụ của nhà mạng vì mang tính ngẫu nhiên.
a)Tìm điều kiện của m và n để biến cố “Lấy được viên bi màu đỏ” có:
b)Giả sử n = 10; m = 5. Tính xác suất để lấy được viên bi màu đỏ.
Phương pháp giải
a)
-Biến cố chắc chắn có xác suất bằng 1
-Biến cố không thể có xác suất bằng 0
b)
Tìm các biến cố đồng khả năng, rồi tính xác suất.
Lời giải
a)
Gọi A : “ Lấy được viên bi màu đỏ”
-Biến cố A có xác suất bằng 1 khi A là biến cố chắc chắn. Khi đó trong hộp đựng toàn viên bi màu đỏ, không có viên bi màu xanh. Vậy n = 0.
-Biến cố A có xác suất bằng 0 khi A là biến cố không thể. Khi đó trong hộp phải không có viên bi màu đỏ, tức là: m = 0.
-Biến cố A có xác suất bằng khi biến cố “Lấy được viên bi màu đỏ” và biến cố “ lấy được viên bi màu xanh” là đồng khả năng. Khi đó m = n.
b)
Đánh số viên bi đỏ là D1; D2;…;D5 và 10 viên bi màu xanh là X1; X2; …; X10.
Xét các biến cố sau:
A: “ Lấy được một trong năm viên bi D1; .. , D5”;
B: “Lấy được một trong năm viên bi X1; …; X5
C: “Lấy được một trong năm viên bi X6; … ; X10”.
Mỗi viên bi có khả năng lấy được như nhau
Do đó, 3 biến cố A, B, C đồng khả năng
Vì luôn xảy ra duy nhất 1 trong 3 biến cố nên xác suất của biến cố A là 1/3.
Vậy xác suất lấy được viên bi màu đỏ là
Xem thêm các bài giải SBT Toán lớp 7 Kết nối với tri thức hay, chi tiết khác:
Bài 2: Công, trừ, nhân, chia số hữu tỉ
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.