Toptailieu.vn giới thiệu Giải bài tập Toán lớp 7 Bài 8: Tính chất ba đường cao của tam giác sách Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7 Tập 2. Mời các bạn đón xem:
Nội dung bài viết
Giải Toán lớp 7 trang 77, 78 Bài 8: Tính chất ba đường cao của tam giác
1. Mục 1
Phương pháp giải:
- Ta dùng êke với cạnh góc vuông đi qua đỉnh B
- Cạnh góc vuông còn lại của êke nằm trùng với AC
Lời giải
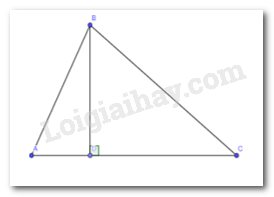
- Ta dùng êke với cạnh góc vuông đi qua đỉnh B
- Cạnh góc vuông còn lại của êke nằm trùng với AC
Thực hành 1 trang 77 Toán lớp 7: Vẽ ba đường cao AH, BK, CE của tam giác nhọn ABC
Phương pháp giải:
- Ta sử dụng thước êke để vẽ đường cao từ các đỉnh
- Ta đặt 1 cạnh góc vuông của êke đi qua 1 đỉnh của tam giác và cạnh góc vuông còn lại của êke trùng với cạnh đối diện với đỉnh đang vẽ .
- Sau đó ta vẽ đường cao của tam giác bằng cạnh góc vuông đi qua đỉnh cần vẽ
Lời giải
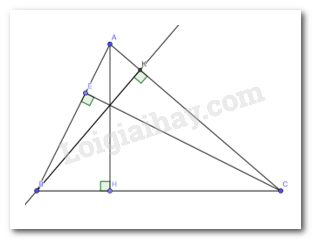
Vận dụng 1 trang 77 Toán lớp 7: Vẽ đường cao xuất phát từ đỉnh B của tam giác vuông ABC (Hình 2a)
Vẽ đường cao xuất phát từ đỉnh F của tam giác tù DEF (Hình 2b
Phương pháp giải:
- Ta sử dụng thước êke để vẽ đường cao từ các đỉnh
- Ta đặt 1 cạnh góc vuông của êke đi qua 1 đỉnh của tam giác và cạnh góc vuông còn lại của êke trùng với cạnh đối diện với đỉnh đang vẽ .
- Sau đó ta vẽ đường cao của tam giác bằng cạnh góc vuông đi qua đỉnh cần vẽ
Lời giải
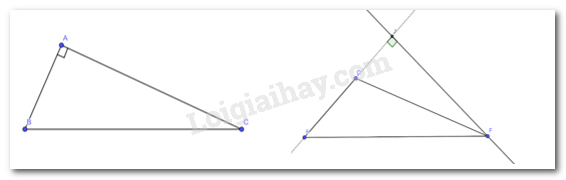
a) Ta thấy ở tam giác ABC vuông tại A thì BA chính là đường cao từ đỉnh B của tam giác vuông ABC
b) Ta thấy đường cao tam giác tù DEF xuất phát từ đỉnh F sẽ nằm ngoài tam giác DEF và chân đường cao nằm trên đoạn kéo dài của đoạn ED.
2. Mục 2
Hoạt động 2 trang 77, 78 Toán lớp 7: Vẽ một tam giác rồi dùng êke vẽ ba đường cao của tam giác ấy (Hình 3). Em hãy quan sát và cho biết các đường cao vừa vẽ có cùng đi qua một điểm hay không.
Phương pháp giải:
- Ta sử dụng êke vẽ 3 đường cao của tam giác
- Sau đó nhận xét về các giao điểm của những đường cao ấy
Lời giải chi tiết:
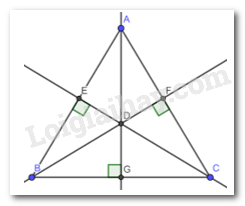
Nhận xét: Các đường cao cùng đi qua 1 điểm
Thực hành 2 trang 77, 78 Toán lớp 7: Cho tam giác LMN có hai đường cao LP và MQ cắt nhau tại S (Hình 6). Chứng minh rằng NS vuông góc với ML.
Phương pháp giải:
- Ta sử dụng định lí 3 đường cao của một tam giác cùng đi qua 1 điểm
Lời giải
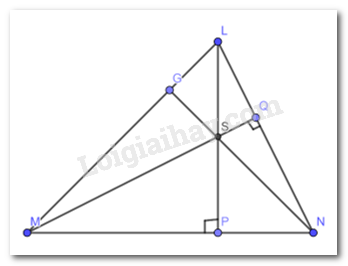
Theo giả thiết ta có : LP và MQ là 2 đường cao của tam giác
Chúng cắt nhau tại S
Theo định lí 3 đường cao trong 1 tam giác cùng đi qua 1 điểm
⇒Đường cao từ đỉnh N cũng đi qua S
⇒NS là đường cao của tam giác MNL
⇒ NS vuông góc với ML tại G (là chân đường cao)
Vận dụng 2 trang 77, 78 Toán lớp 7: Cho tam giác ABC có ba đường cao AD, BE, CF đồng qui tại trực tâm H. Tìm trực tâm của các tam giác HBC, HAB, HAC.
Phương pháp giải:
- Từ các đỉnh ta vẽ các đường cao của tam giác chúng giao nhau ở đâu thì đó là trực tâm
Lời giải
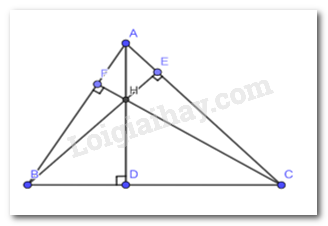
+) Xét tam giác HBC ta có :
HD vuông góc với BC ⇒ HD là đường cao tam giác HBC
BF vuông góc với HC tại F ( kéo dài HC ) ⇒BF là đường cao của tam giác HBC
CE vuông góc với HB tại E ( kéo dài HB ) ⇒CE là đường cao của tam giác HBC
Ta kéo dài HD, BF, CE sẽ cắt nhau tại A
⇒ A là trực tâm tam giác HBC
+) Xét tam giác HAB ta có :
HF vuông góc với AB ⇒ HF là đường cao tam giác HAB
BH vuông góc với AE tại E ( kéo dài HB ) ⇒AE là đường cao của tam giác HAB
BD vuông góc với AH tại D ( kéo dài AH ) ⇒BD là đường cao của tam giác HAB
Ta kéo dài HF, BD, AE sẽ cắt nhau tại C
⇒ C là trực tâm tam giác HAB
+) Xét tam giác HAC ta có :
HE vuông góc với AC ⇒ HE là đường cao tam giác HAC
AF vuông góc với HC tại F ( kéo dài HC ) ⇒AF là đường cao của tam giác HAC
CD vuông góc với AH tại D ( kéo dài AH ) ⇒CD là đường cao của tam giác HAC
Ta kéo dài CD, HE, AF sẽ cắt nhau tại B
⇒ B là trực tâm tam giác HAC.
3. Bài tập
Bài 1 trang 78 Toán lớp 7: Cho tam giác ABC vuông tại A. Lấy điểm H thuộc cạnh AB. Vẽ HM vuông góc với BC tại M. Tia MH cắt tia CA tại N. Chứng minh rằng CH vuông góc với NB.
Phương pháp giải
Ta chứng minh H là trực tâm của tam giác NBC
Lời giải
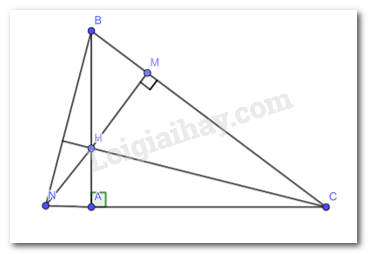
Vì tam giác ABC vuông tại A theo giả thiết nên BA vuông góc với AC
Vì HM cắt AC tại N mà HM vuông góc với BC (giả thiết)
⇒ NM vuông góc với BC tại M
Xét tam giác NBC có NM và BA là 2 đường cao
Mà MN cắt AB tại H nên H là trực tâm của tam giác NBC
⇒ CH đường cao của tam giác NBC (3 đường cao của tam giác đi qua 1 điểm)
⇒ CH vuông góc với NB
Bài 2 trang 78 Toán lớp 7: Cho tam giác ABC vuông tại A. Trên tia BA lấy điểm M sao cho BM = BC. Tia phân giác của góc B cắt AC tại H. Chứng minh rằng MH vuông góc với BC.
Phương pháp giải
- Ta chứng minh H là trực tâm của tam giác AMC
- Từ đó ta chứng minh MH vuông góc với BC
Lời giải
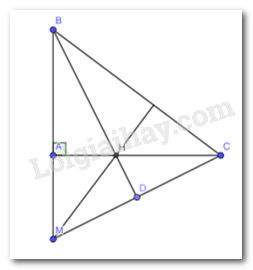
Gọi D giao điểm của tia phân giác của góc B và MC
Xét tam giác BDM và tam giác BDC có :
BD chung
^MBD=^CBD ( BD là phân giác của góc B)
BM = BC ( giả thiết )
( \Rightarrow \Delta BDM=\Delta BDC\)(c.g.c)
⇒^BDM=^BDC(2 góc tương ứng)
Mà 2 góc ở vị trí kề bù ⇒^BDM=^BDC=90o⇒BD⊥CM
Mà AC cắt BD tại H ⇒ H là trực tâm tam giác BMC
⇒ MH là đường cao của tam giác BMC (định lí 3 đường cao đi qua trực tâm tam giác)
⇒ MH vuông góc với BC
Bài 3 trang 78 Toán lớp 7: Cho tam giác ABC vuông cân tại A. Lấy điểm E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AE. Chứng minh rằng:
a) DE vuông góc với BC b) BE vuông góc với DC
Phương pháp giải
- Ta chứng minh vuông góc qua các tam giác vuông cân
- Ta chứng minh E là trực tâm của tam giác BCD
- Từ đó ta chứng minh DE vuông góc với BC và BE vuông góc DC
Lời giải
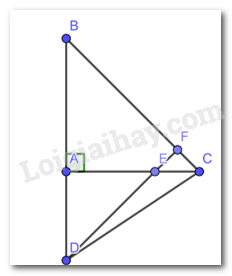
a) Vì tam giác ABC vuông cân tại A
⇒(2 góc ở đáy bằng nhau)
Xét tam giác AED có :
AE = AD
AC vuông góc với AB
⇒Tam giác AED vuông cân tại A
Mà là 2 góc đối đỉnh
Xét tam giác CEF áp dụng định lí tổng 3 góc trong tam giác ta có :
b) Vì DE vuông góc với BC DE là đường cao của tam giác BCD
Vì AC cắt DE tại E nên E là trực tâm tam giác BCD (Do AC cũng là đường cao của tam giác BCD)
BE cùng là đường cao của tam giác BCD (định lí 3 đường cao trong tam giác đi qua trực tâm)
BE vuông góc với DC
Bài 4 trang 78 Toán lớp 7: Cho tam giác nhọn ABC có ba đường cao AB, BE, CF. Biết AD = BE = CF. Chứng minh rằng tam giác ABC đều.
Phương pháp giải
- Ta chứng tam giác BFC = tam giác BEC
- Từ đó suy ra góc B = góc C
- Chứng minh tương tự suy ra được góc A = góc B = góc C
Lời giải
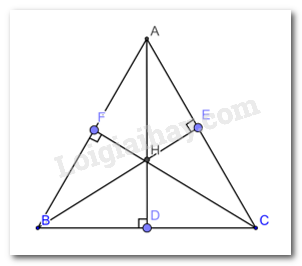
Xét tam giác BFC và tam giác BEC có :
BC chung
FC = BE
( cạnh huyền – cạnh góc vuông)
⇒
( 2 góc tương ứng ) (1)
Xét tam giác CFA và tam giác ADC ta có :
CF = AD
AC chung
(cạnh huyền – cạnh góc vuông)
(2 góc tương ứng ) (2)
Từ (1) và (2)
Tam giác ABC là tam giác đều do có 3 góc bằng nhau
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.