Toptailieu.vn giới thiệu Giải bài tập Toán lớp 7 Bài 7: Tính chất ba đường trung tuyến của tam giác sách Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7 Tập 2. Mời các bạn đón xem:
Nội dung bài viết
Giải Toán lớp 7 trang 73, 74, 75, 76 Bài 7: Tính chất ba đường trung tuyến của tam giác
1. Mục 1
Phương pháp giải:
Vẽ theo yêu cầu đề bài
Lời giải
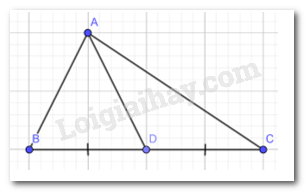
Phương pháp giải:
- Xác định các trung điểm của các cạnh tam giác và vẽ các đường trung tuyến
Lời giải
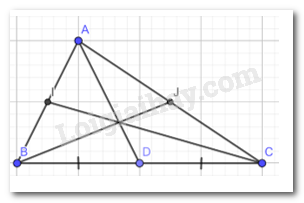
Vận dụng 1 trang 73 Toán lớp 7:
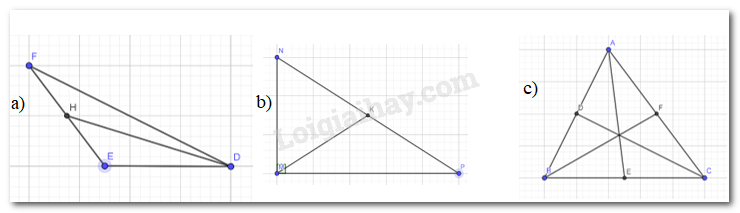
a) Vẽ đường trung tuyến DH của tam giác DEF (Hình 2).
b) Vẽ đường trung tuyến MK của tam giác MNP (Hình 3).
c) Vẽ tam giác nhọn IJK và tất cả các đường trung tuyến của nó.
Phương pháp giải:
- Xác định các trung điểm và vẽ các trung tuyến
Lời giải
2. Mục 2
Hoạt động 2 trang 74, 75 Toán lớp 7:
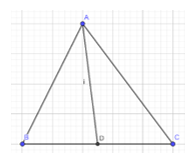
a) Cắt một tam giác bằng giấy. Gấp lại để xác định trung điểm một cạnh của nó. Kẻ đoạn thẳng nối trung điểm này với đỉnh đối diện (Hình 4). Bằng cách tương tự, hãy vẽ tiếp hai đường trung tuyến còn lại.
Quan sát tam giác trên hình, em thấy ba đường trung tuyến vừa vẽ có cùng đi qua một điểm hay không.
b) Em hãy đếm ô rồi vẽ lại tam giác ABC trong Hình 5 vào giấy kẻ ô vuông. Vẽ hai đường trung tuyến BE và CF của tam giác ABC. Hai đường trung tuyến này cắt nhau tại G. Tia AG cắt BC tại D.
Em hãy quan sát vào cho biết:
- AD có phải đường trung tuyến của tam giác ABC hay không?
- Các tỉ số BGBEBGBE, CGCFCGCF, AGADAGAD bằng bao nhiêu ?
Lời giải
a)- Ta xác định trung điểm 1 cạnh bằng cách gấp sao cho 2 đỉnh của tam giác trùng nhau, khi đó giao của nét gấp đi qua 1 cạnh của tam giác sẽ là trung điểm của cạnh đó
- Rồi từ các trung điểm vừa xác định được ta kẻ các đường trung tuyến của tam giác từ các đỉnh
- Nhận xét : Ta thấy 3 đường trung tuyến trong tam giác này đều sẽ đi qua 1 điểm
b)
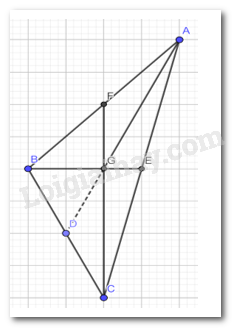
- Ta nối dài đoạn AG sao cho AG cắt BC tại 1 điểm
- Ta thấy điểm giao nhau giữa AG và BC chính là trung điểm của BC
- Nên AG là trung tuyến của tam giác ABC
- Ta sẽ sử dụng số đo dựa trên các ô để xét tỉ số giữa các đoạn thẳng
BGBE=23;CGCF=46;AGAD=4.46.6BGBE=23;CGCF=46;AGAD=4.46.6
- Ta thấy sau khi rút gọn các tỉ số ta có :
BGBE=CGCF=AGAD=23BGBE=CGCF=AGAD=23
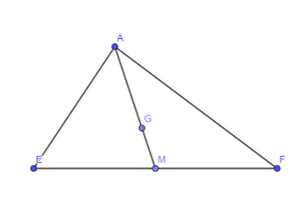
Hãy tính các tỉ số:
a) GMAMGMAM
b) GMAGGMAG
c) AGGMAGGM
Phương pháp giải:
- Ta dựa vào định lí ba đường trung tuyến cắt nhau tại 1 điểm. Điểm đó cách mỗi đỉnh một khoảng bằng 2323độ dài trung tuyến đi qua đỉnh ấy
Lời giải
a) Vì G là trọng tâm của tam giác AEF với đường trung tuyến AM nên theo định lí 3 đường trung tuyến cắt nhau tại trọng tâm ta có :
AGAM=23AGAM=23⇒GMAM=1−23=13⇒GMAM=1−23=13
b) Vì AGAM=23AGAM=23 và GMAM=13GMAM=13(theo câu a)
⇒GMAG=12⇒GMAG=12
c) Vì GMAG=12GMAG=12(chứng minh b)
⇒AGGM=2⇒AGGM=2
Vận dụng 2 trang 74, 75 Toán lớp 7: Cho tam giác ABC có O là trung điểm của BC, trên tia đối của tia OA, lấy điểm D sao cho OA = OD. Gọi I và J lần lượt là trọng tâm của các tam giác ABC và BCD. Chứng minh rằng AI = IJ = JD.
Phương pháp giải:
- Ta dựa vào định lí ba đường trung tuyến cắt nhau tại 1 điểm. Điểm đó cách mỗi đỉnh một khoảng bằng 2323độ dài trung tuyến đi qua đỉnh ấy .
- Ta sẽ chứng minh AI = IJ = JD = 2323AO = 2323OD
Lời giải
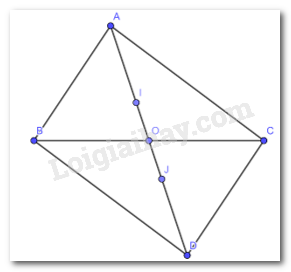
Vì I là trọng tâm tam giác ABC theo giả thiết nên ta có
AI=23AO=2IOAI=23AO=2IO(định lí về trọng tâm trong tam giác)
Tương tự J là trọng tâm tam giác BCD nên ta có :
DJ=23OD=2OJDJ=23OD=2OJ (định lí về trọng tâm trong tam giác)
Mà OA = OD (giả thiết)
⇒AI=DJ=23OA=23OD=2OI=2OJ⇒AI=DJ=23OA=23OD=2OI=2OJ
Mà OI = OJ do cùng =13OA=13OD=13OA=13OD(tính chất trọng tâm trong tam giác)
⇒2OI=2OJ=213AO=213OD=IJ⇒2OI=2OJ=213AO=213OD=IJ
⇒AI=DJ=IJ=23OA=23OD⇒AI=DJ=IJ=23OA=23OD(điều phải chứng minh)
3. Bài tập
Bài 1 trang 75 Toán lớp 7: Quan sát Hình 8.
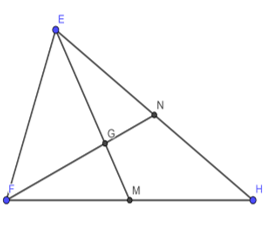
Tìm số thích hợp để ghi vào chỗ chấm trong các đẳng thức sau:
EG=...EM;GM=...EM;GM=...EGFG=...GN;FN=...GN;FN=...FG
Phương pháp giải
- Ta dựa vào định lí ba đường trung tuyến cắt nhau tại 1 điểm. Điểm đó cách mỗi đỉnh một khoảng bằng 23 độ dài trung tuyến đi qua đỉnh ấy .
Lời giải
EG=23EM;GM=13EM;GM=12EGFG=2GN;FN=3GN;FN=32FG
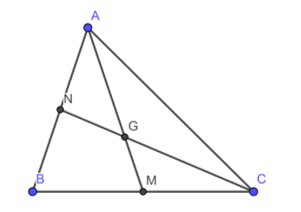
Bài 2 trang 75 Toán lớp 7: Quan sát Hình 9
a) Biết AM = 15 cm, tính AG
b) Biết GN = 6 cm, tính CN
Phương pháp giải
- Ta dựa vào định lí ba đường trung tuyến cắt nhau tại 1 điểm. Điểm đó cách mỗi đỉnh một khoảng bằng 23độ dài trung tuyến đi qua đỉnh ấy
- Ta áp dụng các tỉ lệ giữa các đoạn thẳng và độ dài của chúng
Lời giải
a) Theo đề bài ta có AM = 15 cm
Mà CN và AM là 2 trung tuyến của tam giác ABC
AM cắt CN tại G nên G là trọng tâm tam giác ABC
⇒AG=23AM(định lí về trọng tâm tam giác)
⇒AG=2315cm=10cm
b) Vì G là trọng tâm tam giác ABC
⇒CG=23CN(theo tính chất của trung tuyến đi qua trọng tâm)
Mà CG+GN=CN nên ta có GN=CN−CG=CN−23CN=13CN
Theo giả thiết GN = 6cm ta có
⇒CN=3GN=3.6cm=18cm
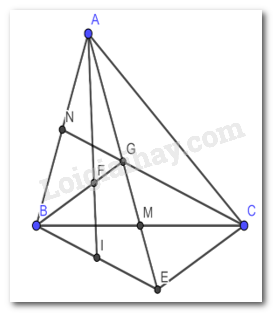
Bài 3 trang 75 Toán lớp 7: Cho tam giác ABC. Hai đường trung tuyến AM và CN cắt nhau tại G. Trên tia đối của tia AM lấy điểm E sao cho ME = MG.
a) Chứng minh rằng BG song song với EC.
b) Gọi I là trung điểm của BE, AI cắt BG tại F. Chứng minh rằng AF = 2FI
Phương pháp giải
- Ta dựa vào định lí ba đường trung tuyến cắt nhau tại 1 điểm. Điểm đó cách mỗi đỉnh một khoảng bằng 23độ dài trung tuyến đi qua đỉnh ấy
- Câu a ta sẽ chứng minh 2 góc so le trong bằng nhau thông qua các tam giác bằng nhau
- Câu b ta sẽ chứng minh F là trọng tâm tam giác ABE
Lời giải
a) Xét tam giác BGM và tam giác CEM có :
^GMB=^EMC(2 góc đối đỉnh)
GM = ME (do G đối xứng E qua M)
MB = MC (do M là trung điểm của BC)
⇒ΔBGM=ΔCEM(c−g−c)
⇒^GBM=^MCE(2 góc tương ứng bằng nhau)
Mà 2 góc trên ở vị trí so le trong nên BG⫽CE
b) Vì I là trung điểm BE nên AI sẽ là trung tuyến của tam giác ABE
Và BG cũng là trung tuyến của tam giác ABE do G là trung điểm AE
Vì BG cắt AI tại F nên F sẽ là trọng tâm của tam giác ABE
⇒AF=23AI(định lí về trọng tâm tam giác)
Mà AI = AF + FI ⇒ FI = AI – AF
⇒FI=AI−23AI=13AI
⇒2FI=AF=23AI
⇒ AF = 2 FI
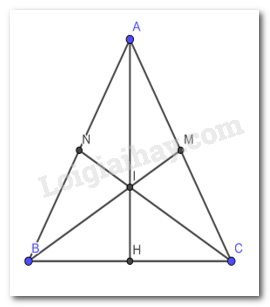
Bài 4 trang 75 Toán lớp 7: Cho tam giác ABC cân tại A có BM và CN là hai đường trung tuyến.
a) Chứng minh rằng BM = CN
b) Gọi I là giao điểm của BM và CN, đường thẳng AI cắt BC tại H. Chứng minh H là trung điểm của BC
Phương pháp giải
- Ta chứng minh 2 tam giác bằng nhau để từ đó chứng minh 2 đoạn thẳng bằng nhau
- Ta chứng minh I là trọng tâm tam giác ABC và chứng minh AH là trung tuyến của tam giác ABC và H là trung điểm của BC
Lời giải
a) Vì tam giác ABC cân tại A theo giả thiết. BM và CN là 2 đường trung tuyến nên M, N là 2 trung điểm của AC, AB.
Vì AB = AC (tính chất tam giác cân)
⇒AB2=AC2=AN=AM
Xét tam giác AMB và tam giác ANC ta có :
AM = AN (cmt)
AB = AC
Góc A chung
⇒ΔAMB=ΔANC
⇒BM=CN ( 2 cạnh tương ứng )
b) Vì BM và CN là các đường trung tuyến
Mà I là giao điểm của BM và CN
⇒ I là trọng tâm của tam giác ABC
⇒ AI là đường trung tuyến của tam giác ABC hay AH đường là trung tuyến của tam giác ABC
⇒ H là trung điểm của BC
Phương pháp giải
- Ta chứng minh AB = AC bằng cách chứng minh 2 tam giác bằng nhau
Lời giải
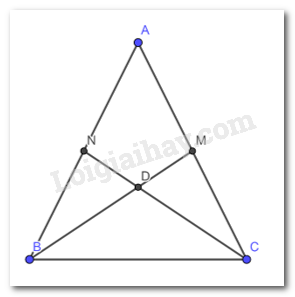
Gọi D là giao điểm của CN và BM
⇒ D là trọng tâm tam giác ABC
⇒CD=23CN=BD=23BM ( do BM = CN )
⇒ tam giác DBC cân tại D do BD = CD
⇒ ^DBC=^DCB(2 góc đáy trong tam giác cân) (1)
Xét ΔNDB và ΔMDC có :
BD = CD
^NDB=^MDC (2 góc đối đỉnh)
ND = DM (do cùng =13CN=13BM (tính chất của trung trực đi qua trọng tâm tam giác ))
⇒ΔNDB=ΔMDC (c.g.c)
⇒^NBD=^MCD(2 góc tương ứng) (2)
Từ (1) và (2) ⇒^ABC=^ACB do ^ABC=^NBD+^DBC và ^ACB=^MCD+^DCB
⇒ΔABC cân tại A (do 2 góc bằng nhau)
Bài 6 trang 76 Toán lớp 7: Cho tam giác ABC cân tại A có BD và CE là hai đường trung tuyến cắt nhau tại F (Hình 10). Biết BE = 9 cm, tính độ dài đoạn thẳng DF.
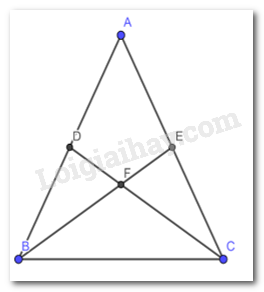
Phương pháp giải
- Ta chứng minh F là trọng tâm tam giác ABC
- Sau đó chứng minh CD = BE
- Áp dụng định lí về trọng tâm tam giác ta tính các đoạn DF, EF
Lời giải
Vì BE, CD là 2 trung tuyến của tam giác ABC
NÊn E, D lần lượt là trung tuyến của AB và AC
⇒AD=AE=12AB=12AC
Xét tam giác ADC và tam giác AEB có :
AD = AE
Góc A chung
AB = AC (tam giác ABC cân tại A theo giả thiết)
⇒ΔADC=ΔAEB(c−g−c)
⇒BE=CD(cạnh tương ứng)
Vì F là giao 2 trung tuyến nên F là trọng tâm tam giác ABC
⇒CF=BF=23BE=23CD ( định lí về trung tuyến đi qua trọng tâm tam giác )
⇒13BE=13CD⇒DF=FE=13.9cm=3cm
⇒ DF = 3 cm
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.