Toptailieu biên soạn và giới thiệu giải sách bài tập Tin học 10 trang 12,13 Bài 5: Dữ liệu lôgic Sách bài tập Tin học 10 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Tin học 10 Bài 5.
Nội dung bài viết
Sách bài tập Tin học 10 Bài 5 (Kết nối tri thức): Dữ liệu lôgic
Câu 5.1 trang 12 SBT Tin học 10: Em hãy điền vào ô trống trong bảng theo dõi sau:
a)
|
An giỏi |
An chăm chỉ |
An giỏi VÀ chăm chỉ |
Ý nghĩa |
|
Sai |
Sai |
Sai |
Đã kém lại lười |
|
Sai |
Đúng |
|
|
|
Đúng |
Sai |
|
|
|
Đúng |
Đúng |
|
|
b) Ở các trường đại học, sinh viên giỏi hoặc gia đình nghèo sẽ được cấp học bổng. Em hãy tính giá trị điều kiện được cấp học bổng.
|
Học giỏi |
Nghèo |
Học giỏi HOẶC nghèo |
Ý nghĩa |
|
Sai |
Sai |
Sai |
Không đủ tiêu chuẩn |
|
Sai |
Đúng |
|
|
|
Đúng |
Sai |
|
|
|
Đúng |
Đúng |
|
|
Lời giải:
a)
|
An giỏi |
An chăm chỉ |
An giỏi và chăm chỉ |
Ý nghĩa |
|
Sai |
Sai |
Sai |
Đã kém lại lười |
|
Sai |
Đúng |
Sai |
Không giỏi nhưng chăm chỉ |
|
Đúng |
Sai |
Sai |
Giỏi nhưng lười |
|
Đúng |
Đúng |
Đúng |
Vừa giỏi vừa chăm chỉ |
b)
|
Học giỏi |
Nghèo |
Học giỏi HOẶC nghèo |
Ý nghĩa |
|
Sai |
Sai |
Sai |
Không đủ tiêu chuẩn |
|
Sai |
Đúng |
Đúng |
Đủ tiêu chuẩn |
|
Đúng |
Sai |
Đúng |
Đủ tiêu chuẩn |
|
Đúng |
Đúng |
Đúng |
Đủ tiêu chuẩn
|
Em hãy tìm thêm ba ví dụ khác.
Lời giải:
- Ảnh màu /ảnh đen trắng.
- Đèn bật /tắt.
- Tài liệu bản chính /bản sao.
Em hãy viết biểu thức lôgic tương ứng với các Hình 5.1b, Hình 5.1c, Hình 5.1d.
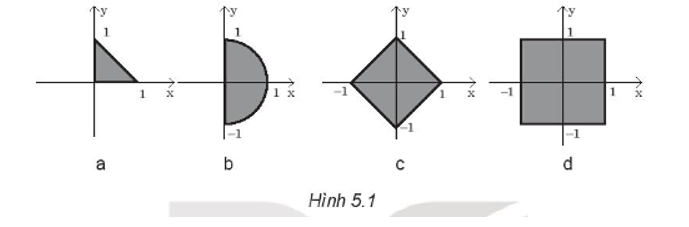
Lời giải:
Hình 5.1b) Biểu thức logic là:![]()
Hình 5.1c) Biểu thức logic là:![]()
Hình 5.1d) Biểu thức logic là:![]()
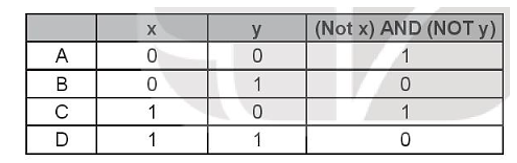
Lời giải:
Kết quả đáp án C sai vì:
x = 1, y = 0 ⇒ Not x = 0, Not y = 1
⇒ (Not x) AND (Not y) = 0 AND 1 = 0
Lời giải:
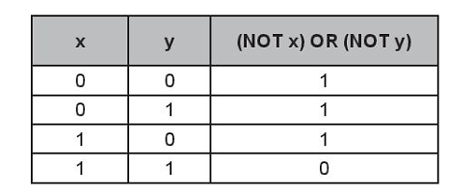
Câu 5.6 trang 13 SBT Tin học 10: Đố vui (Bài toán đoán màu mũ).
Chuyện rằng có 10 nhà thông thái (rất giỏi về suy luận logic) bị bọn cướp biển bắt được và giam trên đảo hoang. Chúng bịt mắt họ lại và đội lên đầu họ một chiếc mũ (đỏ hoặc xanh), sau đó bỏ bằng bịt mắt. Mỗi người sẽ nhìn thấy và biết màu mũ của tất cả những người khác nhưng không biết màu mũ của mình. Bọn cướp ra luật chơi, chúng sẽ hỏi từng người xem họ đội mũ màu gì. Với điều kiện họ không được trao đổi với nhau, không được đoán mò, nếu chỉ một người đoán đúng, có cơ sở thì chúng sẽ tha tất, ngược lại sẽ tử hình toàn bộ.
Chúng hỏi nhà thông thái thứ nhất, ông nhìn tất cả những người còn lại và bảo không biết, không đủ cơ sở để biết màu mũ của mình. Chúng lại hỏi thông thái thứ hai, anh ta cũng trả lời không đủ cơ sở để biết màu mũ của mình.
Lần lượt cả 9 nhà thông thái đều trả lời rằng không đủ cơ sở để biết màu mũ của mình.
Đến nhà thông thái thứ mười, ông nói ngay màu mũ của mình và giải thích cách suy luận. Bọn cướp khâm phục và thả tất cả các nhà thông thái.
Em có biết nhà thông thái thứ 10 đã suy luận như thế nào không?
Lời giải:
Bài toán đoán màu mũ.
Gọi ai là mệnh đề "Các nhà thông thái (NTT) từ thứ i đến thứ 10 có cùng màu mũ".
Theo giả thiết, có hai loại mũ nên đi sai.
NTT 1 không đoán được nên a2 cũng sai vì ngược lại, nếu NTT từ thứ 2 đến thứ 10 cùng một màu mũ thì NTT thứ nhất sẽ biết ngay là mình có màu mũ ngược lại. Tất cả mọi NTT đều biết điều này.
NTT 2 biết điều này mà cũng không đoán được điều đó chứng tỏ a3 cũng sai.
Tất cả mọi NTT đều biết điều này.
Cứ như vậy ta sẽ thấy tất cả a1, a2, a3, … đến a9 đều sai, tức là màu mũ của NTT 9 và 10 là khác nhau. Vì vậy đến lượt mình, NTT 10 nhìn vào màu mũ của NTT 9 và bảo màu mũ của mình là màu ngược lại.
Xem thêm lời giải vở bài tập Tin học lớp 10 Kết nối tri thức hay, chi tiết khác:
Bài 4: Hệ nhị phân và dữ liệu số nguyên
Bài 6: Dữ liệu âm thanh và hình ảnh
Bài 7: Thực hành sử dụng thiết bị số thông dụng
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.