Với Giải SBT Tin học 10 trang 65 trong Bài 31: Thực hành viết chương trình đơn giản Sách bài tập Tin học 10 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Tin học 10.

SBT Tin học 10 trang 65 Kết nối tri thức

Câu 31.5 trang 65 SBT Tin học 10: Em hãy viết chương trình nhập một xâu kí tự bất kì từ bàn phím. Cần sắp xếp lại các chữ số thì dồn sang trái, các chữ cái tiếng Anh thì dồn sang phải xâu, các kí tự khác thì giữ nguyên vị trí.

Lời giải:

Hướng dẫn:

Chúng ta đã biết giữa các kí tự cũng có thể được so sánh. Hai kí tự ch1 và ch2 được so sánh với nhau thông qua vị trí của các kí tự này trong bảng mã ASCII hoặc Unicode. Quan hệ so sánh tự nhiên giữa các kí tự chữ cái và số như sau:

"0" < "1" < ... < "9".

"A" < "B" < ... < "Z" < "a" < "b" <...< "Z".

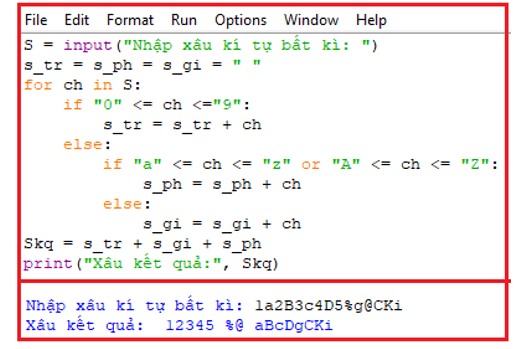
Để giải bài tập này chúng ta cần tạo các biến nhớ dùng để lưu các xâu kí tự trung gian là s_tr (xâu dùng để lưu tạm các kí tự là số), s_ph (xâu dùng để lưu tạm các kí tự là chữ cái) và s_gi (xâu dùng để lưu các kí tự không là chữ số cũng không là chữ cái). Thuật toán của chương trình như sau: duyệt một lần tất cả các kí tự của xâu gốc S, sau đó đưa các kí tự này vào các xâu trung gian s­_tr, s_ph, s_gi. Xâu kết quả sẽ là s_tr + s_gi + s_ph. Mở phần mềm soạn thảo và nhập chương trình sau:

S = input("Nhập xâu kí tự bất kì: ")

s_tr = s_ph = s_gi = " "

for ch in S:

 if "0" <= ch <="9":

  s_tr = s_tr + ch

 else:

  if "a" <= ch <= "z" or "A" <= ch <= "Z":

   s_ph = s_ph + ch

  else:

   s_gi = s_gi + ch

Skq = s_tr + s_gi + s_ph

print("Xâu kết quả:", Skq)

* Chương trình chạy thử:

Câu 31.6 trang 65 SBT Tin học 10: Em hãy viết chương trình nhập số tự nhiên n, sau đó nhập n họ tên đầy đủ học sinh trong lớp. Khi kết thúc sẽ in ra danh sách học sinh với 2 cột, cột 1 là tên, cột 2 là họ đệm của học sinh này.

Lời giải:

Hướng dẫn:

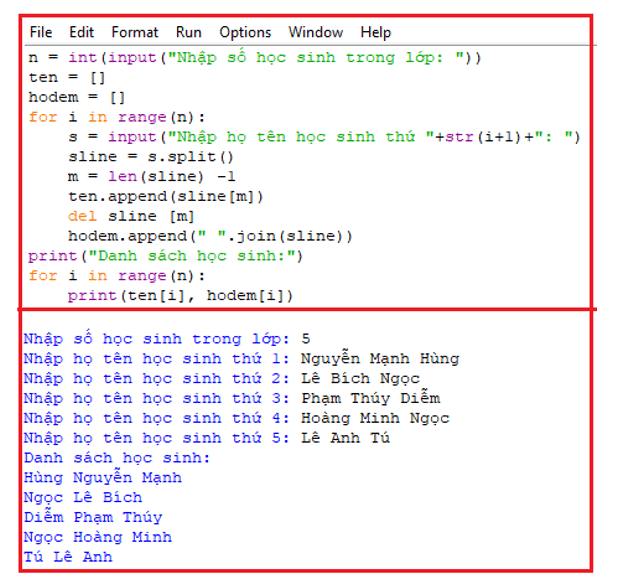
Mỗi họ tên được nhập sẽ được tách ra thành tên và họ đệm bằng hàm split(). Các tên học sinh sẽ được đưa vào dãy ten, các họ đệm sẽ được đưa vào dãy hodem. Sau khi nhập xong thì in ra danh sách các tên và họ đệm này.

n = int(input("Nhập số học sinh trong lớp: "))

ten = []

hodem = []

for i in range(n):

 s = input("Nhập họ tên học sinh thứ "+str(i+1)+": ")

 sline = s.split()

 m = len(sline) -1

 ten.append(sline[m])

 del sline [m]

 hodem.append(" ".join(sline))

print("Danh sách học sinh:")

for i in range(n):

 print(ten[i], hodem[i])

* Chương trình chạy thử:

Câu 31.7 trang 65 SBT Tin học 10: Em hãy viết chương trình nhập hai số tự nhiên Y1, Y2 là số năm, Y2 > Y1. Tính xem trong khoảng thời gian từ năm Y1 đến năm Y2 có bao nhiêu năm nhuận. Áp dụng tính xem trong thế kỉ XXI có bao nhiêu năm nhuận.

Lời giải:

Chương trình có thể viết như sau:

def nhuan(year):

 if year % 400 == 0 or (year % 4 == 0 and year%100 != 0):

  return True

 else:

  return False

def Tinh_nhuan(Y1, Y2):

 count = 0

 for year in range(Y1, Y2+1):

  if nhuan (year): count = count + 1

 return count

Y1 = int(input("Nhập năm đầu: "))

Y2 = int(input("Nhập năm cuối: "))

print("Từ năm ",Y1," đến năm ",Y2," có ",Tinh_nhuan(Y1, Y2)," năm nhuận.")

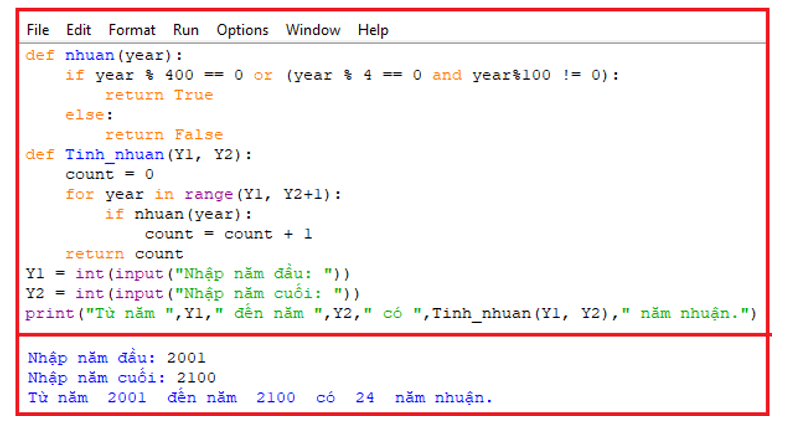
* Chương trình chạy thử tính năm nhuận của thế kỉ XXI như sau:

Câu 31.8 trang 65 SBT Tin học 10: Gọi ƯCLN(a, b) là hàm ƯCLN của hai số tự nhiên a, b. Dễ thấy ta có ƯCLN(a, b) = ƯCLN(b, a%b) nếu b > 0 và ƯCLN(a, 0) = a. Từ đó hãy viết chương trình nhập hai số a, b và tính ƯCLN của a và b.

Lời giải:

Chương trình có thể viết như sau:

def UCLN(a, b):

 while b > 0:

  r = a%b

  a = b

  b = r

 return a

a,b = eval(input("Nhập hai số a, b cách nhau bởi dấu phẩy: "))

print("ƯCLN là: ", UCLN(a,b))

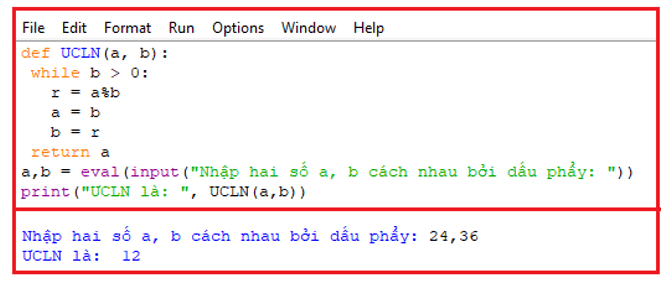
* Chương trình chạy thử với bộ test (a,b) = (24,36)

Câu 31.9 trang 65 SBT Tin học 10: Em hãy viết chương trình nhập số tự nhiên n > 1, sau đó in ra tất cả các ước số nguyên tố khác nhau của n theo hàng ngang trên màn hình. Ví dụ:

- Nếu n = 10 thì in ra 2 5.

- Nếu n = 12 thì in ra 2 3.

Lời giải:

Hướng dẫn:

Lưu ý đến yêu cầu của bài toán là không in tất cả các ước nguyên tố trong khai triển n thành tích các thừa số nguyên tố, mà chỉ in mỗi ước số nguyên tố một lần. Vì vậy nếu đã tìm ra được một ước nguyên tố k của n thì cần giảm n bằng cách chia n cho k cho đến khi không chia hết được nữa thì tìm tiếp sang số tiếp theo.

Chương trình có thể viết như sau:

n = int(input("Nhập số tự nhiên n: "))

print(n,":", end = " ")

k = 2

while n > 1:

 while k < n and n%k != 0:

  k = k +1

 if k<=n and n%k == 0:

  print(k, end = " ")

  while n%k == 0:

   n = n//k

Câu 31.10 trang 65 SBT Tin học 10: Bài toán tìm tổng con lớn nhất.

Giả sử một công ty du lịch đã thiết kế một chương trình du lịch cố định đi qua lần lượt n địa điểm. Mỗi khách hàng lại có các đánh giá khác nhau cho mỗi địa điểm này. Giả sử khách hàng tên An đã đánh giá các địa điểm trong chương trình du lịch theo dãy các giá trị: A[0], A[1], ..., A[n - 1]

Công ty muốn sắp sắp cho khách hàng An đi một phần của chương trình du lịch bằng cách đi theo một dãy con liên tục các địa điểm, ví dụ:

i, i + 1, i + 2, ..., j

Mục đích của việc chọn chương trình cho khách hàng An là làm sao cho tổng giá trị:

A[i] + A[i + 1] + ... + A[j]         (1) là lớn nhất có thể.

Cho trước dãy các đánh giá n địa điểm của chương trình du lịch, hãy thiết kế một chương trình du lịch con cho khách hàng sao cho tổng (1) là lớn nhất.

Ví dụ nêu dãy các đánh giá là: 1, 7, -5, -9, 3, -1,10, -6, 5

thì chương trình du lịch con đi qua các địa điểm với đánh giá 3, -1, 10 có tổng lớn nhất tức là làm khách hàng hài lòng nhất.

Lời giải:

Hướng dẫn:

Gọi S(i, j) = A[i] + A[i + 1] + ... + A[j]

Khi đó bài toán đặt ra là cần tìm i, j sao cho giá trị S(i, j) lớn nhất. Từ đó suy ra lời giải đơn giản sau:

A = [1,7,-5,-9,3,-1,10,-6, 5]

n = len(A)

imax = 0

jmax = 0

Smax = A[0]

for i in range(n):

 S = 0

 for j in range(i,n):

  S = S + A[j]

  if S > Smax:

   imax = i

   jmax = j

   Smax = S

print("Chương trình du lịch tối ưu là:")

print(imax, jmax)

for i in range(imax, jmax+1):

 print (A[i], end = " ")