Giải Toán 8 trang 59 Tập 1 (Chân trời sáng tạo)

Ngọc Nguyễn Ngày: 29-02-2024 Lớp 8

249

Với giải SGK Toán 8 Chân trời sáng tạo trang 59 chi tiết trong Bài 1: Định lí Pythagore giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Giải Toán 8 trang 59 Tập 1 (Chân trời sáng tạo)

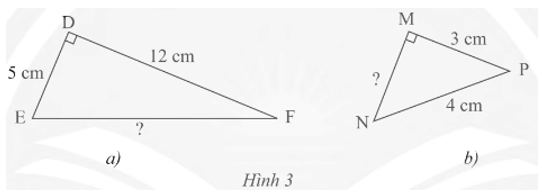
Thực hành 1 trang 59 Toán 8 Tập 1: Tính độ dài cạnh EF, MN của các tam giác vuông trong Hình 3.

Toán 8 Bài 1 (Chân trời sáng tạo): Định lí Pythagore (ảnh 3)

Lời giải:

Hình 3a: Áp dụng định lí Pythagore vào tam giác vuông DEF có cạnh huyền EF, ta có:

EF² = DE² + DF²

Suy ra EF² = 5² + 12² = 25 + 144 = 169 = 13².

Vậy EF = 13 cm.

Hình 3b: Áp dụng định lí Pythagore vào tam giác vuông MNP có cạnh huyền NP, ta có:

NP² = MN² + MP²

Suy ra MN² = NP² – MP²

MN² = 4² – 3² = 16 – 9 = 7.

Vậy EF = $\sqrt{7}$ cm.

Vận dụng 1 trang 59 Toán 8 Tập 1: Một chiếc ti vi màn hình phẳng có chiều rộng và chiều dài đo được lần lượt là 72 cm và 120 cm. Tính độ dài đường chéo của màn hình chiếc ti vi đó theo đơn vị inch (biết 1 inch ≈ 2,54 cm).

Toán 8 Bài 1 (Chân trời sáng tạo): Định lí Pythagore (ảnh 4)

Lời giải:

Chiếc ti vi ở Hình 4 được mô tả bởi tam giác ABC vuông tại A có các kích thước như hình vẽ sau:

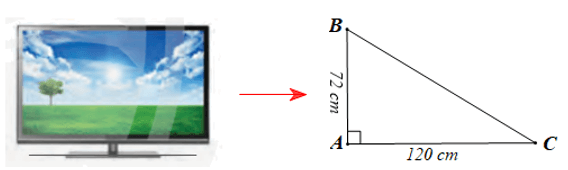
Toán 8 Bài 1 (Chân trời sáng tạo): Định lí Pythagore (ảnh 5)

Áp dụng định lí Pythagore vào tam giác ABC có cạnh huyền BC, ta có:

BC² = AB² + AC² = 72² + 120² = 5 184 + 14 400 = 19 584.

Suy ra BC = $24 \sqrt{34}$ (cm).

Vậy độ dài đường chéo của màn hình chiếc ti vi đó theo đơn vị inch là:

$24 \sqrt{34} : 2, 54 \approx 55$ (inch).

2. Định lý Pythagore đảo

Khám phá 2 trang 59 Toán 8 Tập 1: Vẽ vào vở tam giác ABC có AB = 12 cm, AC = 5 cm, BC = 13 cm, rồi xác định số đo $\hat{B A C}$ bằng thước đo góc

Lời giải:

Ta vẽ tam giác ABC có AB = 12 cm, AC = 5 cm, BC = 13 cm như sau:

• Vẽ đoạn thẳng AB = 12 cm;

• Vẽ cung tròn tâm A bán kính 5 cm và cung tròn tâm B bán kính 13 cm. Hai cung tròn này cắt nhau tại một điểm, điểm này là điểm C.

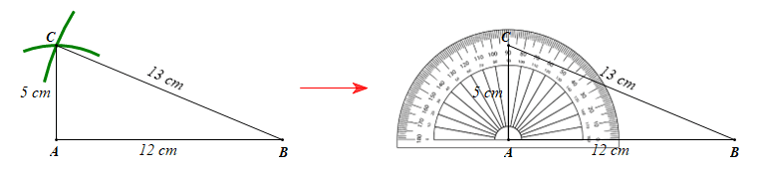
Toán 8 Bài 1 (Chân trời sáng tạo): Định lí Pythagore (ảnh 6)

Dùng thước đo góc (đặt thước như hình vẽ trên) ta xác định được $\hat{B A C} = 90 °$ .

Xem thêm các bài giải SGK Toán 8 Chân trời sáng tạo hay, chi tiết khác:

Khởi động trang 58 Toán 8 Tập 1: Hãy so sánh diện tích hình vuông màu xanh với tổng diện tích của hai hình vuông màu đỏ và màu vàng.

Khám phá 1 trang 58 Toán 8 Tập 1: Cho một tam giác vuông có hai cạnh góc vuông là a, b và cạnh huyền là c.

Thực hành 1 trang 59 Toán 8 Tập 1: Tính độ dài cạnh EF, MN của các tam giác vuông trong Hình 3.

Khám phá 2 trang 59 Toán 8 Tập 1: Vẽ vào vở tam giác ABC có AB = 12 cm, AC = 5 cm, BC = 13 cm, rồi xác định số đo bằng thước đo góc

Thực hành 2 trang 60 Toán 8 Tập 1: Tìm tam giác vuông trong các tam giác sau:

Vận dụng 2 trang 60 Toán 8 Tập 1: a) Nam dự định làm một cái êke từ ba thanh nẹp gỗ. Nam đã có hai thanh làm hai cạnh góc vuông dài 6 cm và 8 cm. Hỏi thanh nẹp còn lại Nam phải làm có độ dài bao nhiêu? (Giả sử các mối nối không đáng kể)

Thực hành 3 trang 61 Toán 8 Tập 1: Tính các độ dài PN và BC trong Hình 9.

Vận dụng 3 trang 61 Toán 8 Tập 1: Tính chiều dài cần cẩu AB trong Hình 10.

Bài 1 trang 61 Toán 8 Tập 1: Cho tam giác ABC vuông tại A.

Bài 2 trang 62 Toán 8 Tập 1: Tính độ cao của con diều so với mặt đất (Hình 11).

Bài 3 trang 62 Toán 8 Tập 1: Lần lượt tính độ dài các cạnh huyền a, b, c, d của các tam giác vuông trong Hình 12. Hãy dự đoán kết quả của các cạnh huyền còn lại.

Bài 4 trang 62 Toán 8 Tập 1: Chứng minh rằng tam giác ABC vuông trong các trường hợp sau:

Bài 5 trang 62 Toán 8 Tập 1: Cho biết thang của một xe cứu hoả có chiều dài 13 m, chân thang cách mặt đất 3 m và cách tường của toà nhà 5 m. Tính chiều cao mà thang có thể vươn tới.

Bài 6 trang 62 Toán 8 Tập 1: Một con thuyền đang neo ở một điểm cách chân tháp hải đăng 180 m. Cho biết tháp hải đăng cao 25 m. Hãy tính khoảng cách từ thuyền đến ngọn hải đăng.

Xem thêm các bài giải SGK Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Diện tích xung quanh và thể tích của hình chóp tam giác đều, hình chóp tứ giác đều

Bài tập cuối chương 2

Bài 2: Tứ giác

Bài 3: Hình thang – Hình thang cân

Bài 4: Hình bình hành – Hình thoi

Từ khóa :

Giải bài tập Toán 8

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương