Toptailieu biên soạn và giới thiệu giải Sách bài tập Toán 8 Bài 1: Định lí Pythagore sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 8 Bài 1.

SBT Toán 8 (Chân trời sáng tạo) Bài 1: Định lí Pythagore

Bài tập trang 52 sách bài tập Toán 8 Tập 1

Bài 1 trang 52 sách bài tập Toán 8 Tập 1: Cho tam giác MNP vuông tại M.

a) Tính độ dài cạnh NP nếu biết MN = 7, MP = 24.

b) Tính độ dài cạnh MP nếu biết NP = 29, MN = 20.

c) Tính độ dài cạnh MN nếu biết NP = 61, MP = 11.

Lời giải:

a) Áp dụng định lý Pythagore vào tam giác MNP vuông tại M, ta có:

NP² = MN² + MP² = 7² + 24² = 49 + 576 = 625.

Suy ra $NP=\sqrt{625}=25$.

b) Từ NP² = MN² + MP², suy ra MP² = NP² ‒ MN² = 29² ‒ 20² = 441.

Suy ra $MP=\sqrt{441}=21$.

c) Từ NP² = MN² + MP², suy ra MN² = NP² ‒ MP² = 61² ‒ 11² = 3600.

Suy ra $MN=\sqrt{3600}=60$.

Bài 2 trang 52 sách bài tập Toán 8 Tập 1: Chứng minh tam giác EFG vuông trong các trường hợp sau:

a) FG = 12, EF = 35, EG = 37;

b) FG = 85, EF = 77, EG = 36;

c) FG = 12, EF = 13, EG = 5.

Lời giải:

a) Ta có EG² = 37² = 1 369 và EF² + FG² = 35² + 12² = 1 369.

Suy ra tam giác EFG vuông tại F (định lí Pythagore đảo).

b) Ta có FG² = 85² = 7 225 và EF² + EG² = 77² + 36² =7 225.

Suy ra tam giác EFG vuông tại E (định lí Pythagore đảo).

c) Ta có EF² = 13² = 169 và EG² + FG² = 12² + 5² = 169.

Suy ra tam giác EFG vuông tại G (định lí Pythagore đảo).

Bài 3 trang 52 sách bài tập Toán 8 Tập 1: Tính chiều cao BH của tam giác ABC cân tại B (Hình 5), biết AB = 9 cm và AC = 4 cm.

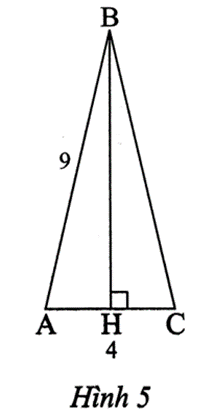
Lời giải:

Tam giác ABC cân tại B nên đường cao BH cũng là đường trung tuyến.

Suy ra $AH=\frac{AC}{2}=\frac{4}{2}=2$ (cm)

Áp dụng định lí Pythagore vào tam giác ABH vuông tại H, ta có:

AB² = AH² + BH²

Suy ra BH² = AB² – AH² = 9² – 2² = 77.

Do đó $BH=\sqrt{77}$(cm).

Bài 4 trang 52 sách bài tập Toán 8 Tập 1: Tính độ dài x trong Hình 6.

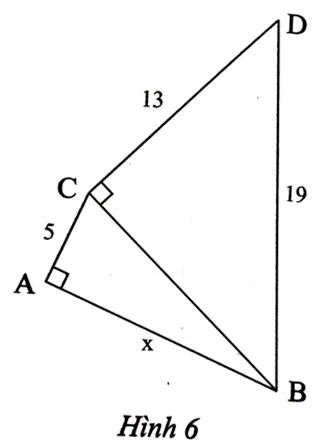
Lời giải:

Áp dụng định lí Pythagore vào tam giác BCD vuông tại C, ta có:

BD² = BC² + CD²

Suy ra: BC² = BD² ‒ CD² = 19² ‒ 13² = 192.

Áp dụng định lí Pythagore vào tam giác ABC vuông tại A, ta có:

BC² = AB² + AC²

Suy ra: AB² = BC² ‒ AC² = 192 ‒ 5² = 167.

Do đó $AB=x=\sqrt{167}$ (cm).

Bài 5 trang 52 sách bài tập Toán 8 Tập 1: Tính độ dài các cạnh chưa biết của tam giác vuông sau:

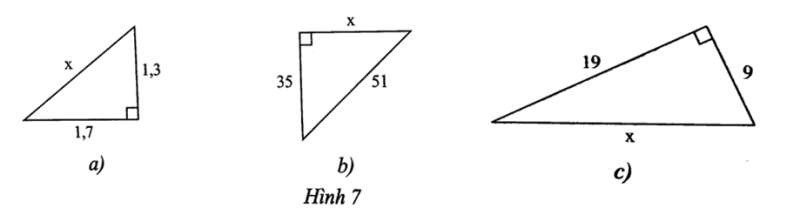
Lời giải:

Áp dụng định lý Pythagore trong tam giác vuông ta có:

a) x² = 1,3² + 1,7² = 4,58

Suy ra: $x=\sqrt{4,58}\approx 2,1$.

b) 51² = 35² + x²

Suy ra x² = 51² – 35² = 1376.

Do đó $x=\sqrt{1376}\approx 37$.

c) x² = 19² + 9² = 442.

Suy ra $x=\sqrt{442}\approx 21$.

Bài 6 trang 52 sách bài tập Toán 8 Tập 1: Tìm tam giác vuông trong các tam giác sau:

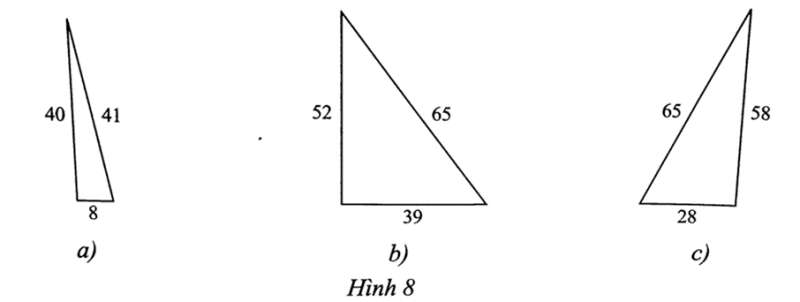
Lời giải:

a) Vì 41² = 1681 ≠ 1664 = 40² + 8² nên Hình 8a không là tam giác vuông.

b) Vì65² = 4225 = 52² + 39² nên theo định lí Pythagore thì Hình 8b là tam giác vuông.

c) Vì65² = 4225 ≠ 4148 = 58² + 28² nên Hình 8c không là tam giác vuông.

Bài tập trang 53 sách bài tập Toán 8 Tập 1

Bài 7 trang 53 sách bài tập Toán 8 Tập 1: Tính khoảng cách x từ đầu thang đến chân tường (Hình 9).

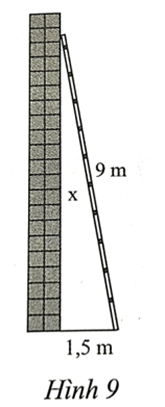
Lời giải:

Khoảng cách x từ đầu thang đến chân tường bằng độ dài cạnh góc vuông trong tam giác vuông nên áp dụng định lý Pythagore trong tam giác vuông ta có:

9² = x² + 5², suy ra $x=\sqrt{9^2-1,5^2}\approx 8,9$ (m).

Bài 8 trang 53 sách bài tập Toán 8 Tập 1: Một máy bay đang ở độ cao 5,2 km. Khoảng cách từ hình chiếu vuông góc của máy bay xuống mặt đất đến vị trí A của sân bay là 10,2 km (Hình 10). Tính khoảng cách từ vị trí máy bay đến vị trí A của sân bay.

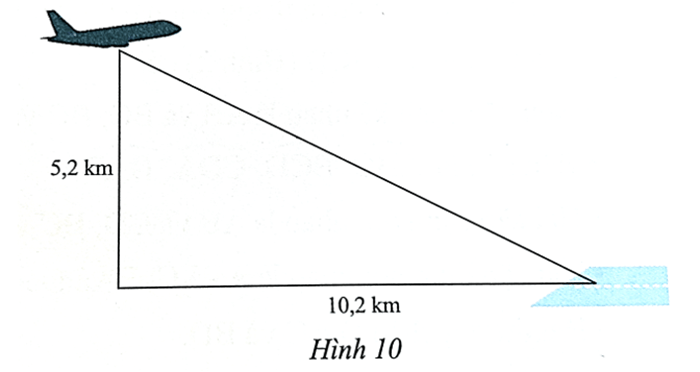
Lời giải:

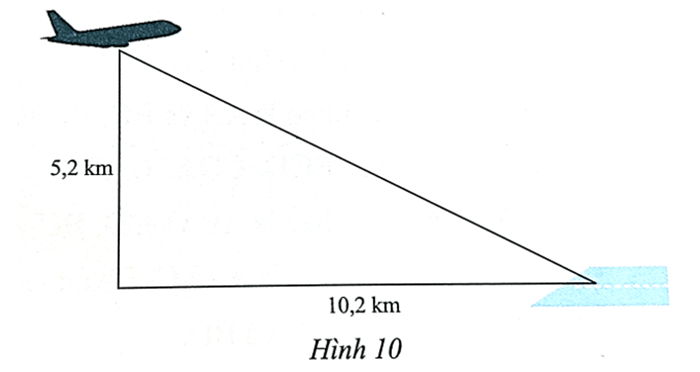
Gọi khoảng cách từ vị trí máy bay đến vị trí A của sân bay là x(km) (x > 0).

Khoảng cách từ vị trí máy bay đến vị trí A của sân bay là độ dài cạnh huyền trong tam giác vuông nên áp dụng định lý Pythagore trong tam giác vuông ta có:

x² = 5,2² + 10,2², suy ra $x=\sqrt{10,2^2+5,2^2}\approx 11,4$ (km).

Vậy khoảng cách từ vị trí máy bay đến vị trí A của sân bay là khoảng 11,4 km.

Xem thêm các bài giải sách bài tậpToán lớp 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Hình chóp tam giác đều

Bài tập cuối chương 2

Bài 2: Tứ giác

Bài 3: Hình thang – Hình thang cân

Bài 5: Hình chữ nhật – Hình vuông