Toptailieu.vn xin giới thiệu Lý thuyết Cấp số nhân (Cánh diều) hay, chi tiết | Lý thuyết Toán 11 Bài viết gồm phần lý thuyết trọng tâm nhất được trình bày một cách dễ hiểu, dễ nhớ bên cạnh đó là bộ câu hỏi trắc nghiệm có hướng dẫn giải chi tiết để học sinh có thể vận dụng ngay lý thuyết, nắm bài một cách hiệu quả nhất. Mời các bạn đón xem:
Lý thuyết Cấp số nhân (Cánh diều) hay, chi tiết | Lý thuyết Toán 11
Bài giải Bài 3: Cấp số nhân
(Nguồn: Sinh học 10, NXB Giáo dục Việt Nam, 2010)
Giả sử lúc đầu có 100 vi khuẩn E. coli.
Hỏi có bao nhiêu vi khuẩn E.coli sau 180 phút?
Lời giải:
Số lượng vi khuẩn lúc đầu Q0 = 100 (vi khuẩn).
Số lượng vi khuẩn sau lần nhân đôi đầu tiên (sau 20 = 1.20 phút) là: Q1 = 100.2 = 200 (vi khuẩn).
Số lượng vi khuẩn sau lần nhân đôi thứ hai (sau 40 = 2.20 phút) là: Q2 = 100.2.2 = 100.22 = 400 (vi khuẩn).
Số lượng vi khuẩn sau lần nhân đôi thứ ba (sau 60 = 3.20 phút) là: Q3 = 100.2.2.2 = 100.23 = 800 (vi khuẩn).
Tổng quát: Số lượng vi khuẩn sau lần nhân đôi thứ n (sau n. 20 phút) là: Qn = 100.2n (vi khuẩn).
Vì vậy số lượng vi khuẩn sau lần nhân đôi thứ thứ 9 (sau 180 = 9.20 phút) là: Q9 = 100.29 = 51 200 (vi khuẩn).
I. Định nghĩa
Lời giải:
Ta có số hạng thứ hai gấp số hạng đứng trước nó 1:=3 lần.
Số hạng thứ ba gấp số hạng đứng trước nó 3:1 = 3 lần.
Số hạng thứ tư gấp số hạng đứng trước nó 9:3 = 3 lần.
Số hạng thứ năm gấp số hạng đứng trước nó 27:9 = 3 lần.
Số hạng thứ sáu gấp số hạng đứng trước nó 81: 27 = 3 lần.
Số hạng thứ bảy gấp số hạng đứng trước nó 243:81 = 3 lần.
Vì vậy ta có kết luận kể từ số hạng thứ hai, ta thấy số hạng sau gấp 3 lần số hạng đứng trước nó.
Luyện tập 1 trang 53 Toán 11 Tập 1: Cho cấp số nhân (un) với u1 = – 6, u2 = – 2.
a) Tìm công bội q.
b) Viết năm số hạng đầu của cấp số nhân đó.
Lời giải:
a) (un) là cấp số nhân có công bội q = .
b) Năm số hạng đầu tiên của dãy cấp số nhân là:
u1 = – 6, u2 = – 2; u3=(-6).; u4=(-6).; u5=(-6)..
Lời giải:
Ta có: un+1 = 3.2n+1
= 2 với n ≥ 1
Vì vậy dãy (un) là cấp số nhân có số hạng đầu u1 = 6 và công bội q = 2.
II. Số hạng tổng quát
Hoạt động 2 trang 54 Toán 11 Tập 1: Cho cấp số nhân (un) có số hạng đầu u1, công bội q.
a) Viết năm số hạng đầu của cấp số nhân theo u1 và q.
b) Dự đoán công thức tính un theo u1 và q.
Lời giải:
a) Năm số hạng đầu của cấp số nhân đã cho là: u1; u1.q; u1.q2; u1q3; u1q4.
b) Dự đoán công thức tính un theo u1 và q là: un = u1qn-1.
Lời giải:
Số tiền ban đầu T1 = 100 (triệu đồng).
Số tiền sau 1 năm bác Linh thu được là:
T2 = 100 + 100.6% = 100.(1 + 6%) (triệu đồng).
Số tiền sau 2 năm bác Linh thu được là:
T3 = 100.(1 + 6%) + 100.(1 + 6%).6% = 100.(1 + 6%)2 (triệu đồng).
Số tiền sau 3 năm bác Linh thu được là:
T4 = 100.(1 + 6%)2 + 100.(1 + 6%)2.6% = 100.(1 + 6%)3 (triệu đồng).
Số tiền sau n năm bác Linh thu được chính là một cấp số nhân với số hạng đầu T1 = 100 và công bội q = 1 + 6% có số hạng tổng quát là:
Tn + 1 = 100.(1 + 6%)n (triệu đồng).
III. Tổng n số hạng đầu của một cấp số nhân
a) Tính Sn.q và Sn – Sn.q.
b) Từ đó, hãy tìm công thức tính Sn theo u1 và q.
Lời giải:
a) Ta có: Sn.q = (u1 + u1q + u1q2 + ... + u1qn-1).q
= u1.q + u1.q2 + u1q3 + ... + u1qn
Sn – Sn.q = u1 + u1q + u1q2 + ... + u1qn-1 – (u1.q + u1.q2 + u1q3 + ... + u1qn)
= u1 – u1qn
b) Ta có:
.
Vậy công thức tính Sn là: .
Luyện tập 4 trang 55 Toán 11 Tập 1: Tính tổng n số hạng đầu của mỗi cấp số nhân sau:
a) 3; – 6; 12; – 24; ... với n = 12;
b) ,... với n = 5.
Lời giải:
a) Ta có: 3; – 6; 12; – 24; ... là cấp số nhân với u1 = 3 và công bội q = – 2.
Khi đó tổng của 12 số hạng đầu của cấp số nhân đã cho là:
= 12 285.
b) Ta có: ,... là một cấp số nhân với u1 = và công bội q=
Khi đó tổng của 5 số hạng đầu của cấp số nhân đã cho là:
= 0,1111.
Bài tập
Bài 1 trang 56 Toán 11 Tập 1: Trong các dãy số sau, dãy số nào là cấp số nhân? Vì sao?
a) 5; – 0,5; 0,05; – 0,005; 0,0005;
b) – 9; 3; – 1; ;
c) 2; 8; 32; 64; 256.
Lời giải:
a) Từ số hạng thứ hai của dãy số ta thấy số hạng sau gấp - lần số hạng trước của dãy.
Vì vậy dãy trên là cấp số nhân với số hạng đầu u1 = 5 và công bội q = – 0,5.
b) Từ số hạng thứ hai của dãy số ta thấy số hạng sau gấp - số hạng trước của dãy.
Vì vậy dãy trên là cấp số nhân với số hạng đầu u1 = – 9 và công bội q= - .
c) Ta có:
Vì vậy dãy trên không là cấp số nhân.
a) ;
b) ;
c) un = ( – 0,75)n.
Lời giải:
a) Ta có:
Xét
Vì vậy dãy số đã cho là một cấp số nhân.
b) Ta có:
Xét .
Vì vậy dãy số đã cho là một cấp số nhân.
c) Ta có: un+1 = (– 0,75)n+1.
Xét .
Vì vậy dãy số đã cho là một cấp số nhân.
Bài 3 trang 56 Toán 11 Tập 1: Cho cấp số nhân (un) với số hạng đầu u1 = – 5, công bội q = 2.
a) Tìm un;
b) Số – 320 là số hạng thứ bao nhiêu của cấp số nhân trên?
c) Số 160 có phải là một số hạng của cấp số nhân trên không?
Lời giải:
a) Ta có (un) là cấp số nhân có số hạng đầu u1 = – 5 và công bội q = 2 có số hạng tổng quát là: un = – 5.2n-1 với mọi n ∈ ℕ*.
b) Xét un = – 5.2n-1 = – 320
⇔ 2n-1 = 64
⇔ n – 1 = 6
⇔ n = 7.
Vậy số – 320 là số hạng thứ 7 của cấp số nhân.
c) Xét un = – 5.2n-1 = 160
⇔ 2n-1 = – 32
⇔ n – 1 = – 5
⇔ n = – 4 ∉ ℕ*
Vậy số 160 không phải là một số hạng của cấp số nhân.
Bài 4 trang 56 Toán 11 Tập 1: Cho cấp số nhân (un) với u1 = 3, .
a) Tìm công bội q và viết năm số hạng đầu của cấp số nhân trên.
b) Tính tổng 10 số hạng đầu của cấp số nhân trên.
Lời giải:
a) Ta có u3 = u1.q2
Xét 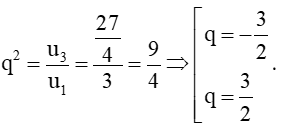
+) Với q = - ta có năm số hạng đầu của cấp số nhân là:
u1 = 3, u2 = 3. ; u3 = ; u4 = 3. ; u5 = 3. .
+) Với q= ta có năm số hạng đầu của cấp số nhân là:
u1 = 3, u2 = 3.; u3 = ;
u4 = 3. ; u5 = 3. .
b) Tổng của 10 số hạng đầu của cấp số nhân với số hạng đầu u1 = 3 và công bội q = - là: -68.
Tổng của 10 số hạng đầu của cấp số nhân với số hạng đầu u1 = 3 và công bội q= là: 340.
a) Viết công thức tính số dân của tỉnh đó sau n năm kể từ năm 2020.
b) Tính số dân của tỉnh đó sau 10 năm kể từ năm 2020.
Lời giải:
a) Ta có dãy (un) lập thành một cấp số nhân có số hạng đầu là u0 = 2 triệu dân và công sai q = 1%.
Khi đó số hạng tổng quát của un = 2.(1 + 1%)n-1 (triệu dân).
b) Số dân của tỉnh đó sau 10 năm kể từ năm 2020 là:
u10 = 2.(1 + 1%)10-1 ≈ 2,19 (triệu dân).
a) Viết công thức tính giá trị của ô tô sau 1 năm, 2 năm sử dụng.
b) Viết công thức tính giá trị của ô tô sau n năm sử dụng.
c) Sau 10 năm, giá trị của ô tô ước tính còn bao nhiêu triệu đồng?
Lời giải:
a) Sau 1 năm giá trị của ô tô còn lại là:
u1 = 800 – 800.4% = 800.(1 – 4%) = 768 (triệu đồng).
Sau 2 năm giá trị của ô tô còn lại là:
u1 = 800.(1 – 4%) – 800.(1 – 4%).4% = 800.(1 – 4%)2 = 737,28 (triệu đồng).
b) Gọi un là giá trị của ô tô sau n năm sử dụng.
Dãy số (un) tạo thành một cấp số nhân với số hạng đầu là giá trị đầu của ô tô là u0 = 800 triệu đồng và công bội q = 1 – 4%.
Khi đó công thức tổng quát để tính un = 800.(1 – 4%)n.
c) Sau 10 năm sử dụng giá trị của ô tô còn lại là:
u10 = 800.(1 – 4%)10 ≈ 531,87 (triệu đồng).
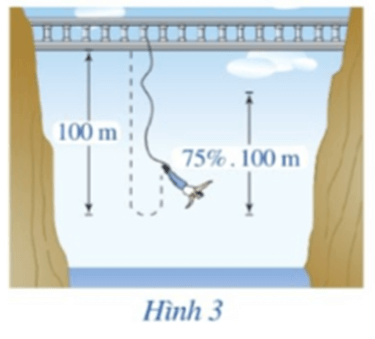
Lời giải:
Gọi un là độ dài dây kéo sau n lần rơi xuống (n ∈ ℕ)
Ta có: u0 = 100 (m).
Sau lần rơi đầu tiên độ dài dây kéo còn lại là: u1 = 100.75% (m).
Sau cú nhảy tiếp theo độ dài dây kéo còn lại là: u2 = 100.75%.75% = 100.(75%)2 (m).
...
Dãy số này lập thành một cấp số nhân có số hạng đầu là 100 và công bội q = 0,75%, có công thức tổng quát un = 100.(0,75%)n-1 (m).
Tổng quãng đường người đó đi được sau 10 lần kéo lên và lại rơi xuống là:
377,5 (m).
Xem thêm các bài giải sách giáo khoa Toán 11 Cánh Dều hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.