Toptailieu.vn giới thiệu Vở bài tập Toán 8 trang 148, 149, 150, 151, 152, 153, 154 Phần đại số – Ôn tập cuối năm chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong Vở bài tập Toán 8. Mời các bạn đón đọc.
Vở bài tập Toán 8 trang 148, 149, 150, 151, 152, 153, 154 Phần hình học – Ôn tập cuối năm
Vở bài tập Toán 8 trang 148 - 154 Bài 1: Rút gọn rồi tính giá trị của biểu thức sau tại :
Phương pháp giải:
- Qui đồng cùng mẫu thức rồi rút gọn biểu thức.
- Thay giá trị tương ứng của vào biểu thức sau khi đã rút gọn để tính giá trị của biểu thức đó.
Lời giải:
Biểu thức đã cho có dạng
Ta có:
Vậy
Tại thì:
Vở bài tập Toán 8 trang 148 - 154 Bài 2: Chứng minh rằng:
Phương pháp giải:
Ta chứng minh hiệu hai vế bằng .
Sử dụng hằng đẳng thức số 3:
Lời giải:
Xét hiệu hai vế:
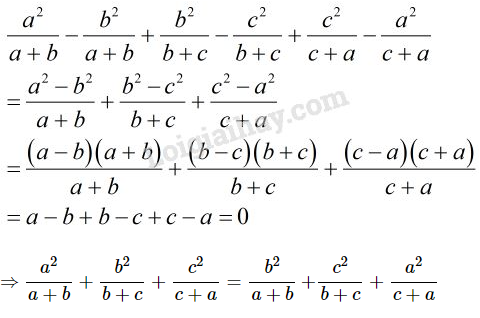
Lưu ý:
Có thể giải bằng cách biến đổi từ vế trái sang vế phải như sau:
=
Vở bài tập Toán 8 trang 148 - 154 Bài 3: Tìm các giá trị nguyên của để phân thức có giá trị là một số nguyên:
Phương pháp giải: Để nguyên thì tử số phải chia hết cho mẫu số.
Lời giải:
Thực hiện phép chia đa thức ta có:
nguyên thì nguyên. Do đó, để M có giá trị nguyên thì phải là ước của
+) (thỏa mãn đk)
+) (thỏa mãn đk)
+) (thỏa mãn đk)
+) (thỏa mãn đk)
Vậy các giá trị nguyên cần tìm là:
Vở bài tập Toán 8 trang 148 - 154 Bài 4: Giải các phương trình:
a,
b,
Phương pháp giải:
a,
Áp dụng bài toán: |A(x)| = B(x)
với
hoặc với
b,
Áp dụng bài toán: |A(x)| = B(x)
với
hoặc với
Lời giải:
a,
Vậy
b,
Vậy
Vở bài tập Toán 8 trang 148 - 154 Bài 5: Giải phương trình:
Phương pháp giải: Cộng hai vế với 2, biến đổi để xuất hiện nhân tử chung sau đó đưa về dạng phương trình tích.
Lời giải:
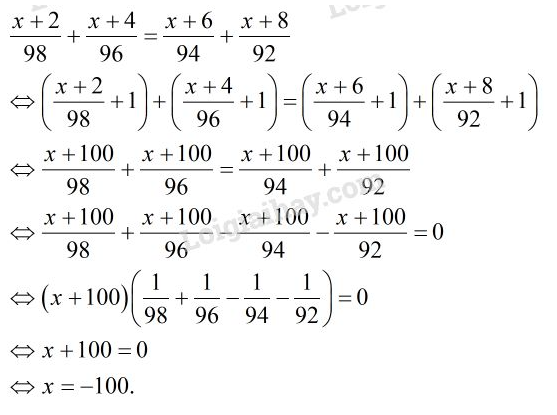
Vì:
Vậy phương trình có nghiệm
Vở bài tập Toán 8 trang 148 - 154 Bài 6: Giải các phương trình:
a,
b,
Phương pháp giải:
a,
- Tìm điều kiện xác định.
- Qui đồng khử mẫu.
- Rút gọn rồi tìm nghiệm .
- Đối chiếu với điều kiện xác định rồi kết luận nghiệm.
b,
- Tìm điều kiện xác định.
- Qui đồng khử mẫu.
- Rút gọn rồi tìm nghiệm .
- Đối chiếu với điều kiện xác định rồi kết luận nghiệm.
Lời giải:
a,
Vậy phương trình đã cho vô nghiệm hay
b,
Vậy phương trình có nghiệm là bất cứ số nào khác hay
Vở bài tập Toán 8 trang 148 - 154 Bài 7: Giải các phương trình:
a,
b,
Phương pháp giải:
a,
- Biến đổi phương trình về dạng phương trình tích.
- Tìm
- Kết luận
b,
- Tìm điều kiện xác định.
- Qui đồng khử mẫu.
- Rút gọn rồi tìm nghiệm .
- Đối chiếu với điều kiện xác định rồi kết luận nghiệm.
Lời giải:
a,
Vậy
b,
Vậy
Vở bài tập Toán 8 trang 148 - 154 Bài 8: Một xí nghiệp dự định sản xuất sản phẩm trong ngày. Nhưng nhờ tổ chức lao động hợp lí nên thực tế đã sản xuất mỗi ngày vượt sản phẩm. Do đó xí nghiệp đã sản xuất không những vượt mức dự định sản phẩm mà còn hoàn thành trước thời hạn. Hỏi thực tế xí nghiệp đã rút ngắn được bao nhiêu ngày?
Phương pháp giải:
- Bước 1: Đặt số ngày rút bớt làm ẩn, biểu diễn các đại lượng còn lại theo ẩn.
- Bước 2: Từ điều kiện của để bài lập phương trình biểu diễn mối quan hệ giữa các đại lượng.
- Bước 3: Tìm ẩn.
- Bước 4: Kết luận.
Lời giải:
Gọi (ngày) là thời gian thực tế xí nghiệp đã rút ngắn được ()
Số ngày sản xuất thực tế của xí nghiệp là (ngày)
Số sản phẩn đã sản xuất được là: (sản phẩm)
Số sản phẩm dự định sản xuất mỗi ngày là (sản phẩm).
Số sản phẩm thực tế sản xuất được mỗi ngày là:
(sản phẩm)
Vì mỗi ngày vượt 15 sản phẩm so với dự định nên ta có phương trình :
Giải phương trình trên ta được:
thỏa mãn điều kiện
Vậy thực tế xí nghiệp đã rút ngắn được ngày.
Đáp số: 3 ngày
Vở bài tập Toán 8 trang 148 - 154 Bài 9: Cho biểu thức:
a) Rút gọn biểu thức .
b) Tính giá trị của tại , biết .
c) Tìm giá trị của để .
Phương pháp giải:
a) Tìm ĐKXĐ, tìm mẫu thức chung sau đó qui đồng và rút gọn biểu thức.
b)
Thay giá trị tương ứng của x vào biểu thức đã được rút gọn rồi tính giá trị của biểu thức đó.
c) Giải bất phương trình với vế trái là biểu thức vế phải là
Lời giải:
ĐKXĐ:
a)
b)
+) Tại (tmđk) thì
+) Tại (tmđk) thì
c) (tmđk)
Vậy thì
Vở bài tập Toán 8 trang 148 - 154 Bài 10: Giải bất phương trình:
Phương pháp giải:
- Bước 1: Chuyển tất cả các hạng tử sang vế trái.
- Bước 2: Qui đồng cùng mẫu thức chung.
- Bước 3: Rút gọn, tìm nghiệm của bất phương trình.
- Bước 4: Kết luận
Lời giải:
Điều kiện xác định:
Vậy .