Với giải SGK Toán 11 Chân trời sáng tạo trang 127 chi tiết trong Bài tập cuối chương 4 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải Toán 11 trang 127 Tập 1 (Chân trời sáng tạo)

Bài 1 trang 127 Toán 11 Tập 1: Cho tam giác ABC. Lấy điểm M trên cạnh AC kéo dài (Hình 1). Mệnh đề nào sau đây là mệnh đề sai?

A. M ∈ (ABC);

B. C ∈ (ABM);

C. A ∈ (MBC);

D. B ∈ (ACM).

Lời giải:

Đáp án đúng là: A

Ta có: M ∈ AC ⊂ (ABC).

Bài 2 trang 127 Toán 11 Tập 1: Cho tứ diện ABCD với I và J lần lượt là trung điểm các cạnh AB và CD. Mệnh đề nào sau đây đúng?

A. Bốn điểm I, J, B, C đồng phẳng;

B. Bốn điểm I, J, A, C đồng phẳng;

C. Bốn điểm I, J, B, D đồng phẳng;

D. Bốn điểm I, J, C, D đồng phẳng.

Lời giải:

Đáp án đúng là: D

Bài 3 trang 127 Toán 11 Tập 1: Cho hình chóp SABCD có AC cắt BD tại M, AB cắt CD tại N. Trong các đường thẳng sau đây, đường nào là giao tuyến của (SAC) và (SBD)?

A. SM;

B. SN;

C. SB;

D. SC.

Lời giải:

Đáp án đúng là: A

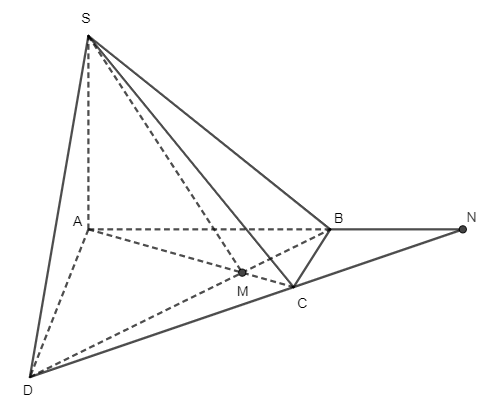
Ta có: S ∈ (SAC) ∩ (SBD)

M ∈ AC ⊂ (SAC)

M ∈ BD ⊂ (SBD)

⇒ M ∈ (SAC) ∩ (SBD)

Vậy (SAC) ∩ (SBD) = SM.

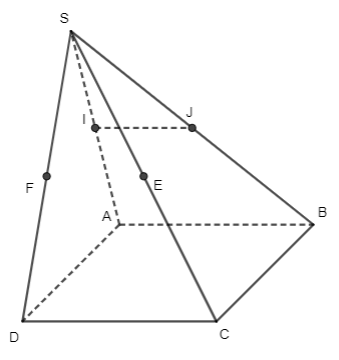
Bài 4 trang 127 Toán 11 Tập 1: Cho hình chóp SABCD có đáy ABCD là hình bình hành. Gọi I, J, E, F lần lượt là trung điểm SA, SB, SC, SD. Trong các đường thẳng sau, đường nào không song song với IJ?

A. EF;

B. DC;

C. AD;

D. AB.

Lời giải:

Đáp án đúng là: C

+) Trong tam giác SAB, có: IJ // AB (IJ là đường trung bình của tam giác)

Ta lại có AB // DC nên IJ // DC

+) Trong tam giác SDC có EF // DC (EF là đường trung bình của tam giác)

+) AD với IJ là hai đường thẳng chéo nhau.

Bài 5 trang 127 Toán 11 Tập 1: Cho hình bình hành ABCD và một điểm S không nằm trong mặt phẳng (ABCD). Giao tuyến của hai mặt phẳng (SAB) và (SCD) là một đường thẳng song song với đường thẳng nào sau đây?

A. AB;

B. AC;

C. BC;

D. SA.

Lời giải:

Đáp án đúng là: A

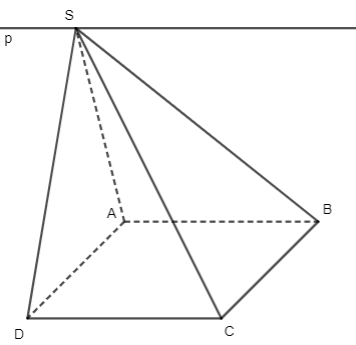
Ta có: AB // CD

AB ⊂ (SAB)

CD ⊂ (SCD)

S ∈ (SAB) ∩ (SCD)

Suy ra giao tuyến của (SAB) và (SCD) đường thẳng p đi qua S song song với AB và CD.

Bài 6 trang 127 Toán 11 Tập 1: Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng 10. M là điểm trên SA sao cho $\frac{SM}{SA}=\frac{2}{3}$. Một mặt phẳng (α) đi qua M song song với AB và CD, cắt hình chóp theo một tứ giác có diện tích là:

A. $\frac{400}{9}$;

B. $\frac{200}{3}$;

C. $\frac{40}{9}$;

D. $\frac{200}{9}$.

Lời giải:

Đáp án đúng là: A

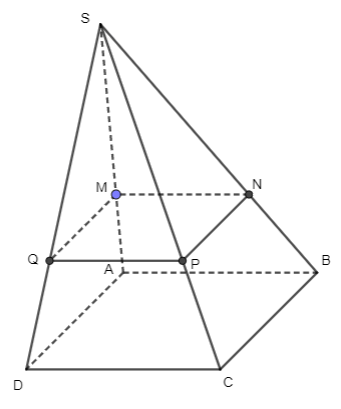
+) Trong mặt phẳng (SAB), từ M kẻ đường thẳng song song với AB cắt SB tại N.

Suy ra giao tuyến của (α) với (SAB) là MN.

+) Trong mặt phẳng (SBC), từ N kẻ đường thẳng song song với BC // AD cắt SC tại P.

Suy ra giao tuyến của (α) với (SBC) là NP.

+) Trong mặt phẳng (SAD), từ điểm M kẻ đường thẳng song song với AD cắt SD tại Q.

Suy ra giao tuyến của (α) với (SAD) là MQ.

Do đó mặt phẳng (MNPQ) là mặt phẳng (α) cần dựng.

Ta có MNPQ là hình vuông có cạnh bằng $\frac{2}{3}$ cạnh hình vuông và bằng $\frac{20}{3}$.

Diện tích của MNPQ là: ${\left(\frac{20}{3}\right)}^2=\frac{400}{9}$ (đvdt).

Bài 7 trang 127 Toán 11 Tập 1: Quan hệ song song trong không gian có tính chất nào trong các tính chất sau?

A. Nếu hai mặt phẳng (P) và (Q) song song với nhau thì mọi đường thẳng nằm trong (P) đều song song với (Q).

B. Nếu hai mặt phẳng (P) và (Q) song song với nhau thì mọi đường thẳng nằm trong (P) đều song song với mọi đường thẳng nằm trong (Q).

C. Nếu hai đường thẳng song song với nhau lần lượt nằm trong hai mặt phẳng phân biệt (P) và (Q) thì (P) và (Q) song song với nhau.

D. Qua một điểm nằm ngoài mặt phẳng cho trước ta vẽ được một và chỉ một đường thẳng song song với mặt phẳng cho trước đó.

Lời giải:

Đáp án đúng là: D

Qua một điểm nằm ngoài mặt phắng cho trước ta vẽ được nhiều hơn một đường thẳng song song với mặt phẳng cho trước đó