Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Số vô tỉ và khái niệm cơ bản về căn bậc hai (50 bài tập minh họa) hay, chi tiết nhất, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về hỗn số, từ đó học tốt môn Toán 7.
Phương pháp giải Số vô tỉ và khái niệm cơ bản về căn bậc hai (50 bài tập minh họa)
I. LÝ THUYẾT:
1. Số vô tỉ:
- Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn.
- Tập hợp các số vô tỉ được kí hiệu là I.
2. Khái niệm về căn bậc hai:
- Căn bậc hai của một số a không âm là số x sao cho x2 = a.
- Số dương a có đúng hai căn bậc hai là và .
Số 0 chỉ có một căn bậc hai là số 0: = 0.
II. CÁC DẠNG BÀI TẬP CƠ BẢN:
Dạng 9.1: Liên hệ giữa lũy thừa bậc hai và căn bậc hai.
1. Phương pháp giải:
Nếu x2 = a thì = x và ngược lại.
(Lũy thừa bậc hai và căn bậc hai của một số không âm là hai phép toán ngược nhau).
2. Ví dụ minh họa:
Ví dụ 1: Theo mẫu: Vì 22 = 4 nên , hãy hoàn thành bài tập sau:
a) Vì 32 = … nên = 3
b) Vì 4… = 16 nên … = 4
c) Vì 102 = … nên … = …
Giải:
a) Vì 32 = 9 nên = 3
b) Vì 42 = 16 nên = 4
c) Vì 102 = 100 nên = 10
Dạng 9.2: Tìm căn bậc hai của một số cho trước.
1. Phương pháp giải:
- Sử dụng định nghĩa của căn bậc hai.
- Lưu ý: Số dương có hai căn bậc hai là hai số đối nhau; số âm không có căn bậc hai.
- Khi viết ta phải có và
- Có thể sử dụng máy tính bỏ túi (nút dấu căn bậc hai).
2. Ví dụ minh họa:
Ví dụ 4: Tính:
a) b) c)
Giải:
a) = 9 (vì 9 > 0 và 92 = 81)
b) = –8 (vì – 8 < 0 và (–8)2 = 64)
c) = 7 (vì 7 > 0 và 72 = 49)
Dạng 9.3: Tìm một số biết căn bậc hai của nó.
1. Phương pháp giải:
Nếu thì x = a2
2. Ví dụ minh họa:
Ví dụ 3: Tìm giá trị của x2 trong các trường hợp sau:
a) Nếu = 3 thì x2 = ?
b) Nếu = 5 thì x2 = ?
Giải:
a) Vì = 3 nên x = 32 = 9, do đó x2 = 92 = 81.
b) Vì = 5 nên x = 52 = 25, do đó x2 = 252 = 625.
III. BÀI TẬP VẬN DỤNG:
Bài 1: Điền các kí hiệu thích hợp vào dấu ...:
![]()
Bài 2: Trong các số sau, số nào thuộc là số hữu tỉ, số nào là số vô tỉ?
![]()
Bài 3: Biết và . Sắp xếp các số x, y, z theo thứ tự tăng dần.
Bài 4: So sánh các số sau:
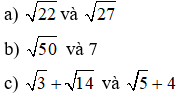
Bài 5: Tìm tổng các giá trị của x thỏa mãn: (2x – 1)2 = 3
Bài 6: Tìm , biết:
a) x2 = 4 b) x2 = 5 c) (2x – 1)2 = 16
Bài 7: Tính bằng cách hợp lý:
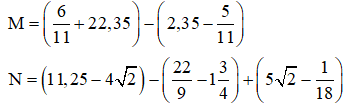
Bài 8: So sánh:
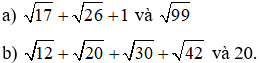
Bài 9: Cho . Tìm số nguyên x để A có giá trị là một số nguyên.
Bài 10: Tìm giá trị lớn nhất của biểu thức B=
Hướng dẫn giải:
Bài 1:
a) b) c) d)
Bài 2: Đáp án:
Số vô tỉ:
![]()
Bài 3: x < y < z
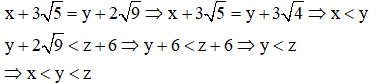
Bài 4:
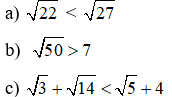
Bài 5:
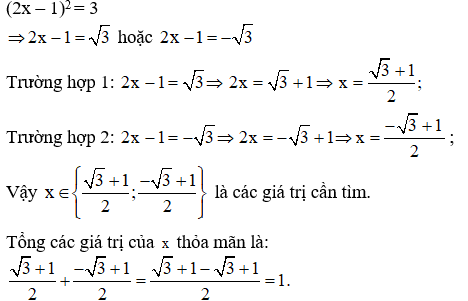
Bài 6:
a)
b) Không tồn tại x hữu tỉ thỏa mãn.
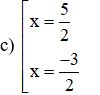
Bài 7: Đáp án:
a) 21
b)
Bài 8:
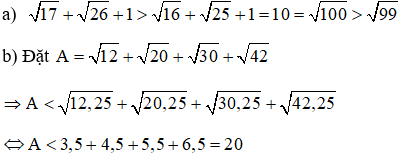
Bài 9:

Bài 10:
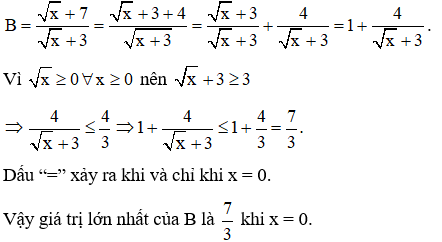
Xem thêm các dạng Toán 7 hay, chọn lọc khác:
Cách làm tròn số và cách giải các dạng bài tập
Các dạng bài tập về Số thực và cách giải
Công thức tính giá trị tuyệt đối của một số hữu tỉ
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.