Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Cách làm tròn số và cách giải các dạng bài tập (50 bài tập minh họa) hay, chi tiết nhất, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về hỗn số, từ đó học tốt môn Toán 7.

Phương pháp giải Cách làm tròn số và cách giải các dạng bài tập (50 bài tập minh họa)

I. LÝ THUYẾT:

Quy ước làm tròn số:

Trường hợp 1. Nếu chữ số đầu tiên trong các chữ số bị bỏ đi nhỏ hơn 5 thì ta giữ nguyên bộ phận còn lại. Trong trường hợp số nguyên thì ta thay các chữ số bị bỏ đi bằng các chữ số 0.

Trường hợp 2. Nếu chữ số đầu tiên trong các chữ số bị bỏ đi lớn hơn hoặc bằng 5 thì ta cộng thêm 1 vào chữ số cuối cùng của bộ phận còn lại. Trong trường hợp số nguyên thì ta thay các chữ số bị bỏ đi bằng các chữ số 0.

II. CÁC DẠNG BÀI TẬP CƠ BẢN:

Dạng 8.1: Làm tròn các số theo một yêu cầu cho trước.

1. Phương pháp giải:

- Áp dụng quy ước làm tròn số trong hai trường hợp.

- Chú ý hiểu đúng các cụm từ “làm tròn số đến chữ số thập phân thứ…”,

“làm tròn chữ số đến hàng…”.

2. Ví dụ minh họa:

Ví dụ 1:

a) Làm tròn số 23,1826 đến chữ số thập phân thứ ba;

b) Làm tròn số 23,1826 đến chữ số thập phân thứ hai;

c) Làm tròn số 23,1826 đến chữ số thập phân thứ nhất.

Giải

a) 23,1826 $\approx$  23,183 (chữ số bỏ đi là 6 > 5).

b) 23,1826 $\approx$  23,18 (chữ số bỏ đi là 2 < 5).

c) 23,1826 $\approx$  23,2 (chữ số bỏ đi là 8 > 5).

Dạng 8.2: Giải bài toán rồi làm tròn kết quả.

1. Phương pháp giải:

Căn cứ vào đề bài, giải bài toán rồi làm tròn kết quả theo yêu cầu của đề bài. Chú ý đề bài yêu cầu “làm tròn đến chữ số thập phân thứ…” hoặc “làm tròn đến chữ số hang…”.

2. Ví dụ minh họa:

Ví dụ 2: Hết học kì I, điểm Toán của bạn An như sau:

Hệ số 1: 6 ; 8 ; 5 ; 9.

Hệ số 2: 7 ; 6 ; 8 ; 9.

Hệ số 3: 7.

Tìm điểm trung bình môn Toán học kì I của bạn An (làm tròn đến chữ số thập phân thứ nhất).

Giải:

Điểm trung bình môn Toán học kì I của bạn An là:

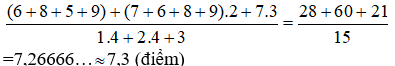
Vậy điểm trung bình môn Toán học kì I của bạn An là 7,3 điểm.

Dạng 8.3: Áp dụng quy ước làm tròn số để ước lượng kết quả các phép tính.

1. Phương pháp giải:

Để ước lượng kết quả các phép tính, ta thường áp dụng quy ước làm tròn số để làm tròn chữ số ở hàng cao nhất của mỗi số tham gia vào phép tính.

Ví dụ: Số 7329 được làm tròn số đến chữ số ở hàng cao nhất là $\approx$ 7000.

2. Ví dụ minh họa:

Ví dụ 3: Hãy ước lượng kết quả các phép tính sau:

a) 128.42                                                     b) 6921: 49

Giải:

a) 128.42 $\approx$  130.40 = 5200.

Tích phải tìm có 4 chữ số và xấp xỉ 5200.

b) 6921: 49 $\approx$  7000 : 50 = 140.

Thương phải tìm có 3 chữ số và xấp xỉ 140.

III. BÀI TẬP VẬN DỤNG:

Bài 1: Làm tròn các số sau đây: 7842; 89367; 917527; 17493

a. Đến hàng trăm.

b. Đến hàng nghìn.

Bài 2: Tính trung bình cộng của các số 7; 5; 11 rồi làm tròn đến chữ số thập phân thứ ba.

Bài 3: Thực hiện phép tính rồi làm tròn kết quả đến chữ số thập phân thứ hai:

a) 4,5672 + 2,34 + 0,167

b) (2,364 + 8,2) – (7,002 + 0,17)

c) 78,2.4,006

Bài 4: Tổng kết năm học, bạn Ngân được điểm như sau: Toán: 7,8; Văn: 8,3; Lí: 7,0; Tiếng Anh: 7,5; Sử: 8,5; Địa: 9,0. Tính điểm trung bình các môn học của bạn Ngân (làm tròn kết quả đến chữ số thập phân thứ nhất).

Bài 5: Viết các phân số sau thành số thập phân, rồi làm tròn lần lượt các số đó đến chữ số thập phân thứ hai: $\frac{8}{33};\frac{26}{111};\frac{5}{24};\frac{15}{82}$

Bài 6: Một tam giác có cạnh đáy bằng $\frac{13}{2}cm$ . Cạnh đáy dài gấp rưỡi độ dài đường cao tương ứng và 1cm. Tính diện tích tam giác đó (làm tròn đến hàng đơn vị)

Bài 7: Làm tròn các số đến hàng đơn vị rồi tính kết quả của phép tính:

a) (0,93 + 1,72)(8,5 – 1,7)

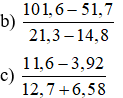
d) (4,62 + 21,7).4,21

Bài 8: Tính giá trị của biểu thức rồi làm tròn đến hàng đơn vị:

A = (9,126 : 0.65).718 + 1,45.28,20

$B=\frac{\left(11,81+8,19\right).2,25}{7,65}$

C = 50,93.49.49.15 – 59,83.29,21

Bài 9: Ba phân số tối giản có tổng bằng $3\frac{7}{60}$, các tử số của chúng tỉ lệ với 2 : 3 : 5, các mẫu của chúng tỉ lệ với 5 : 4 : 6. Đưa phân số này về dạng số thập phân và làm tròn đến chữ số thập phân thứ ba.

Bài 10: Tìm x, làm tròn x đến số thập phân thứ ba:

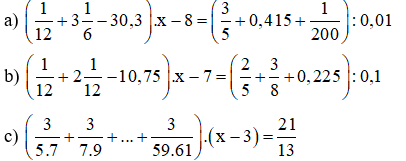
Hướng dẫn giải:

Bài 1:

a) Làm tròn đến chữ số hàng trăm: 7800; 89400; 917500; 17500.

b) Làm tròn đến chữ số hàng nghìn: 8000; 89000; 918000; 17000.

Bài 2:

Trung bình cộng của ba số 7; 5; 11 là: $\frac{7+5+11}{3}=7,66666...\approx 7,667$

Bài 3:

a) 11,3392 $\approx$ 11,34

b) 3,392 $\approx$ 3,39

c) 313,2692 $\approx$ 313,27

Bài 4:

Bài 5:

Bài 6:

Độ dài đường cao của tam giác là:$\frac{13}{2}:\frac{3}{2}-1=\frac{10}{3}\left(cm\right)$ .

Diện tích tam giác là: $\frac{1}{2}.\frac{13}{2}.\frac{10}{3}=\frac{130}{12}=10,8333...\approx 11\left(c{m}^2\right)$

Bài 7:

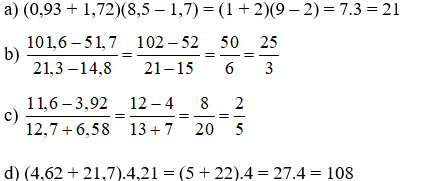
Bài 8: Đáp án:

A = 142

B = 6

C = 2

Bài 9: 

Bài 10: Tìm x, làm tròn x đến số thập phân thứ ba:

a) x $\approx$ – 4,067

b) x $\approx$ – 1,981

c) x $\approx$ – 8,865

Xem thêm các dạng Toán 7 hay, chọn lọc khác:

Cách giải bài tập Số thập phân hữu hạn, số thập phân vô hạn tuần hoàn

Số vô tỉ và khái niệm cơ bản về căn bậc hai và cách giải

Các dạng bài tập về Số thực và cách giải

Công thức tính giá trị tuyệt đối của một số hữu tỉ

Công thức lũy thừa của số hữu tỉ