Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Cách giải bài tập Số thập phân hữu hạn, số thập phân vô hạn tuần hoàn (50 bài tập minh họa) hay, chi tiết nhất, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về hỗn số, từ đó học tốt môn Toán 7.

Phương pháp giải Cách giải bài tập Số thập phân hữu hạn, số thập phân vô hạn tuần hoàn (50 bài tập minh họa)

I. LÝ THUYẾT:

- Nếu một phân số tối giản với mẫu dương mà mẫu không có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân hữu hạn.

- Nếu một phân số tối giản với mẫu dương mà mẫu có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân vô hạn tuần hoàn.

- Mỗi số hữu tỉ được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoàn. Ngược lại, mỗi số thập phân hữu hạn hoặc vô hạn tuần hoàn biểu diễn một số hữu tỉ.

II. CÁC DẠNG BÀI TẬP CƠ BẢN:

Dạng 7.1: Nhận biết một phân số viết được dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.

1. Phương pháp giải:

- Viết phân số dưới dạng phân số tối giản với mẫu dương.

- Phân tích mẫu dương đó ra thừa số nguyên tố.

- Nhận xét:

+ Nếu mẫu này không có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân hữu hạn.

+ Nếu mẫu này có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân vô hạn tuần hoàn.

2. Ví dụ minh họa:

Ví dụ 1: Trong hai phân số sau, phân số nào viết được dưới dạng số thập phân hữu hạn, phận số nào viết được dưới dạng số thập phân vô hạn tuần hoàn?

$\frac{55}{-300};\frac{63}{-360}$

Giải:  

Dạng 7.2: Viết một tỉ số hoặc một phân số dưới dạng số thập phân.

1. Phương pháp giải:

Để viết một tỉ số hoặc một phân số $\frac{a}{b}$ dưới dạng số thập phân ta làm phép chia a : b.

2. Ví dụ minh họa:

Ví dụ 2: Dùng dấu ngoặc để chỉ rõ chu kì trong thương (viết dưới dạng số thập phân vô hạn tuần hoàn) của các phép chia sau:

a) 4,15 : 3                       b) 8,75 : 6                                 c) 15,23 : 11

Giải:

a) 4,15 : 3 = 1,38333… = 1,38(3).

b) 8,75 : 6 = 1,41666… = 1,41(6).

c) 15,23 : 11 = 1,38454545… = 1,38(45).

Dạng 7.3: Viết số thập phân hữu hạn dạng phân số tối giản.

1. Phương pháp giải:

- Viết số thập phân hữu hạn dưới dạng một phân số có tử là số nguyên tạo bởi phần nguyên và phần thập phân của số đó, mẫu là một lũy thừa của 10 với số mũ bằng số chữ số ở phần thập phân của số đã cho.

- Rút gọn phân số nói trên.

2. Ví dụ minh họa:

Ví dụ 3: Viết các số thập phân hữu hạn sau đây dưới dạng phân số tối giản:

a) 0,42                            b) 0,125                                   c) –8,12     

Giải:

a) 0,42 = $\frac{42}{100}=\frac{21}{50}$

b) 0,125 = $\frac{125}{1000}=\frac{1}{8}$

c) –8,12 = $\frac{-812}{100}=\frac{-203}{25}$

Dạng 7.4: Viết số thập phân vô hạn tuần hoàn dưới dạng phân số tối giản.

1. Phương pháp giải:

Để giải dạng toán này cần có kiến thức bổ sung sau đây:

Số thập phân vô hạn tuần hoàn gọi là đơn nếu chu kì bắt đầu ngay sau dấu phẩy. Phần thập phân đứng trước chu kỳ gọi là phần bất thường.

Người ta đã chứng minh được các quy tắc sau:

a) Muốn viết phần thập phân của số thập phân vô hạn tuần hoàn đơn dưới dạng phân số, ta lấy chu kì làm tử, còn mẫu là một số gồm các chữ số 9, số chữ số 9 bằng số chữ số của chu kì.

b) Muốn viết phần thập phân của số thập vô hạn tuần hoàn tạp dưới dạng phân số, ta lấy số gồm phần bất thường và chu kì trừ đi phần bất thường làm tử, còn mẫu là một số gồm các chữ số 0 bằng số chữ số của phần bất thường.

2. Ví dụ minh họa:

Ví dụ 4: Hai số 0,(45) và 0,4(54) có bằng nhau không ?

Giải:

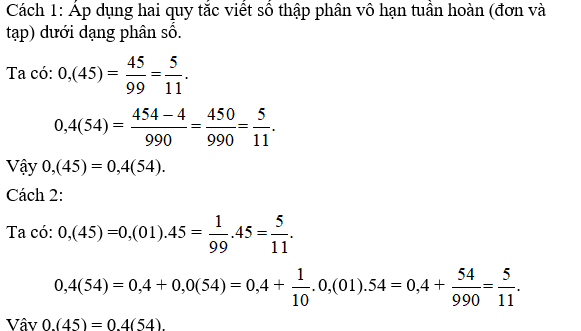
III. BÀI TẬP VẬN DỤNG:

Bài 1: Giải thích vì sao các phân số sau viết được dưới dạng số thập phân hữu hạn rồi viết chúng dưới dạng đó: $\frac{-5}{32};\frac{7}{125};\frac{13}{80};\frac{-21}{50}$

Bài 2: Trong các số sau, số nào viết được dưới dạng số thập phân hữu hạn? Giải thích? Biểu diễn các số đó dưới dạng số thập phân hữu hạn hoặc số thập phân vô hạn.

Bài 3: Viết các phân số sau đây dưới dạng số thập phân vô hạn tuần hoàn, chỉ rõ chu kì sau đó sắp xếp các phân số theo chiều tăng dần của chu kì.

Bài 4: Giải thích vì sao các phân số sau viết được dưới dạng số thập phân hữu hạn rồi viết chúng dưới dạng đó:

$\frac{-5}{32};\frac{7}{125};\frac{13}{20};\frac{-21}{50}$

Bài 5: Viết các số thập phân vô hạn tuần hoàn sau dưới dạng phân số tối giản:

a) 0,2(3)                                   b) 1,4(51)            

c) 0,(31)                                   d) –3,24(41)

Bài 6: Tìm x, biết:

a) 0,(37).x + 1,2(32) = 1

b) 0,(26).x = 1,2(31)

Bài 7:Tìm số tự nhiên x < 100 sao cho phân số $\frac{x+2}{105}$ viết được dưới dạng số thập phân hữu hạn.

Bài 8: Tính:

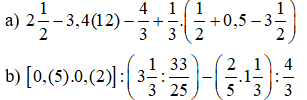
Bài 9: Tìm ba phân số có tổng bằng $1\frac{37}{44}$ , các tử của chúng tỉ lệ với 4:3:5; các mẫu số của chúng tỉ lệ với 1:2:4. Chứng tỏ rằng các phân số này viết được dưới dạng số thập phân vô hạn tuần hoàn rồi viết dạng thập phân của chúng.

Bài 10: Tính:

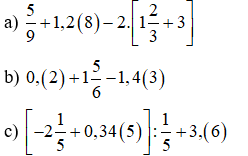
Hướng dẫn giải:

Bài 1: Vì mẫu số của các phân số chỉ có các ước là 2 và 5.

Bài 2:

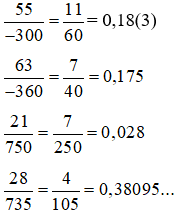
Bài 3:

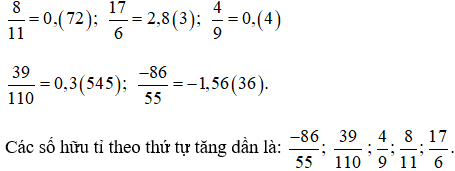
Bài 4:

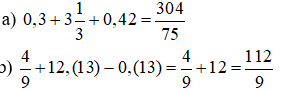
Bài 5:

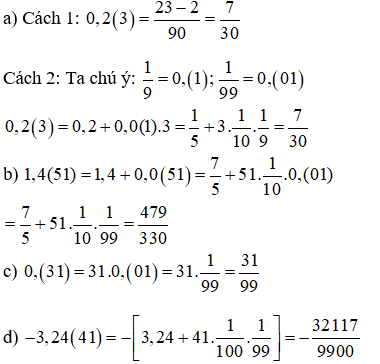
Bài 6:

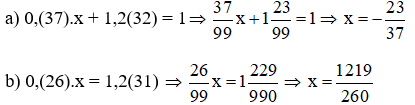
Bài 7:

Ta có 105 = 3.5.7

Vậy $\frac{x+2}{105}$ phân số viết được dưới dạng số thập phân hữu hạn khi (x+2) $⋮21$ .

Từ đó, x có thể là các giá trị {19; 40; 61; 82}

Bài 8:

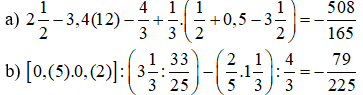
Bài 9:

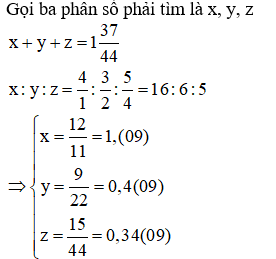
Bài 10:

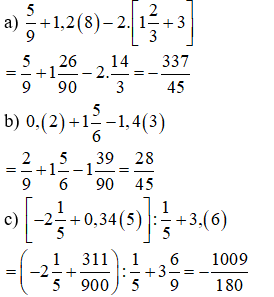
Xem thêm các dạng Toán 7 hay, chọn lọc khác:

Các dạng toán về Tính chất của dãy tỉ số bằng nhau và cách giải

Cách làm tròn số và cách giải các dạng bài tập

Số vô tỉ và khái niệm cơ bản về căn bậc hai và cách giải

Các dạng bài tập về Số thực và cách giải

Công thức tính giá trị tuyệt đối của một số hữu tỉ