Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Các dạng toán về Tính chất của dãy tỉ số bằng nhau (50 bài tập minh họa) hay, chi tiết nhất, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về hỗn số, từ đó học tốt môn Toán 7.
Phương pháp giải Các dạng toán về Tính chất của dãy tỉ số bằng nhau (50 bài tập minh họa)
I. LÝ THUYẾT:
1. Tính chất của dãy tỉ số bằng nhau:

2. Khi nói các số x, y, z tỉ lệ với các số a, b, c tức là ta có xa=yb=zc
Ta cũng viết: x : y : z = a : b : c.
II. CÁC DẠNG BÀI TẬP CƠ BẢN:
Dạng 6.1: Thay tỉ số giữa các số hữu tỉ bằng tỉ số giữa các số nguyên.
1. Phương pháp giải:
- Viết các số hữu tỉ dưới dạng phân số.
- Thực hiện phép chia phân số.
2. Ví dụ minh họa:
Ví dụ 1: Thay tỉ số giữa các số hữu tỉ bằng tỉ số giữa các số nguyên:
2,05 : 1,2
Giải:
Ta có: 2,05 : 1,2 = 4120:65=4120.56=4124
Vậy tỉ số giữa hai số hữu tỉ 2,05 : 1,2 bằng tỉ số giữa hai số nguyên 41: 24
Dạng 6.2: Tìm hai số biết tổng (hoặc hiệu) và tỉ số của chúng.
1. Phương pháp giải:
Để tìm hai số x và y biết tổng x + y = s hoặc hiệu x – y = d và tỉ số xy=ab
ta làm như sau xy=ab => xa=yb
Áp dụng tính chất của dãy tỉ số bằng nhau:
![]()
![]()
2. Ví dụ minh họa:
Ví dụ 2: Tìm x, y biết:
a) x + y =60 và x9=y11
b) y – x = 24 và x4=y7
Giải:
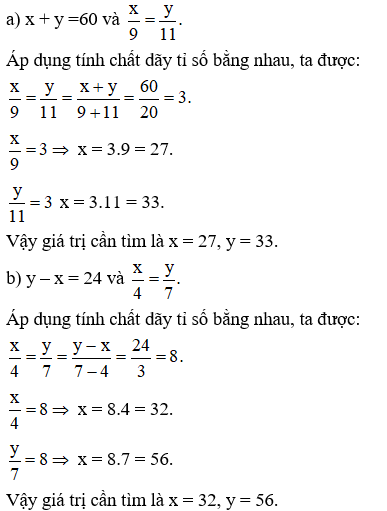
Dạng 6.3: Chia một số thành các phần tỉ lệ với các số cho trước.
1. Phương pháp giải:
Giả sử phải chia số S thành ba phần x, y, z tỉ lệ với các số a, b, c. Ta làm như sau: xa=yb=zc=x+y+za+b+c=Sa+b+c
Do đó,
![]()
2. Ví dụ minh họa:
Ví dụ 4: Các cạnh của một tam giác có độ dài tỉ lệ với các số 3; 5; 7. Tính độ dài mỗi cạnh của tam giác, biết chu vi của nó bằng 40,5 cm.
Giải:
Gọi độ dài các cạnh của tam giác lần lượt là a, b, c (cm, 0 < a, b, c < 40,5).

Vậy độ dài ba cạnh của tam giác lần lượt là 8,1 cm; 13,5 cm; 18,9 cm.
Dạng 6.5: Tìm hai số biết tích và tỉ số của chúng.
1. Phương pháp giải:
Giả sử phải tìm hai số x, y biết x.y = P và xy=ab
Đặt xa=ya=k , ta có x = k.a, y = k.b.
Do đó x.y = (k.a).(k.b) = k2.ab = P => k2=Pab
Từ đó tìm được k rồi suy ra x và y.
2. Ví dụ minh họa:
Ví dụ 5: Tìm hai số x và y, biết rằng:
x3=y4 và xy = 48.
Giải:
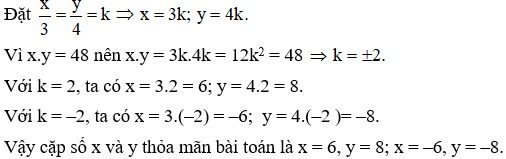
Dạng 6.6: Chứng minh đẳng thức từ một tỉ lệ thức cho trước.
1. Phương pháp giải:
Cho tỷ lệ thức ab=cd Cần chứng minh tỷ lệ thức xy=mn theo k, ta thường làm các phương pháp sau:
Phương pháp 1. Chứng tỏ rằng: ad = bc.
Phương pháp 2: Đặt k là giá trị chung của ab;cd Tính xy;mn theo k.
Phương pháp 3: Dùng biến đổi đại số và tính chất của dãy tỷ số bằng nhau để từ tỷ lệ thức đã cho biến đổi dần thành tỷ lệ thức phải chứng minh.
2. Ví dụ minh họa:
Ví dụ 6: Cho a, b, c, d khác 0 từ tỷ lệ thức: ab=cd Chứng minh:
a)a-ba=c-dc
b)(a-bc-d)2=abcd
Giải:

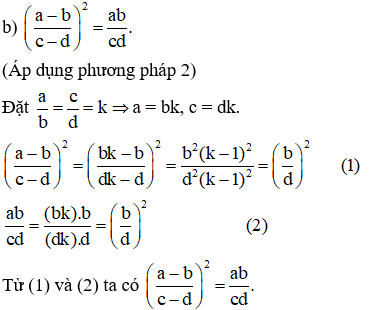
III. BÀI TẬP VẬN DỤNG:
Bài 1: Tìm x, y biết:
a) x9=y11 và x + y =60
b)x4=y7 và y – x = 24
Bài 2:Tìm các số x, y, z biết:
a) –x + y – z = 11 và 9x = 5y = 15z.
![]()
Bài 3: Tìm diện tích của một hình chữ nhật có tỉ số giữa hai cạnh của nó bằng 23 và chu vi bằng 40cm.
Bài 4: Các cạnh của một tam giác có số đo tỉ lệ với các số 3, 5, 7. Tính mỗi cạnh của tam giác, biết chu vi của nó bằng 40,5 cm.
Bài 5:Tìm x, y, z trong mỗi trường hợp sau:
a) x3=y12=x5 và xyz = 0,225.
b) x2=y3=z5 và xyz = 810
Bài 6: Cho ab=bc=ca. Chứng minh rằng: a = b = c
Bài 7: Tìm hai phân số tối giản biết tổng của chúng là 2936 , các tử số theo thứ tự tỉ lệ với 7 và 5; các mẫu số theo thứ tự tỉ lệ với 3 và 2.
Bài 8: Ba lớp 7 có tất cả 153 học sinh. Số học sinh lớp 7B bằng 89 số học sinh lớp 7A. Số học sinh lớp 7C bằng 1716 số học sinh lớp 7B. Tính số học sinh của mỗi lớp.
Bài 9: Cho a, b, c, d là các số hữu tỉ dương và ab=cd .
Chứng minh rằng: (a + 2c) (b + d) = (a + c) (b + 2d)
Bài 10: Cho ab=bc=cd . Chứng minh rằng: (a+b+cb+c+d)3=ad .
Hướng dẫn giải:
Bài 1: Đáp án:
a) x = 27; y = 33
b) x = 32, y =56.
Bài 2:
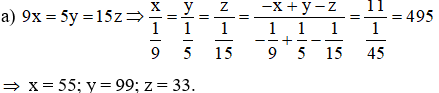
b) x = 112; y = 78; z = 152.
Bài 3:
Gọi chiều rộng, chiều dài là x, y
Ta cóx2=y3;2x+2y=40
=>x=8;y=12
Diện tích hình chữ nhật là: 8.12 = 96 (cm2)
Bài 4:
Gọi các cạnh của tam giác lần lượt là a, b, c
Ta có a3=b5=c7=a+b+c15=40,515=2,7
Suy ra a, b, c lần lượt là 8,1; 13,5; 18,9 (cm)
Bài 5:
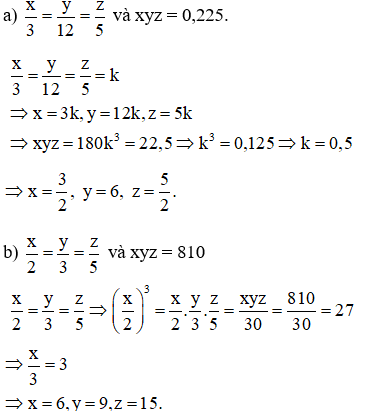
Bài 6: Áp dụng tính chất của tỉ lệ thức:
ab=bc=ca=a+b+cb+c+a=1
=> a=b=c=1
Bài 7: Gọi hai phân số cần tìm là x, y.
Từ giả thiết ta có: x:y=73:52=14:15 .
Hai phân số là: x=718;y = 512
Bài 8: Gọi số học sinh lớp 7A, 7B, 7C lần lượt là: a, b, c (0 < a, b, c < 153)
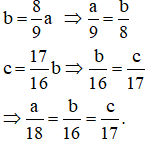
Từ đó tính được: a = 54, b = 48, c = 51.
Bài 9:
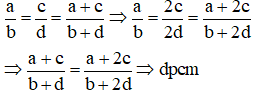
Bài 10:
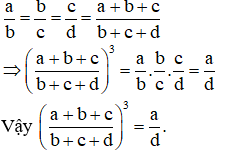
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.