Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Các dạng toán về Tỉ lệ thức (50 bài tập minh họa) hay, chi tiết nhất, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về hỗn số, từ đó học tốt môn Toán 7.

Phương pháp giải Các dạng toán về Tỉ lệ thức (50 bài tập minh họa)

I. LÝ THUYẾT:

1. Định nghĩa:

Tỉ lệ thức là đẳng thức của hai tỉ số $\frac{a}{b}=\frac{c}{d}$ .

Hay được viết: a:b=c:d . Trong đó a, d là các số hạng ngoài (ngoại tỉ), b, c là các số hạng trong (trung tỉ).

2. Tính chất:

Tính chất 1: Nếu $\frac{a}{b}=\frac{c}{d}$ thì ad = bc.

Tính chất 2: Nếu ad = bc và a, b, c, d ≠ 0 thì ta có các tỉ lệ thức:

II. CÁC DẠNG BÀI TẬP CƠ BẢN:

Dạng 5.1: Thay tỉ số giữa các số hữu tỉ bằng tỉ số giữa các số nguyên.

1. Phương pháp giải:

- Viết các số hữa tỉ dưới dạng phân số.

- Thực hiện phép chia phân số.

2. Ví dụ minh họa:

Ví dụ 1: Thay tỉ số giữa các số hữu tỉ bằng tỉ số giữa các số nguyên.

a) 0,26 : 0,65

b)$3\frac{1}{3}:10$

Giải:

a) Ta có: 0,26 : 0,65 = $\frac{26}{100}:\frac{65}{100}=\frac{26}{100}.\frac{100}{65}=\frac{2}{5}$

Vậy tỉ số giữa hai số hữu tỉ 0,26 : 0,65 bằng tỉ số giữa hai số nguyên 2 : 5.

b) Ta có:$3\frac{1}{3}:10=\frac{10}{3}:\frac{10}{1}=\frac{10}{3}.\frac{1}{10}=\frac{1}{3}$

Vậy tỉ số giữa hai số hữu tỉ $3\frac{1}{3}:10$ bằng tỉ số giữa hai số nguyên 1:3.

Dạng 5.2: Lập tỉ lệ thức từ các tỉ số cho trước.

1. Phương pháp giải:

- Xét xem hai tỉ số đã cho co bằng nhau không?

- Nếu hai tỉ số bằng nhau thì chúng lập thành một tỉ lệ thức.

2. Ví dụ minh họa:

Ví dụ 2: Các tỉ số sau đây có lập thành một tỉ lệ thức hay không?

$\frac{3}{5}:6$và$\frac{4}{5}:8$

Giải:

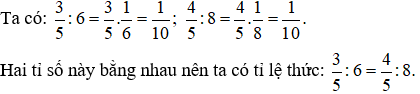
Dạng 5.3: Lập tỉ lệ thức từ đẳng thức cho trước, từ một tỉ lệ thức cho trước, từ các số cho trước.

1. Phương pháp giải:

Lập tỉ lệ thức từ đẳng thức cho trước:

Nếu ad = bc và abcd ≠ 0 thì ta có các tỉ lệ thức:

Lập tất cả các tỉ lệ thức từ một tỉ lệ thức cho trước:

Từ tỉ lệ thức $\frac{a}{b}=\frac{c}{d}$ ta có thể lập được ba tỉ lệ thức nữa bằng cách:

- Giữ nguyên ngoại tỉ, đổi chỗ các trung tỉ: $\frac{a}{c}=\frac{b}{d}$

- Giữ nguyên trung tỉ, đổi chỗ các ngoại tỉ: $\frac{d}{b}=\frac{c}{a}$

- Đổi chỗ các ngoại tỉ với nhau, các trung tỉ với nhau: $\frac{d}{c}=\frac{b}{a}$

Lập tỉ lệ thức từ các số cho trước: Từ các số đã cho, trước hết phải lập được đẳng thức dạng ad = bc. Sau khi có đẳng thức này, áp dụng tính chất 2 để lập các tỉ lệ thức.

2. Ví dụ minh họa:

Ví dụ 3: Lập tất cả các tỉ lệ thức có thể được từ các đẳng thức sau:

2,3.4,5 = 1,5.6,9

Giải:

Các tỉ lệ thức có thể được từ các đẳng thức 2,3.4,5 = 1,5.6,9 là:

Dạng 5.4: Tìm số hạng chưa biết của một tỉ lệ thức.

1. Phương pháp giải:

Trong một tỉ lệ thức, ta có thể tìm một số hạng chưa biết khi biết ba số hạng kia.

2. Ví dụ minh họa:

Ví dụ 4: Tìm x trong các tỉ lệ thức sau:

a) $\frac{2,5}{7,5}=\frac{x}{0,6}$                                       

b)$3\frac{4}{5}:40\frac{8}{15}=0,25:x$                                                               

Giải:

III. BÀI TẬP VẬN DỤNG:

Bài 1: Lập tất cả các tỉ lệ thức có thể có từ các đẳng thức sau:

a)  12.20 = 15.16

b) $\frac{-5}{15}=\frac{-1,2}{3,6}$ 

c) 2,4.3,2  = 8.0,96  

Bài 2: Các tỉ số sau đây có lập thành một tỉ lệ thức hay không? Giải thích.

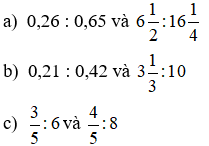
Bài 3: Lập tất cả các tỉ lệ thức từ 4 số sau:  0,25; 1,25; 12; 60.

Bài 4: Lập tất cả các tỉ lệ thức có thể được từ 4 trong 5 số sau:

a) 2; 8; 32; 128; 512

b) 1; 5; 25; 125; 625

Bài 5: Tìm x trong các tỉ lệ thức:

a) 2,5:7,5= x: $\frac{3}{5}$

b) x : 2,5 = 0,003 : 0,75

c) $\frac{5}{6}:x=20:3$

Bài 6: Tìm số hữu tỉ x trong tỉ lệ thức:

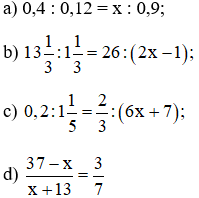
Bài 7: Cho tỉ lệ thức $\frac{3x-y}{x+y}=\frac{3}{4}$. Tìm giá trị của tỉ số $\frac{x}{y}$ .

Bài 8: Bộ bốn số nào dưới đây có thể lập thành một tỉ lệ thức?

a)  $46\frac{1}{2};60\frac{3}{5};77\frac{1}{2}$và 101;

b) $\frac{-1}{8};\frac{5}{6};-4,5$  và 31,5.

c) (1 + 2 + 3)²; (1 + 2 + 3)³; 1³ +  2³ + 3³  và 1³. 2³. 3³

Bài 9: Biết rằng $\frac{t}{x}=\frac{4}{3};\frac{z}{x}=\frac{1}{6}$ . Tìm tỉ số:$\frac{t}{z}$.

Bài 10: Tính  $\frac{a+b}{c+b}$, khi biết $\frac{b}{a}=2$ và $\frac{c}{b}=3$

Hướng dẫn giải:

Bài 1: Các cặp tỉ lệ thức lập được từ các đẳng thức là:

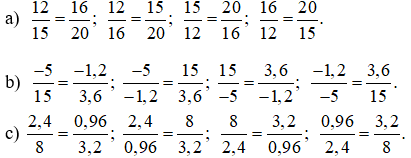
Bài 2: Đáp án:

a) Có vì 0,26:0,65=$6\frac{1}{2}:16\frac{1}{4}$

b) Không.

c) Có vì $\frac{3}{5}:6=\frac{4}{5}:8$

Bài 3: Ta có: 0,25.60 = 1,25.12.

Từ đó suy ra các tỉ lệ thức:

Bài 4: Các cặp tỉ lệ từ 4 trong số là:

a) 2.512 = 8.128

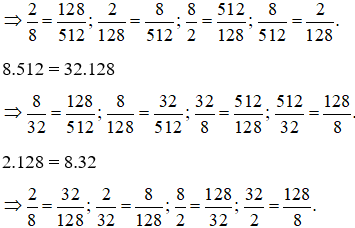
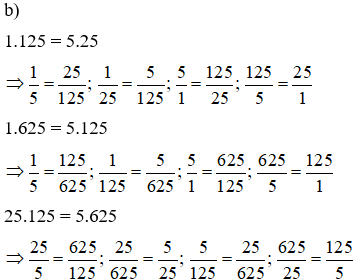
Bài 5:

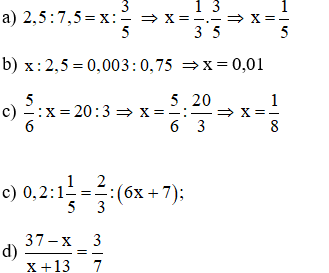
 Bài 6: Đáp án:

a) x = 3                                                        b) $x=\frac{9}{5}$

c)$x=\frac{-1}{2}$                                                                 d) x = 22

Bài 7:

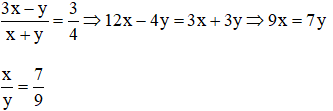
Bài 8:

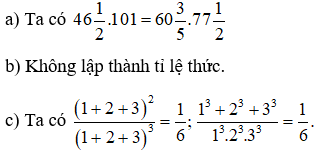
Bài 9:

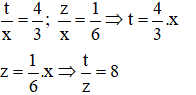
Bài 10:

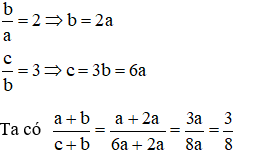
Xem thêm các dạng Toán 7 hay, chọn lọc khác:

Các dạng toán về Lũy thừa của số hữu tỉ và cách giải

Các dạng toán về Tính chất của dãy tỉ số bằng nhau và cách giải

Cách giải bài tập Số thập phân hữu hạn, số thập phân vô hạn tuần hoàn

Cách làm tròn số và cách giải các dạng bài tập

Số vô tỉ và khái niệm cơ bản về căn bậc hai và cách giải