Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Các dạng toán về Lũy thừa của số hữu tỉ (50 bài tập minh họa) hay, chi tiết nhất, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về hỗn số, từ đó học tốt môn Toán 7.
Phương pháp giải Các dạng toán về Lũy thừa của số hữu tỉ (50 bài tập minh họa)
I. LÝ THUYẾT:
1. Lũy thừa với số mũ tự nhiên:
Lũy thừa bậc n của một số hữa tỉ x, kí hiệu xn, là tích của n thừa số x (n là một số tự nhiên lớn hơn 1):
![]()
Nếu thì
Quy ước: x1 = x; x0 = 1 (x ≠ 0).
2. Tích và thương của hai lũy thừa cùng cơ số:
(Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng hai số mũ).
(Khi chia hai lũy thừa cùng cơ số khác 0, ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi số mũ của lũy thừa chia).
3. Lũy thừa của một tích:
(Lũy thừa của một tích bằng tích các lũy thừa)
4. Lũy thừa của một thương:
(y ≠ 0) (Lũy thừa của một thương bằng thương các lũy thừa).
5. Lũy thừa của lũy thừa:
(Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ)
II. CÁC DẠNG BÀI TẬP CƠ BẢN:
Dạng 4.1: Sử dụng định nghĩa của lũy thừa với số mũ tự nhiên.
1. Phương pháp giải:
Nắm vững định nghĩa:
![]()
Quy ước: x1 = x; x0 = 1 (x ≠ 0)
2. Ví dụ minh họa:
Ví dụ 1: Tính:

Giải:
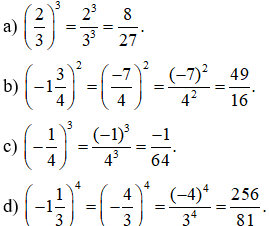
Dạng 4.2: Tính tích và thương của hai lũy thừa cùng cơ số.
1. Phương pháp giải:
Áp dụng các công thức tính tích và thương của hai lũy thừa cùng cơ số.
2. Ví dụ minh họa:
Ví dụ 2: Tìm x, biết:
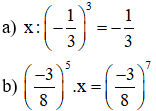
Giải:
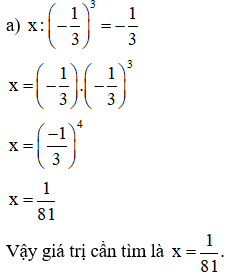
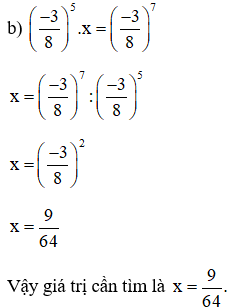
Dạng 4.3: Tính lũy thừa của một lũy thừa:
1. Phương pháp giải:
Áp dụng các công thức tính lũy thừa của một lũy thừa: (xm)n = xm.n.
Chú ý:
- Trong nhiều trường hợp ta phải sử dụng công thức này theo chiều từ phải sang trái: xm.n = (xm)n = (xn)m.
- Tránh sai lầm do lẫn lộn hai công thức: xm.xn = xm+n và (xm)n = xm.n
2. Ví dụ minh họa:
Ví dụ 3:
a) Viết các số và dưới dạng các lũy thừa có số mũ là 8.
b) Trong hai số và số nào lớn hơn?
Giải:
a) Nhận xét: 24 = 8.3; 16 = 8.2. Ta có:
224 = 23.8 = (23)8
316 = 32.8 = (32)8
a) Vì 23 < 32 nên (23)8 < (32)8.
Vậy 316 > 224.
Dạng 4.4: Tính lũy thừa của một tích, lũy thừa của một thương.
1. Phương pháp giải:
Áp dụng các công thức:
(Lũy thừa của một tích bằng tích các lũy thừa)
(Lũy thừa của một thương bằng thương các lũy thừa).
2. Ví dụ minh họa:
Ví dụ 4: Viết các biểu thức sau dưới dạng lũy thừa của một số hữu tỉ:
a) (0,125)3.512 b)
Giải:
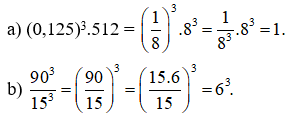
Dạng 5.5: Tìm số mũ của một lũy thừa.
1. Phương pháp giải:
Khi giải bài toán này, ta có thể sử dụng tính chất sau đây:
Với a ≠ 0, a ≠ 1, nếu am = an thì m = n.
2. Ví dụ minh họa:
Ví dụ 5: Tìm số tự nhiên n biết:
Giải:
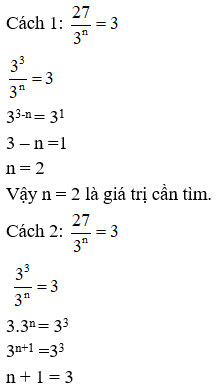
n = 2
Vậy n = 2 là giá trị cần tìm.
Dạng 5.6: Tìm cơ số của một lũy thừa.
1. Phương pháp giải:
- Sử dụng định nghĩa của lũy thừa với số số mũ nguyên dương:
![]()
- Sử dụng tính chất: Nếu an = bn thì a = b nếu b lẻ, a = b nếu b chẵn
2. Ví dụ minh họa:
Ví dụ 6: Tìm x, biết:
a) x3 = 64 b) (x – 5)2 = x – 5
Giải:
a) x3 = 64
Ta có: 64 = 43. Do đó x3 = 43 nên x = 4.
Vậy x = 4 là giá trị cần tìm.
b) (x – 5)2 = x – 5.
Nếu x = 5, ta có 02 = 0 (đúng).
Nếu x ≠ 5, chia hai vế cho (x – 5) ≠ 0, ta được: x – 5 = 1=> x = 6.
Vậy có hai giá trị cần tìm là x = 5 hoặc x = 6.
Dạng 1.7: Tìm giá trị của biểu thức.
1. Phương pháp giải:
- Cần thực hiện đúng thứ tự của các phép tính:
+ Nếu phép tính có chứa cộng, trừ, nhân, chia và nâng lên lũy thì ta thực hiện nâng lên lũy thừa trước rồi đến nhân, chia và cuối cùng là cộng, trừ.
+ Nếu phép tính có dấu ngoặc cần làm theo thứ tự: ngoặc tròn rồi đến ngoặc vuông và sau đó là ngoặc nhọn.
- Áp dụng các quy tắc của các phép tính và các tính chất của các phép tính đó.
2. Ví dụ minh họa:
Ví dụ 7: Tính:

Giải:
![]()
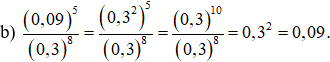
III. BÀI TẬP VẬN DỤNG:
Bài 1: Viết các số sau đây dưới dạng lũy thừa của một số hữu tỉ:
Bài 2: Tính:

Bài 3: Viết các tích sau đây dưới dạng lũy thừa:
a) 2.16.8 b) 25.5.125 c)
Bài 4: Tính

Bài 5: Tìm x, biết:
a)
b)
Bài 6: Tính giá trị của các biểu thức:

Bài 7: Viết các biểu thức sau đây dưới dạng lũy thừa của một số hữu tỉ:
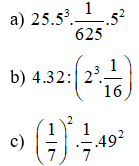
Bài 8: Tìm các số nguyên x, biết:
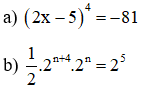
Bài 9: So sánh:
a) 1020 và 910
b) 68 và 1612
c) và
Bài 10: Chứng minh rằng:
a) (76 + 75 – 74) 55
b) (165 + 215) 33
Hướng dẫn giải:
Bài 1: Các số sau đây dưới dạng lũy thừa của một số hữu tỉ là:
Bài 2:
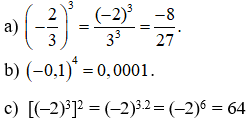
d)
Bài 3:
a) 2.16.8 = 2.24.23 = 28
b) 25.5.125 = 52.5.53 = 56
c)
Bài 4:
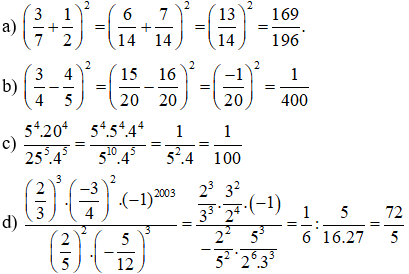
Bài 5: Tìm x, biết:
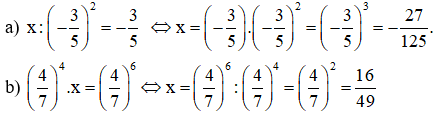
Bài 6: Tính giá trị của các biểu thức:
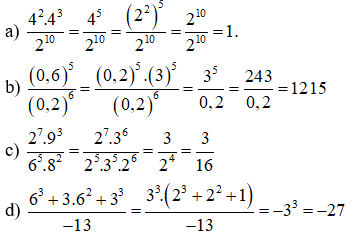
Bài 7: Viết các biểu thức sau đây dưới dạng lũy thừa của một số hữu tỉ:
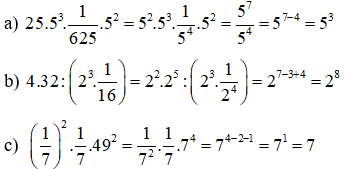
Bài 8:
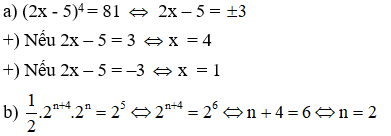
Bài 9: So sánh:
a) 1020 = (102)10 = 10100 > 910
b) 648 và 1612
648 = (26)8 = 248
1612 = (24)12 = 248
648 = 1612
c)
Bài 10: Đưa các lũy thừa về cùng cơ số, sau đó đặt nhân tử chung và chứng minh.
a) (76 + 75 – 74) = 74.(72 + 7 – 1) 55
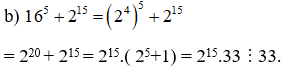
Xem thêm các dạng Toán 7 hay, chọn lọc khác:
Cách giải bài tập Cộng, trừ, nhân, chia số hữu tỉ cơ bản và nâng cao
Giá trị tuyệt đối của một số hữu tỉ và cách giải
Các dạng toán về Tỉ lệ thức và cách giải
Các dạng toán về Tính chất của dãy tỉ số bằng nhau và cách giải
Cách giải bài tập Số thập phân hữu hạn, số thập phân vô hạn tuần hoàn
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.